配对样本T检验

# 1、作用

配对样本 T 检验用于比较配对的连续变量 X1 与连续变量 X2 之间的差异情况，同时要求配对变量差值呈现正态性分布。
​

# 2、输入输出描述

输入：样本数相同，且差值呈现正态分布的两个定量变量。
输出：这两个定量变量是否存在差异性。
​

# 3、案例示例

示例：检验某医院 300 个病人注射某药剂前后血压是否一致。
​

# 4、案例数据

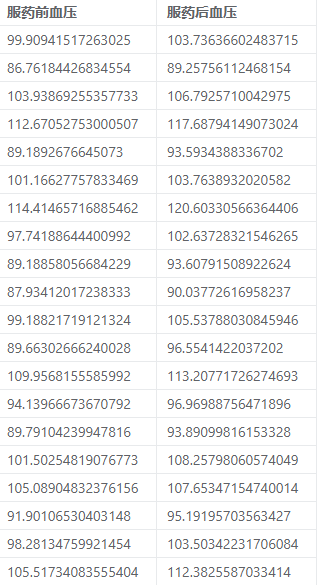
配对样本t检验案例数据

# 5、案例操作

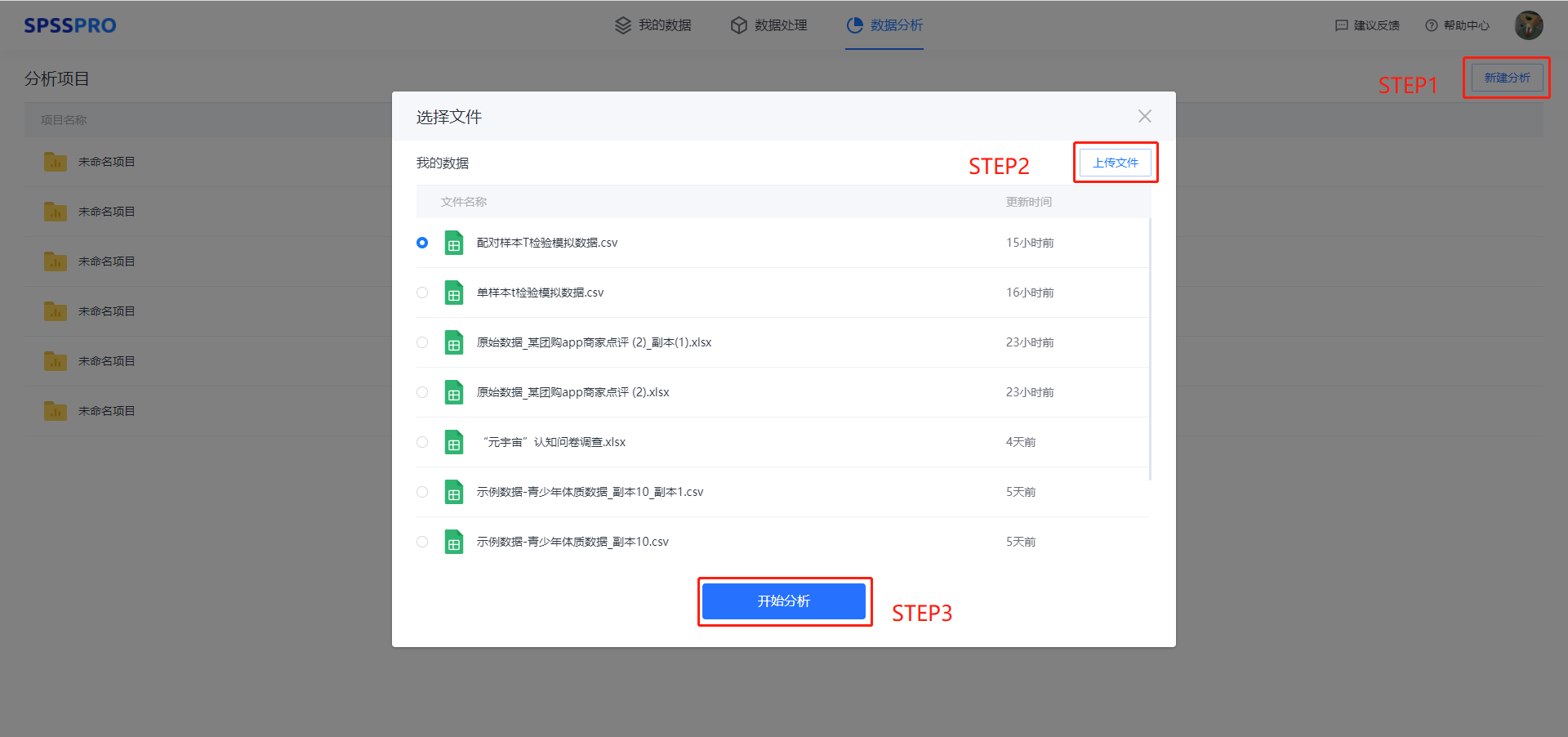
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

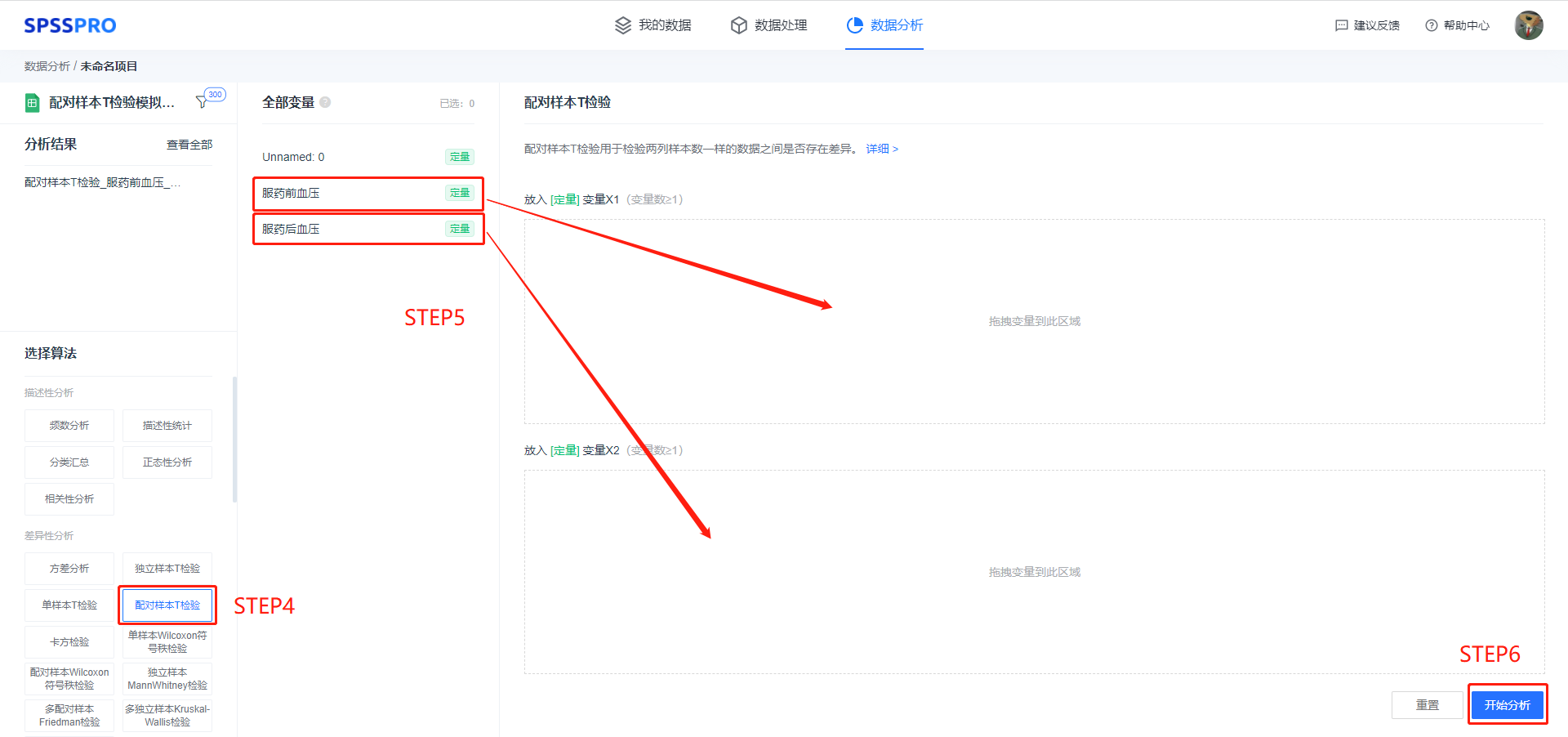
step4：选择【配对样本T检验】；
step5：查看对应的数据数据格式，【配对样本T检验】分组项要求输入数据为定量变量，且至少有一项；
step6：点击【开始分析】，完成全部操作；
​

# 6、输出结果分析

输出结果 1：正态性检验结果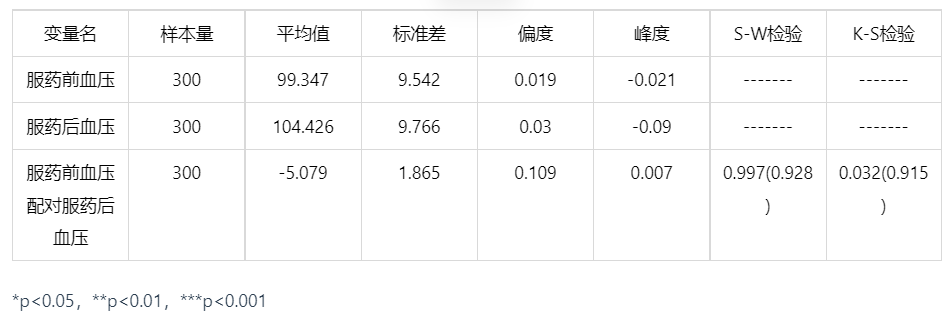

图表说明：
因为配对样本需要满足正态性故在此进行正态性检验，服药前血压配对服药后血压样本数量 N≥5000，采用 K-S 检验，显著性 P 值为 0.915，水平上不呈现显著性，不能拒绝原假设，因此数据不满足正态分布，可根据正态性检验直方图进一步检验是否具有正态性，若不具有正态性可采用非参数检验的 Wilcoxon 符号秩检验、Nemenyi 检验方法。
其峰度（0.007）绝对值小于 10 并且偏度（0.109）绝对值小于 3。

输出结果 2：正态性检验直方图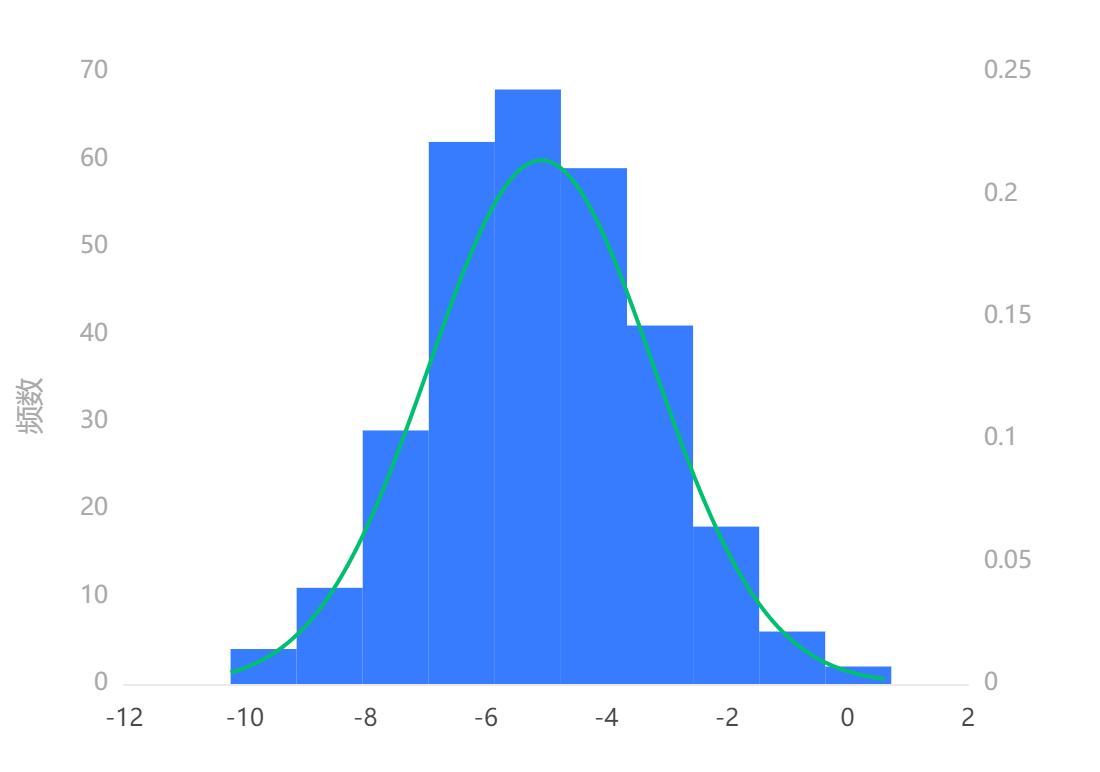

图表说明：
由于上图所示，服药前血压对服药后血压的差值数据基本完美呈现钟形（中间高，两端低），且其峰度（0.007）绝对值小于 10 并且偏度（0.109）绝对值小于 3。
故，虽然检验未通过，还是认为其具有正态性，进行配对样本 T 检验。
​

输出结果 3：配对样本 T 检验结果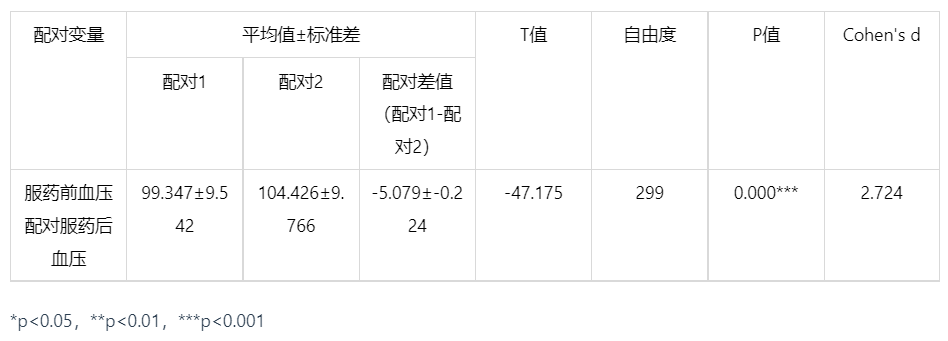

图表说明：配对样本 T 检验的结果显示，基于服药前血压配对服药后血压的差值，显著性 P 值为 0，水平上呈现显著性，拒绝原假设。因此病人注射某药剂前后血压可认为不一致。
而且配对差值为：-5 和差异幅度 Cohen's d 值为：2.724，都可认为差异幅度非常大。

# 7、注意事项

• 配对样本 t 检验的范围是同一组对象，例如一个班级中的女生第一次月考和第二次月考的成绩是否有差异。
• 配对样本 t 检验的使用条件为具有正态性，不具有正态性的数据应该采用非参数检验，如 Wilcoxon 符号秩检验、Nemenyi 检验。
• 各差异性分析模型的使用场景如下总结：

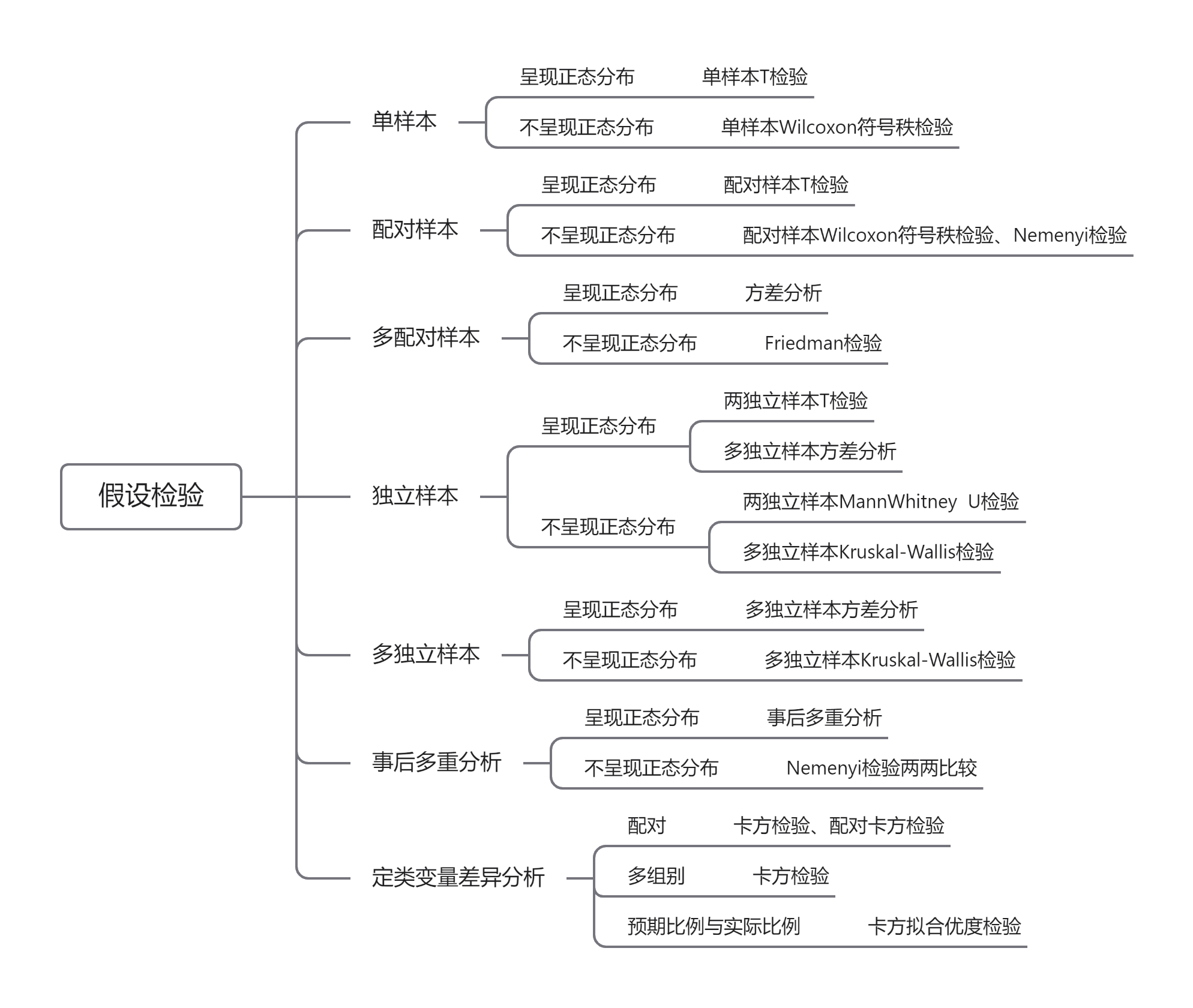
# 8、模型理论

配对样本 t 检验可视为单样本 t 检验的扩展，不过检验的对象由一群来自常态分配独立样本更改为二群配对样本之观测值之差。步骤基本如下：
step1 假设：
零假设：两配对样本的差值 d 均值为 0
备选假设：两配对样本的差值 d 均值不为 0
step2：抽样分布类型
两配对样本的差值 d 近似正态分布，故符合 t 分布条件。
step3：检验方向
备选假设是两配对样本的差值 d 有差别，不管大于还是小于，所以肯定是使用双尾检验。
step4：求解 T 值
基于当前零假设和当前样本，计算 t 值，通过 t 值及比该数值更极端的值出现的概率来代表抽到目前这个样本及更极端的样本的概率。

​step5：计算样本量、自由度求解 p 值
若二配对样本 x1i 与 x2i 之差为 di=x1i−x2i 独立，且来自常态分配，则 di 之母体期望值 μ 是否为 μ0 可利用以下统计量：

其中为配对样本差值之平均数， 为配对样本差值之标准偏差，n为配对样本数。该统计量t在零假说：μ=μ0为真的条件下服从自由度为n−1的t分布。

step6：求解均值置信区间
置信区间下限= 两个平均值差值 - t 值*标准误差
置信区间上限 = 两个平均值差值+ t 值*标准误差
​

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]Fisher Box, Joan. Guinness, Gosset, Fisher, and Small Samples. Statistical Science. 1987, 2 (1): 45–52.