摘要T检验

操作视频

SPSSPRO教程-摘要T检验

# 1、作用

一般进行T检验需要原始数据进行分析，但有时没有原始数据，如数据缺失或者验证论文时。此时只有样本量，平均值，标准差这样的汇总数据，可以使用摘要数据T检验分析差异是否显著。

# 2、输入输出描述

输入：摘要数据(样本量、均值、标准差)以及对应的置信度级别。
输出：单样本T检验或者独立样本T检验的结果。

# 3、案例示例

案例：验证两组病人的血糖是否存在差异性，但是数据缺失，只有汇总数据。一组病人(34人)的饭后血糖均值为4.63，标准差为0.8。另一组(40人)的饭后血糖均值为4.89，标准差为0.62使用摘要数据T检验分析差异是否显著。

# 4、案例数据

摘要T检验案例数据

# 5、案例操作

step1：选择【摘要T检验】；
step2：选择分析类型【单样本T检验OR独立样本T检验】；
step3：输入对应摘要数据(样本量、均值、标准差)，其中两组变量的变量名可以自定义；
step4：选择置信度级别；
step5：点击【开始分析】，完成全部操作；

# 6、输出结果分析

输出结果1：

图表说明：
上表展示了方差齐性的结果，包括标准差、F检验结果、显著性P值。
1. 分析每个分析项的P值是否显著(P<0.05)。
2. 若呈显著性，拒绝原假设（原假设：满足方差齐性），则说明数据波动不一致，即说明方差不齐；反之则说明数据波动一致，说明数据满足方差齐性。
智能分析：
方差齐性检验的结果显示，显著性P值为0.061*，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性。
分析：
用于判断进行T检验的前提条件（满足独立、方差齐、正态性），本次分析通过了方差齐性检验，完成方差齐的条件。

输出结果2：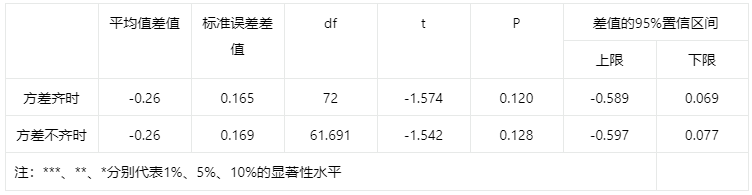

图表说明：
上表展示了独立样本T检验的结果，包括自由度T检验结果，显著性P值、差值的置信区间。
1. 分析每个分析项的P值是否显著(P<0.05)。
2.根据方差齐性检验的结果分析对应行的结果。
3. 若呈显著性，拒绝原假设，说明两组数据之间存在显著性差异，反之则表明数据不呈现差异性。
智能分析：
摘要数据独立样本T检验的结果显示显著性P值为0.128，水平上不呈现显著性，不能拒绝原假设，说明两组样本之间不存在显著差异。
分析：
根据前面的方差齐性结果，选择对应的T检验结果，方差不齐的情况下，给出近似t检验结果供选择。

# 7、注意事项

T检验的前提条件（满足独立、方差齐、正态性），方差齐部分SPSSPRO为您判断，其余两个需要根据数据来源自行判断。

# 8、模型理论

# 单样本T检验：

单样本t检验是检验一个样本平均数与一个已知的总体平均数的差异是否显著。步骤基本如下：
step1假设：
零假设：某个需要检验的值A是不是跟预想中一致，即A平均值等于需要检验的值。
备选假设：A平均值不等于需要检验的值。
step2：抽样分布类型
样本数据集近似正态分布，故符合t分布条件。
step3：检验方向
备选假设是A与检验值不一致，不管大于还是小于，所以肯定是使用双尾检验。
step4：求解T值
基于当前零假设和当前样本，计算t值，通过t值及比该数值更极端的值出现的概率来代表抽到目前这个样本及更极端的样本的概率。
step5：计算样本量、自由度求解p值
单样本t检验统计量为： $t = \frac{\overset{―}{X} - μ}{\frac{σ_{X}}{\sqrt{n}}}$
其中 $i = 1. . . n, \bar{x} = \frac{\sum_{i = 1}^{n} x_{i}}{n}$ 为样本平均数 $s = \sqrt{\frac{\sum_{i = 1}^{n} (x_{i} - \overset{―}{x})^{2}}{n}}$ 为样本标准偏差，n为样本数。
该统计量t在零假说：μ= $μ_{0}$ 为真的条件下服从自由度为n的t分布。
step6：求解均值置信区间
置信区间下限= 两个平均值差值 - t值标准误差
置信区间上限 = 两个平均值差值+ t值标准误差

# 独立样本T检验：

独立样本 t 检验是比较两组数据之间的差异，有无统计学意义，其前提是，两组数据来自正态分布的群体，数据的方差齐，满足独立性。独立样本 t 检验（各实验处理组之间毫无相关存在，即为独立样本），该检验用于检验两组非相关样本被试所获得的数据的差异性。其步骤如下：
step1 假设：
零假设：独立样本 A 和独立样本 B 无差别，即 A 平均值=B 平均值。
备选假设：A 和 B 有差别，也就是 A 平均值不等于 B 平均值。
step2：抽样分布类型
独立样本 A 和独立样本 B 近似正态分布，故符合 t 分布条件。
step3：检验方向
备选假设是 A 和 B 有差别，不管大于还是小于，所以肯定是使用双尾检验。
step4：求解 T 值
基于当前零假设和当前样本，计算 t 值，通过 t 值及比该数值更极端的值出现的概率来代表抽到目前这个样本及更极端的样本的概率。

step5：计算样本量、自由度求解 p 值
独立样本 t 检验使用以下统计量：

$S_{1}^{2}$ 和 $S_{2}^{2}$ 为两样本方差； $n_{1}$ 和 $n_{2}$ 为两样本容量。
step6：求解均值置信区间
置信区间下限= 两个平均值差值 - t 值*标准误差
置信区间上限 = 两个平均值差值+ t 值*标准误差

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2 ]Fisher Box, Joan. Guinness, Gosset, Fisher, and Small Samples. Statistical Science. 1987, 2 (1): 45–52.

建议反馈