梯度提升树(GBDT)分类

操作视频

# 1、作用

GBDT 模型是一个加法模型，它串行地训练一组 CART 回归树，最终对所有回归树的预测结果加和，由此得到一个强学习器，每一颗新树都拟合当前损失函数的负梯度方向。最后输出这一组回归树的加和，套用 sigmod 或者 softmax 函数获得二分类或者多分类结果。

# 2、输入输出描述

输入：自变量 X 为 1 个或 1 个以上的定类或定量变量，因变量 Y 为一个定类变量。
输出：模型的分类结果和模型分类的评价效果。

# 3、案例示例

根据红酒的颜色强度，脯氨酸，类黄酮等变量，生成一个能够区分琴酒，雪莉，贝尔摩德三种品种的红酒的梯度提升树。

# 4、案例数据

梯度提升树分类案例数据

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【梯度提升决策树(GBDT)分类】；
step5：查看对应的数据数据格式，按要求输入【梯度提升决策树(GBDT 分类】数据;
step6：进行参数设置（“更多设置”里的参数在客户端可进行设定）
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：模型参数
图表说明：上表展示了训练该模型的时候，输入的参数以及训练所耗的时间。

输出结果 2：特征重要性

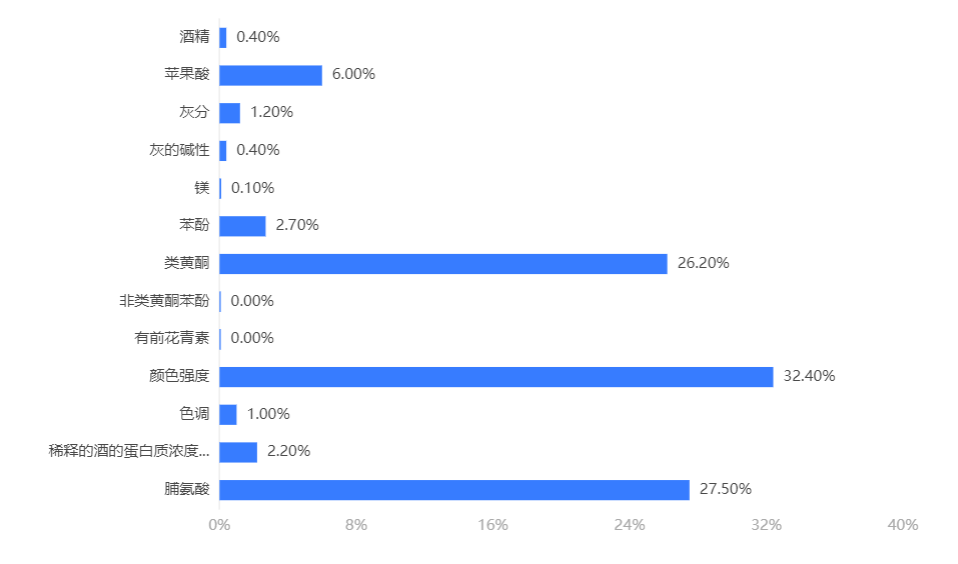
图表说明：上柱形图或表格展示了各特征（自变量）的重要性比例。(附：有时候可以利用特征重要性反推该变量在实际生活中的价值，因为该重要性往往决定分类结果。)
分析：gbdt 模型中决定分类结果的重要因素是颜色强度、脯氨酸、类黄酮和苹果酸。

输出结果 3：混淆矩阵热力图

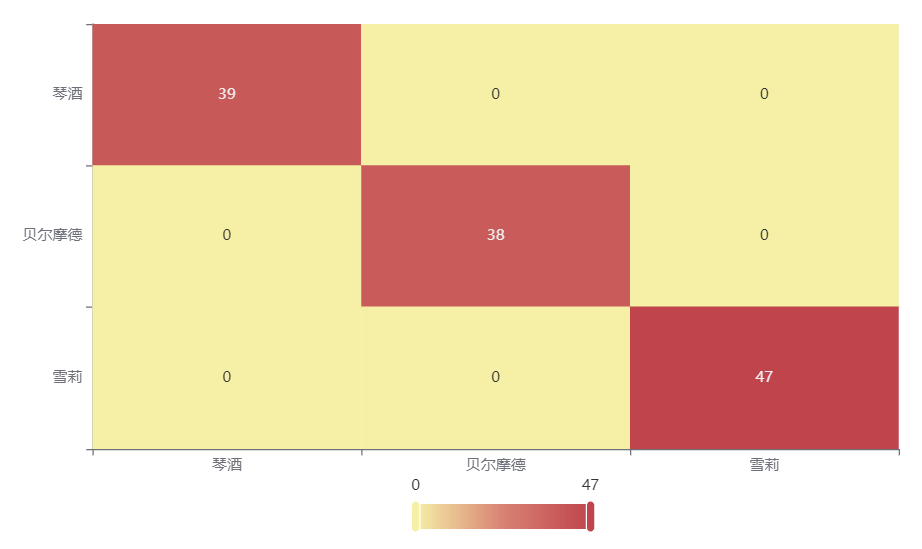
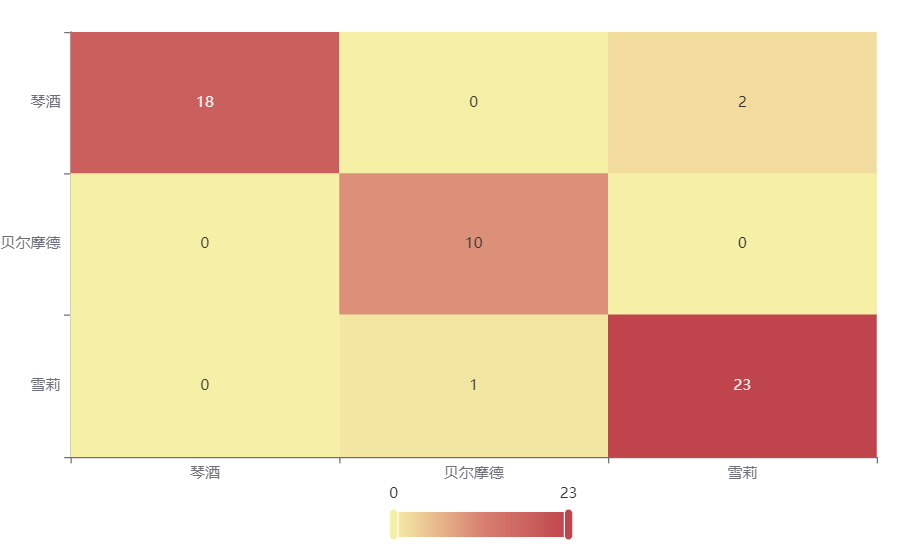
图表说明：上表以热力图的形式展示了混淆矩阵，可以通过右上角切换在测试数据集和训练数据集中的情况。
分析：
上图是训练集的分类结果，所有样本分类正确，说明分类效果极好。
下图是测试集的分类结果，绝大部分样本分类正确，只有 3 个被分错的样本，说明训练集训练出来的模型结果是有效实用的。

输出结果 4：模型评估结果

图表说明：上表中展示了训练集和测试集的分类评价指标，通过量化指标来衡量 gbdt 对训练、测试数据的分类效果。
● 准确率：预测正确样本占总样本的比例，准确率越大越好。
● 召回率：实际为正样本的结果中，预测为正样本的比例，召回率越大越好。
● 精确率：预测出来为正样本的结果中，实际为正样本的比例，精确率越大越好。
● F1：精确率和召回率的调和平均，精确率和召回率是互相影响的，虽然两者都高是一种期望的理想情况，然而实际中常常是精确率高、召回率就低，或者召回率低、但精确率高。若需要兼顾两者，那么就可以用 F1 指标。
分析：
训练集的各分类评价指标都大于 0.9，说明模型在训练集的分类效果极好，模型具有实用性。
测试集的各分类评价指标都大于 0.9，说明模型在测试集的分类效果极好，模型具有实用性。
输出结果 5：测试数据预测评估结果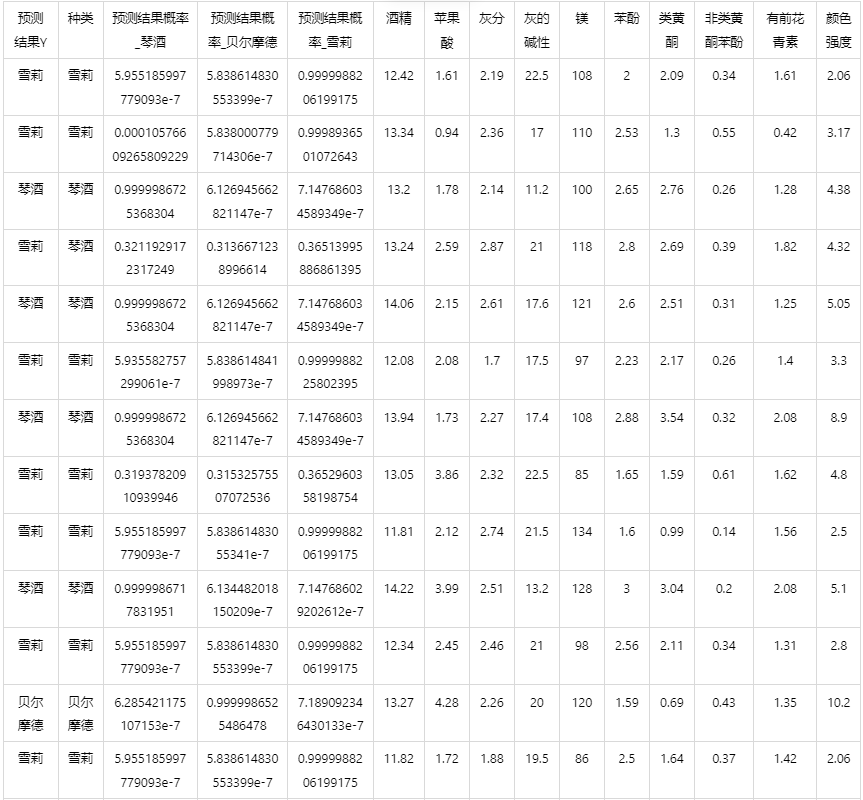

图表说明：上表格为预览结果，只显示部分数据，全部数据请点击下载按钮导出。
上表展示了 gbdt 模型对测试数据的分类结果，第一列是预测结果，第二列是因变量真实值，第三、四、五列分别是对所属每一个分类水平概率的预测结果，最终分类预测结果值是拥有最大预测概率的分类组别。

输出结果 6：模型预测与应用（此功能只在客户端支持使用）
注：当无法进行预测功能时，可检查数据集中是否存在定类变量或者缺失值：
● 当存在定类变量时，请在用于训练模型的数据集和用于预测的数据集中将变量编码，再进行操作。
（SPSSPRO：数据处理->数据编码->将定类变量编码为定量）
● 当用于预测数据的数据集中存在缺失值时，请删去缺失值再进行操作。

情况 1：在上面模型评估后，模型分类结果较好，具有实用性，这时我们将该模型进行应用。点击【模型预测】上传文件可以直接得到预测结果。

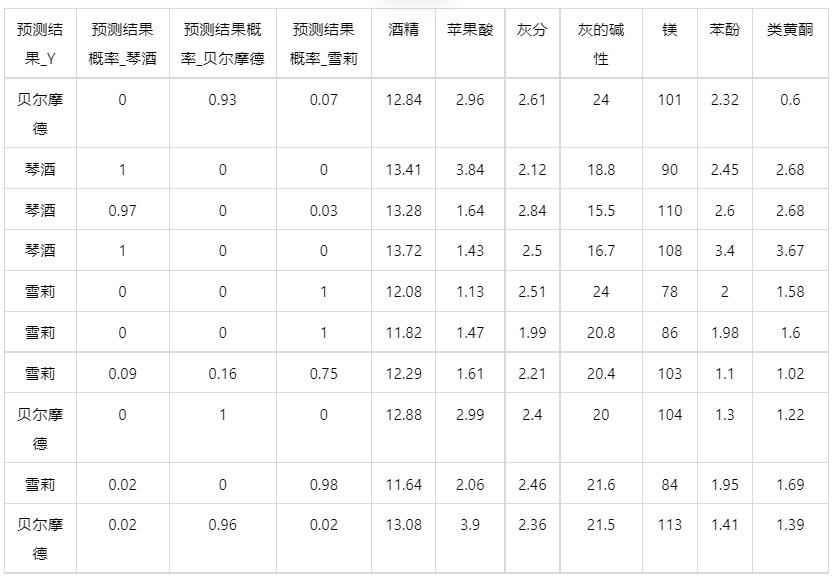
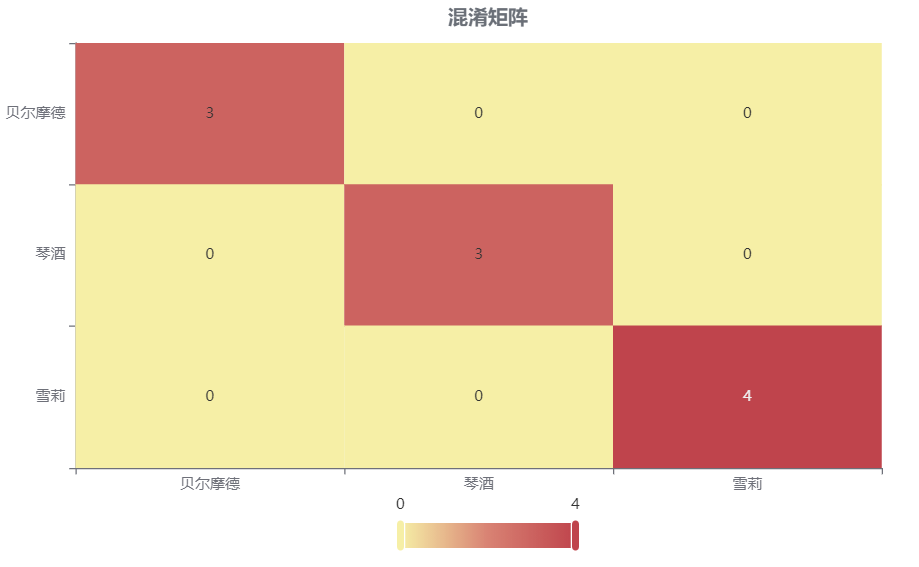
情况 2：若是上传的数据包括因变量真实值，不仅仅可以得到预测结果，还可以得到当前数据分类混淆矩阵和分类评价效果。

# 7、注意事项

由于 GBDT 具有随机性，每次运算的结果不一样。若需要保存本次训练模型，需要使用 SPSSPRO 客户端进行。
GBDT 的参数修改需要使用 SPSSPRO 客户端进行。

# 8、模型理论

GBDT 是以 CART 回归树为基学习器的 Boosting 算法。GBDT 由 Friedman 提出，主要解决一般损失函数的优化问题，其核心思想是通过损失函数的负梯度拟合前一轮基学习器的残差，使每一轮的残差估计逐渐减小，因此每一轮基学习器的输出逐渐逼近真值; 负梯度方向上拟合，可以保证每轮训练都能让损失函数尽可能快减小，加速收敛到局部或全局最优解。

算法实现：
模型输入:训练集 T= {(x1，y1)，(x2，y2)，…，(xN，yN)}，损失函数 L(y，f(x))。

式中:N 表示样本数量,M 表示回归树数量,J 表示回归树叶子节点数量,I(x)表示用于判断集合中元素的指示函数,θ 表示超越参数。

# 9、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]He X , Pan J , Ou J , et al. Practical Lessons from Predicting Clicks on Ads at Facebook[M]. ACM, 2014.

建议反馈