支持向量机(SVR)回归
# 1、作用
支持向量机回归(SVR)用非线性映射将数据映射到高维数据特征空间中,使得在高维数据特征空间中自变量与因变量具有很好的线性回归特征,在该特征空间进行拟合后再返回到原始空间。
# 2、输入输出描述
输入:自变量 X 为 1 个或 1 个以上的定类或定量变量,因变量 Y 为一个定量变量。
输出:模型输出的结果值及模型预测效果。
# 3、案例示例
研究“幸福感”的影响因素,有四个变量可能对幸福感有影响,他们分别是:经济收入、受教育程度、身体健康、情感支持。建立支持向量机回归模型来预测幸福度。
# 4、案例数据
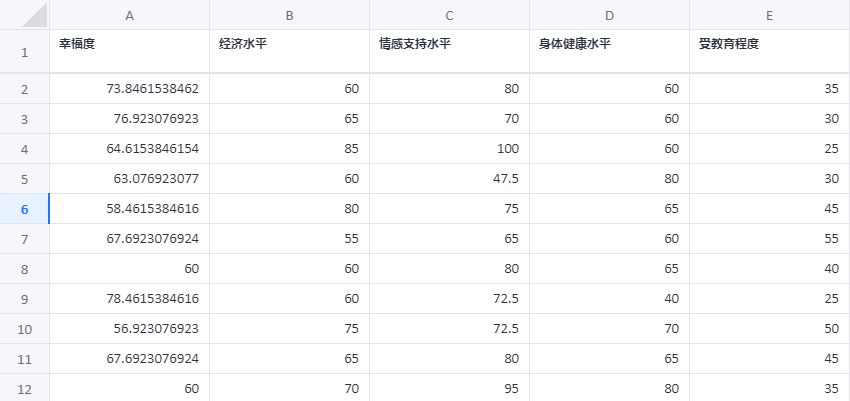
支持向量机回归案例数据
# 5、案例操作
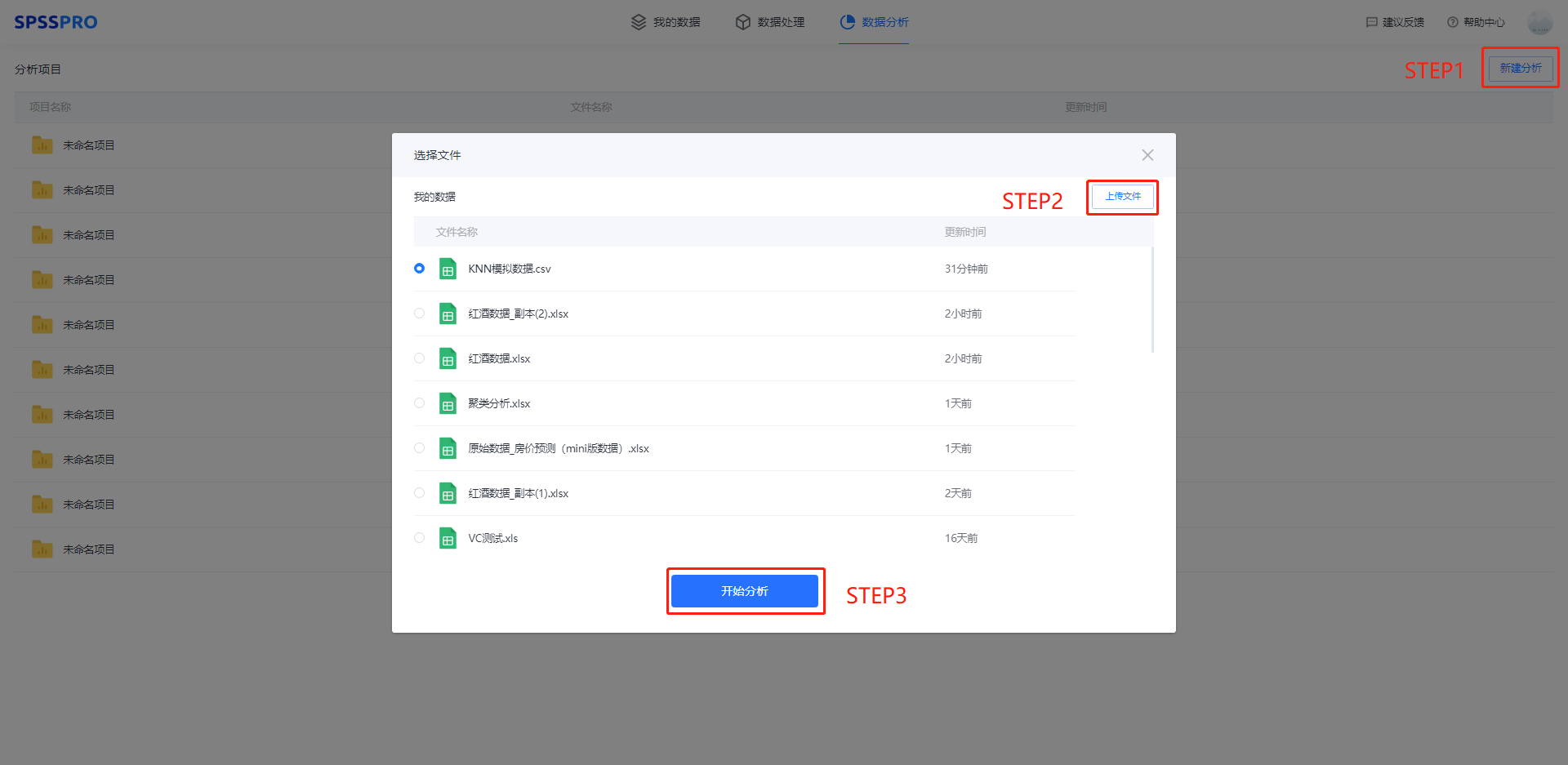
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;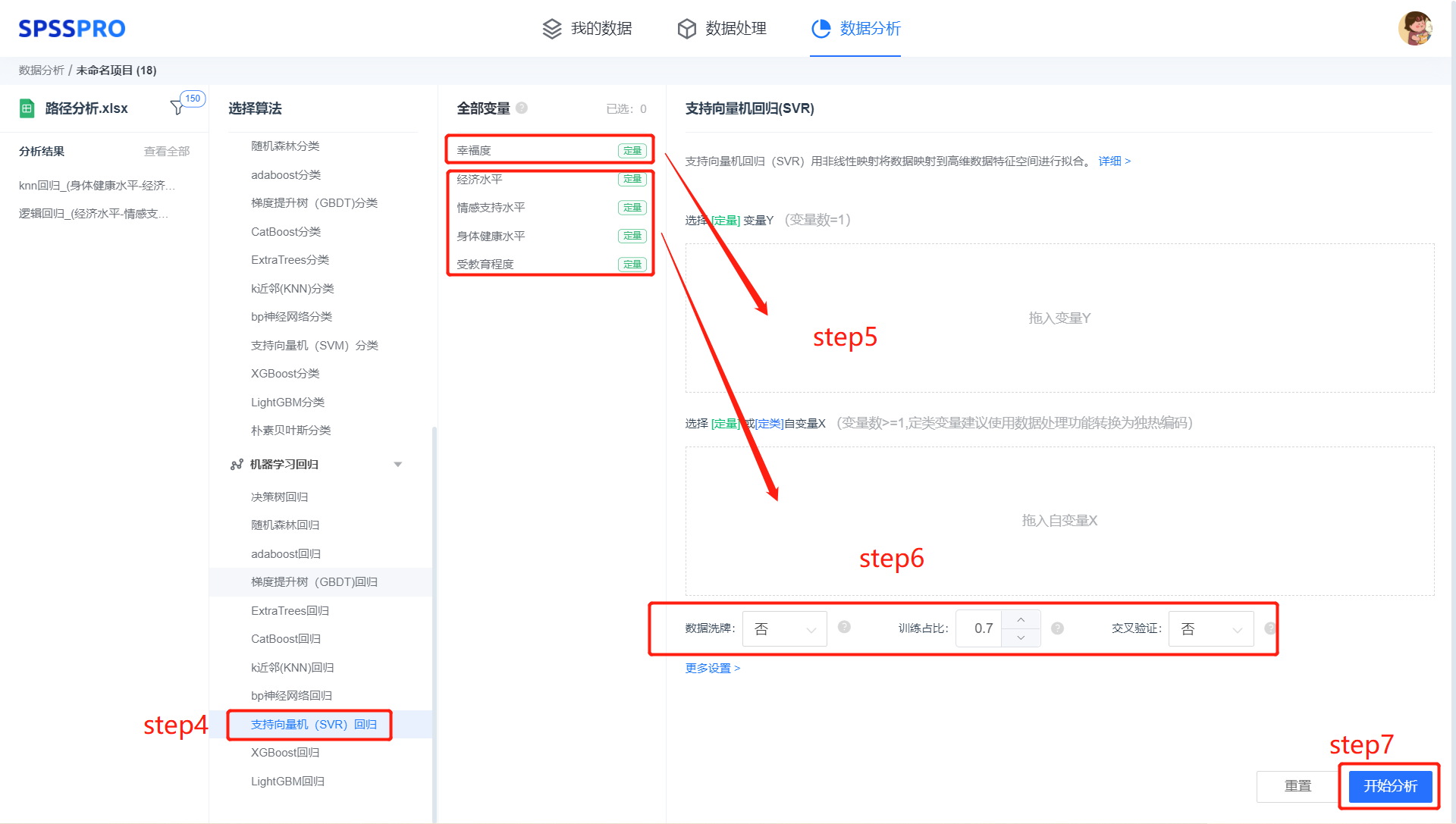
step4:选择【支持向量机(SVR)回归】;
step5:查看对应的数据数据格式,按要求输入【支持向量机(SVR)回归】数据(注:支持向量机(SVR)中定类自变量建议进行编码,定量变量建议标准化);
step6:进行参数设置(“更多设置”里的参数在客户端可进行设定)
step6:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果 1:模型参数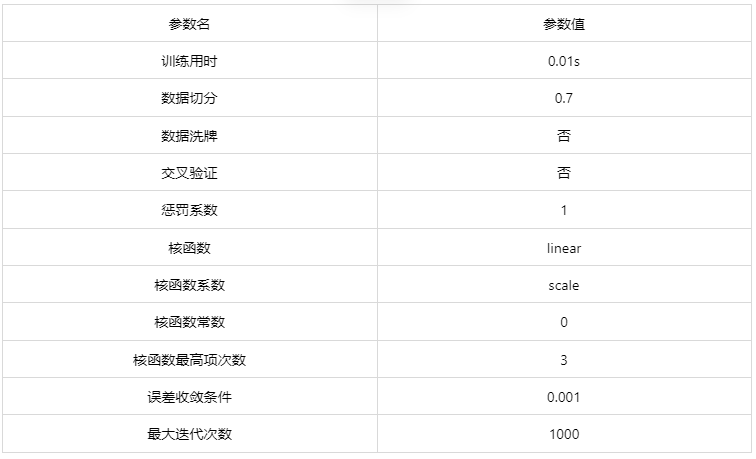
图表说明: 上表展示了训练该模型的时候,输入的参数以及训练所耗的时间。
输出结果 2:模型评估结果
图表说明: 上表中展示了训练集和测试集的预测评价指标,通过量化指标来衡量支持向量机(SVR)的预测效果。
● MSE(均方误差): 预测值与实际值之差平方的期望值。取值越小,模型准确度越高。
● RMSE(均方根误差):为 MSE 的平方根,取值越小,模型准确度越高。
● MAE(平均绝对误差): 绝对误差的平均值,能反映预测值误差的实际情况。取值越小,模型准确度越高。
● MAPE(平均绝对百分比误差): 是 MAE 的变形,它是一个百分比值。取值越小,模型准确度越高。
● R²: 将预测值跟只使用均值的情况下相比,结果越靠近 1 模型准确度越高。
分析:
训练集测试集的各预测评价指标值相差不大,就平均绝对百分比误差来看,误差率仅 10%左右,模型预测一般。
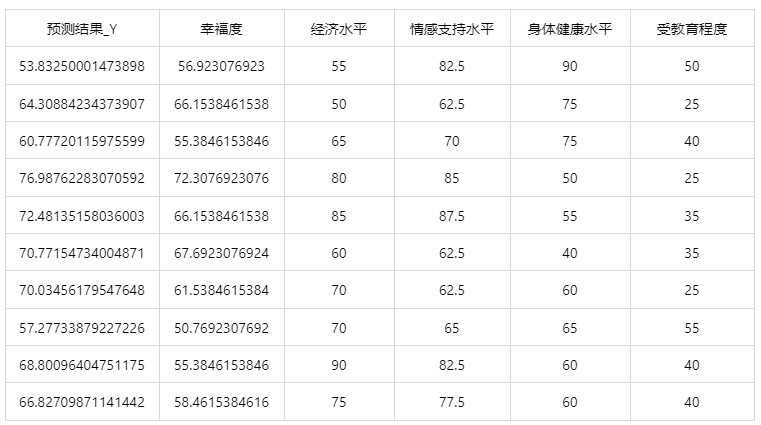
输出结果 3:测试数据预测结果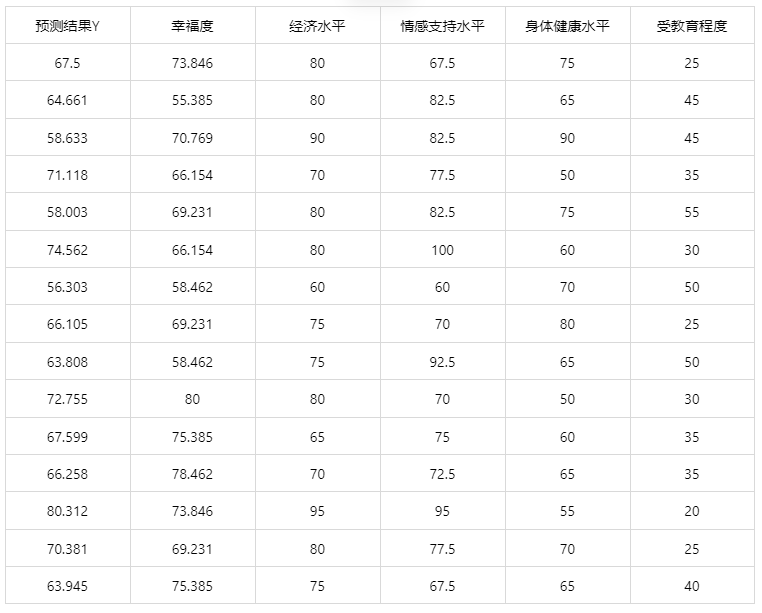
图表说明: 上表格为预览结果,只显示部分数据,全部数据请点击下载按钮导出。
上表展示了支持向量机(SVR)模型对测试数据的预测结果,第一列是预测结果,第二列是因变量真实值,其余列是各自变量的值。
输出结果 4:测试数据预测图 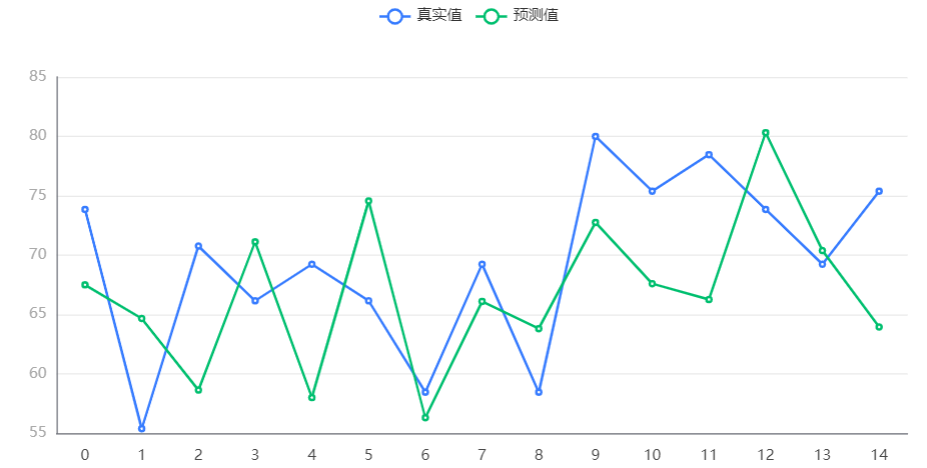
图表说明:上图中展示了支持向量机回归对测试数据的预测情况。
输出结果 5:模型预测与应用(此功能只在客户端支持使用)
注:当无法进行预测功能时,可检查数据集中是否存在定类变量或者缺失值:
● 当存在定类变量时,请在用于训练模型的数据集和用于预测的数据集中将变量编码,再进行操作。
(SPSSPRO:数据处理->数据编码->将定类变量编码为定量)
● 当用于预测数据的数据集中存在缺失值时,请删去缺失值再进行操作。
情况 1:在上面模型评估后,模型分类结果较好,具有实用性,这时我们将该模型进行应用。点击【模型预测】上传文件可以直接得到预测结果。
经上述操作后,得到以下结果: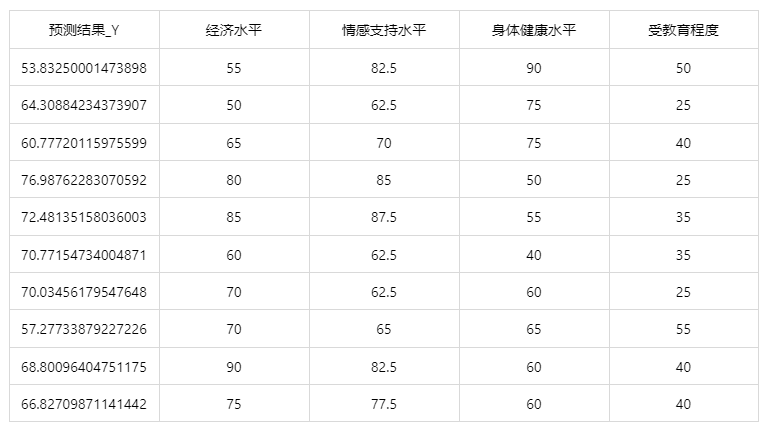
情况 2:若是上传的数据包括因变量真实值,不仅仅可以得到预测结果,还可以得到当前应用数据预测评估效果。
经上述操作后,得到以下结果: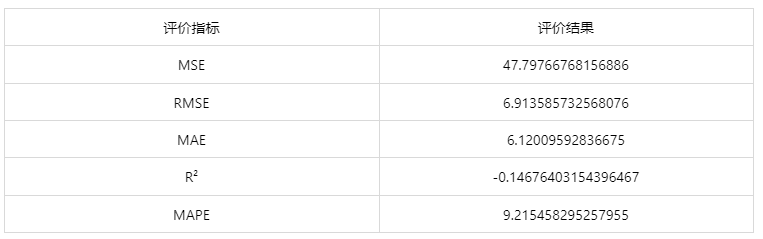
# 7、注意事项
- 由于支持向量机(SVR)具有随机性,每次运算的结果不一样。若需要保存本次训练模型,需要使用 SPSSPRO 客户端进行。
- 支持向量机(SVR)的参数修改需要使用 SPSSPRO 客户端进行。
# 8、模型理论
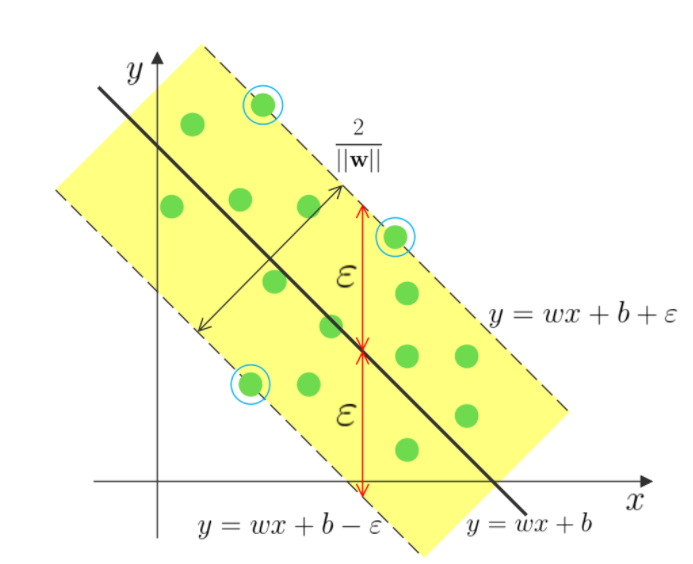
对于一般的回归问题,给定训练样本 D={(x1,y1),(x2,y2),...,(xn,yn)},我们希望学习到一个 f(x)使得其与 y 尽可能的接近,w,b 是待确定的参数。在这个模型中,只有当 f(x)与 y 完全相同时,损失才为零,而支持向量回归假设我们能容忍的 f(x)与 y 之间最多有 ε 的偏差,当且仅当 f(x)与 y 的差别绝对值大于 ε 时,才计算损失,此时相当于以 f(x)为中心,构建一个宽度为 2ε 的间隔带,若训练样本落入此间隔带,则认为是被预测正确的。(间隔带两侧的松弛程度可有所不同)
因此 SVR 问题可转化为(下式左部是正则化项):
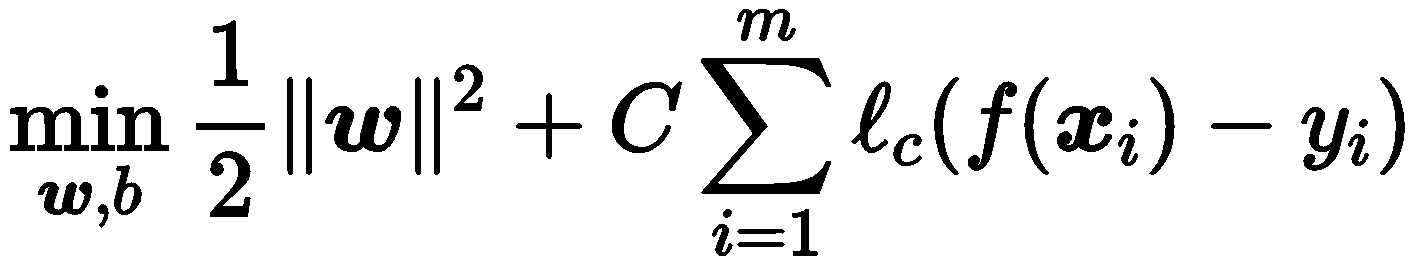
上式左部是正则化项,右部式损失函数:

因此引入了松弛因子,SVR 问题就是:
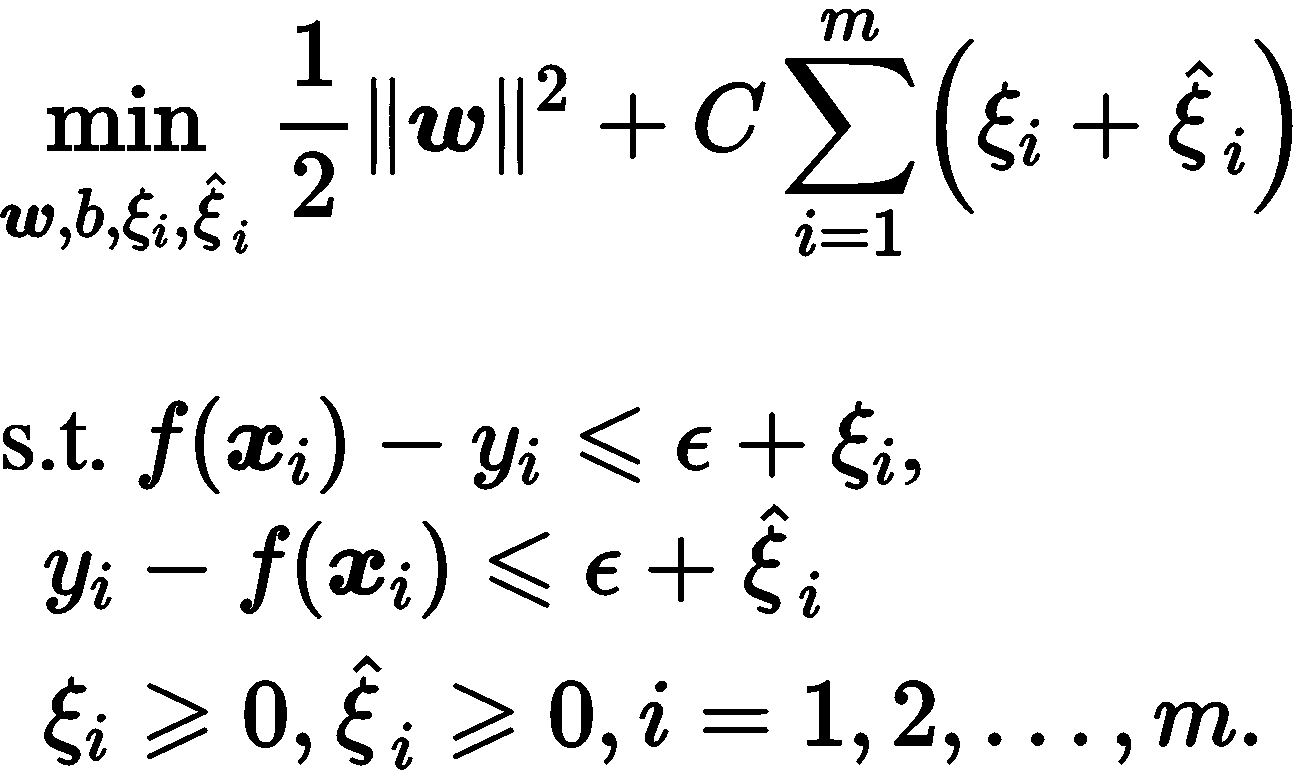
最后引入拉格朗日乘子,可得拉格朗日函数:
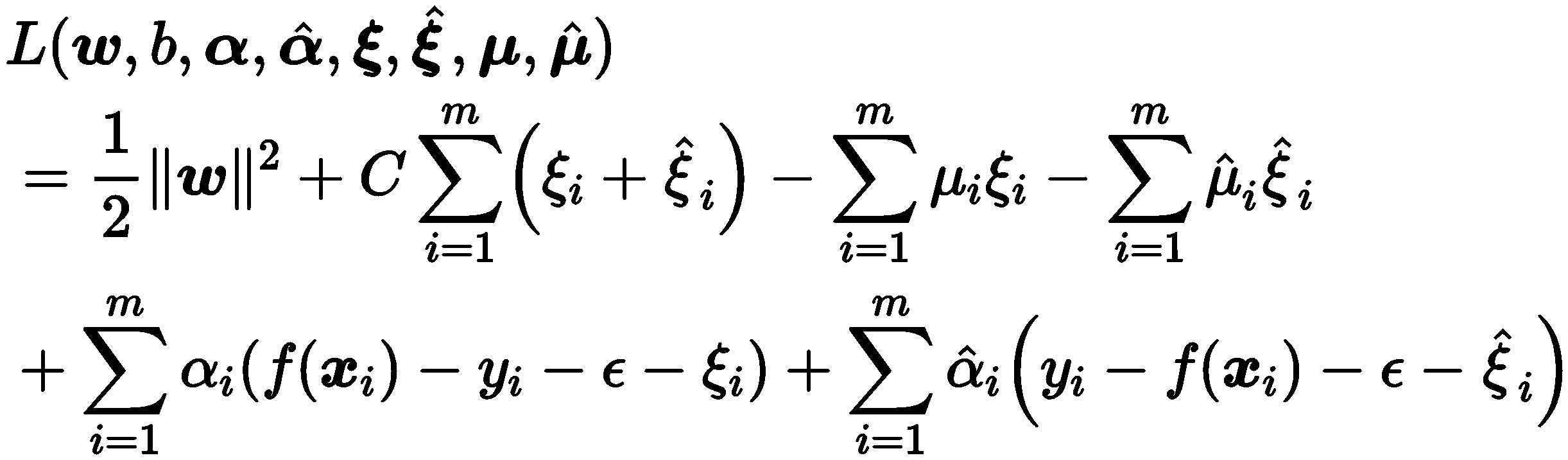
对四个遍历求偏导,令偏导数为零,可得
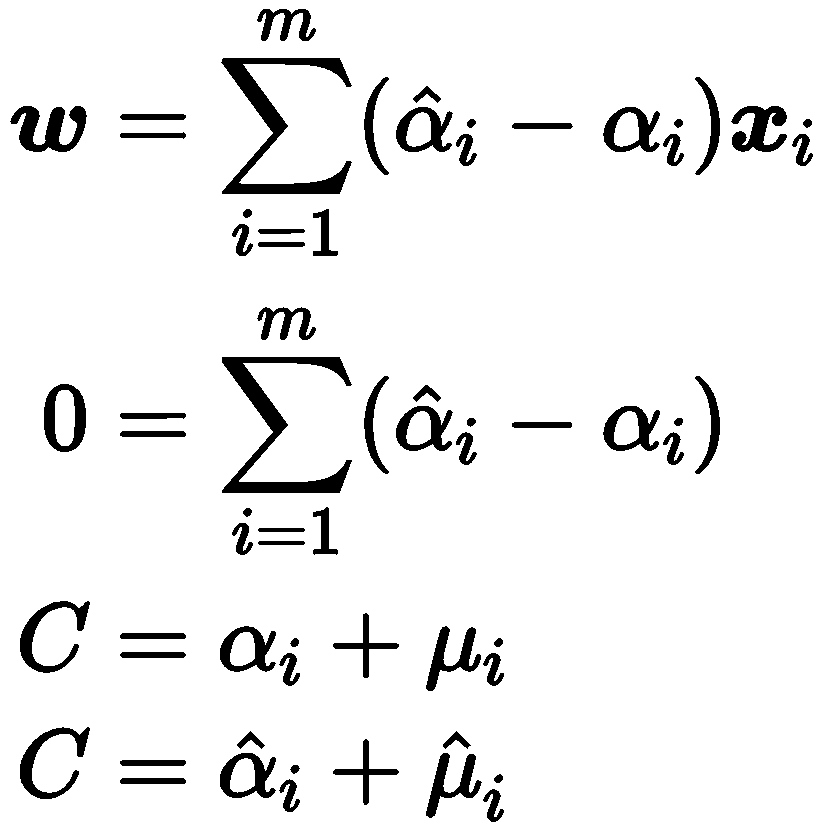
把上边的式子带入,即可求得 SVR 的对偶问题
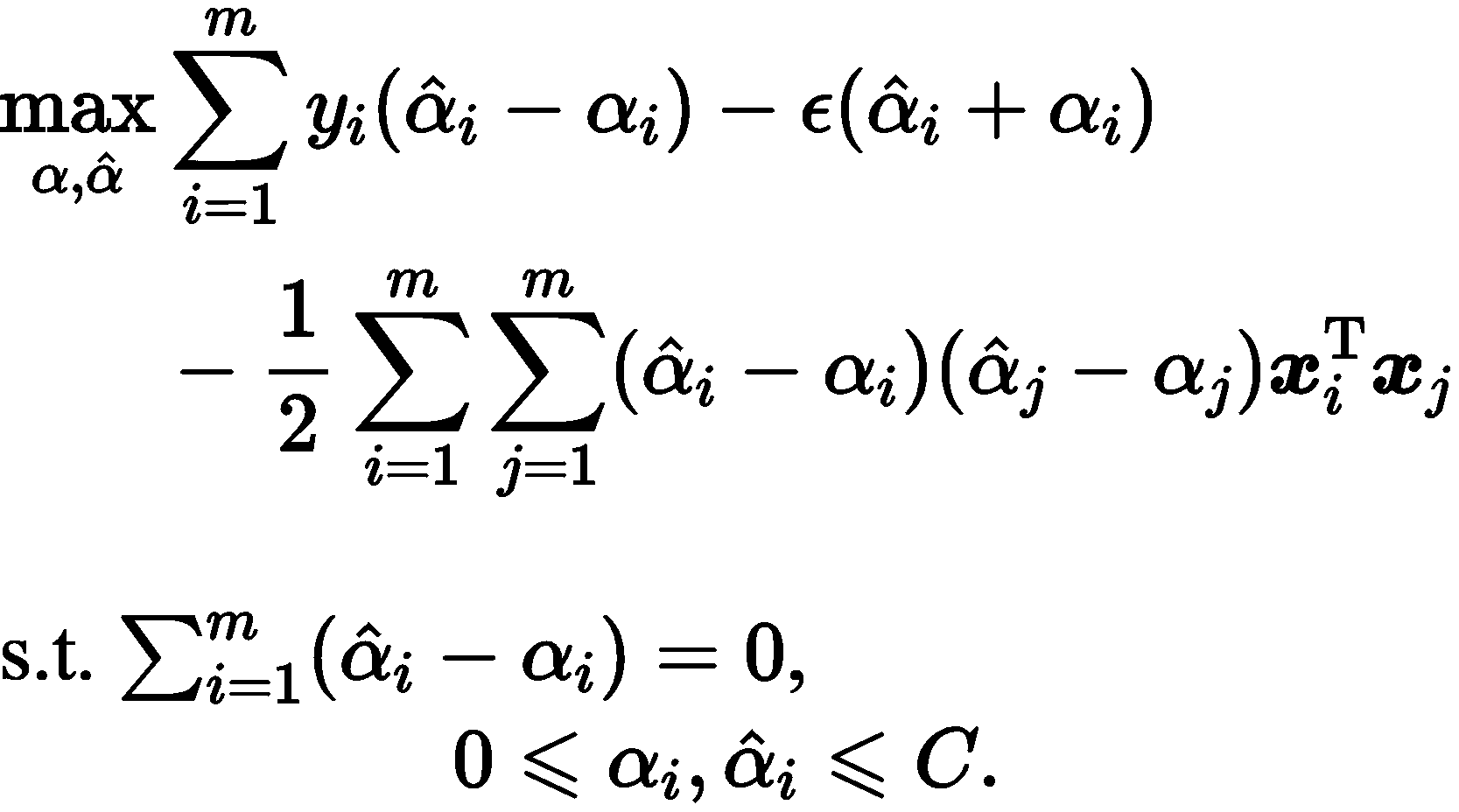
上边的过程需要满足 KKT 条件,即
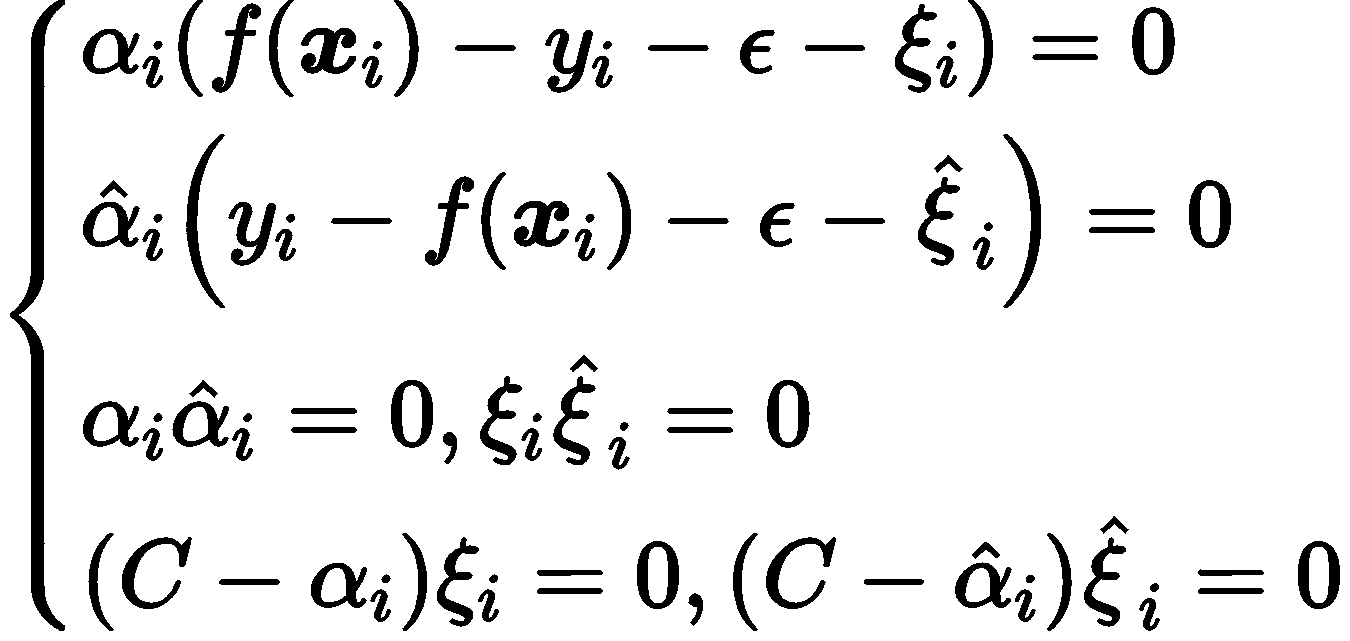
最后,可得 SVR 的解为
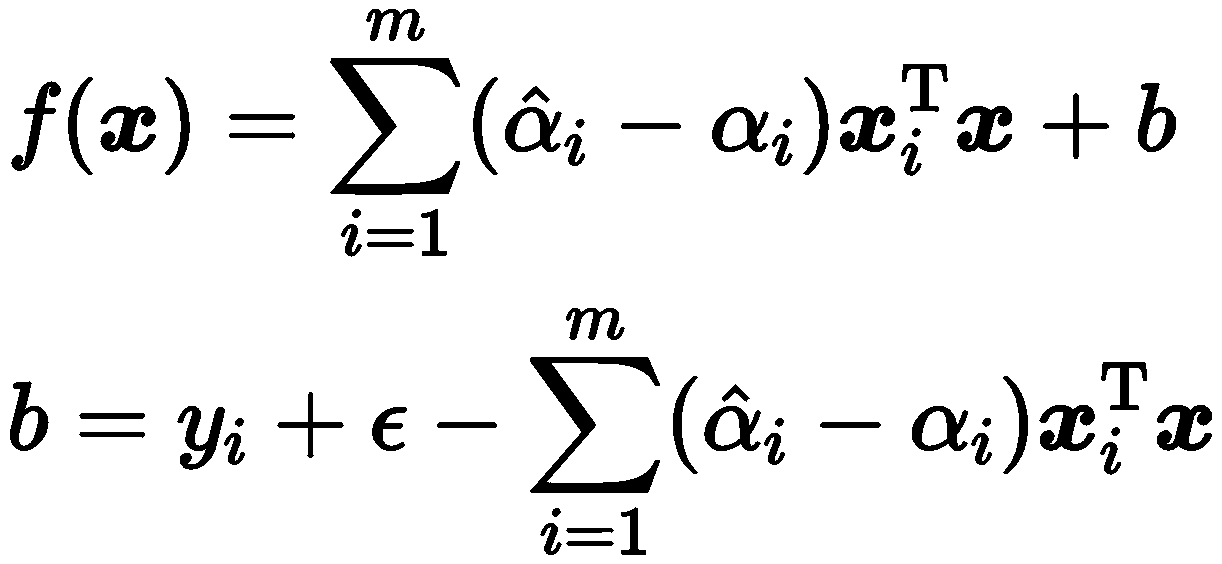
#
9、参考文献
[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]Vapnik, V..Statistical learning theory. 1998 (Vol. 3). .New York, NY:Wiley,1998:Chapter 10-11, pp.401-492
[3] 周志华.机器学习.北京:清华大学出版社,2016:pp.121-139, 298-300
[4]李航.统计学习方法.北京:清华大学出版社,2012:第七章,pp.95-135
