线性回归(梯度下降法)

# 1、作用

线性回归是利用线性回归方程对一个或多个自变量与因变量之间关系进行建模的一种回归分析。

# 2、输入输出描述

输入：自变量 X 为 1 个或 1 个以上的定类或定量变量，因变量 Y 为一个定量变量。
输出：模型输出的分析结果及模型的预测效果。

# 3、案例示例

根据房子的房龄、步行生活圈便利店数量和到地铁站距离，使用线性回归方法预估该房子的单位面积房价。

# 4、案例数据

线性回归案例数据

# 5、案例操作

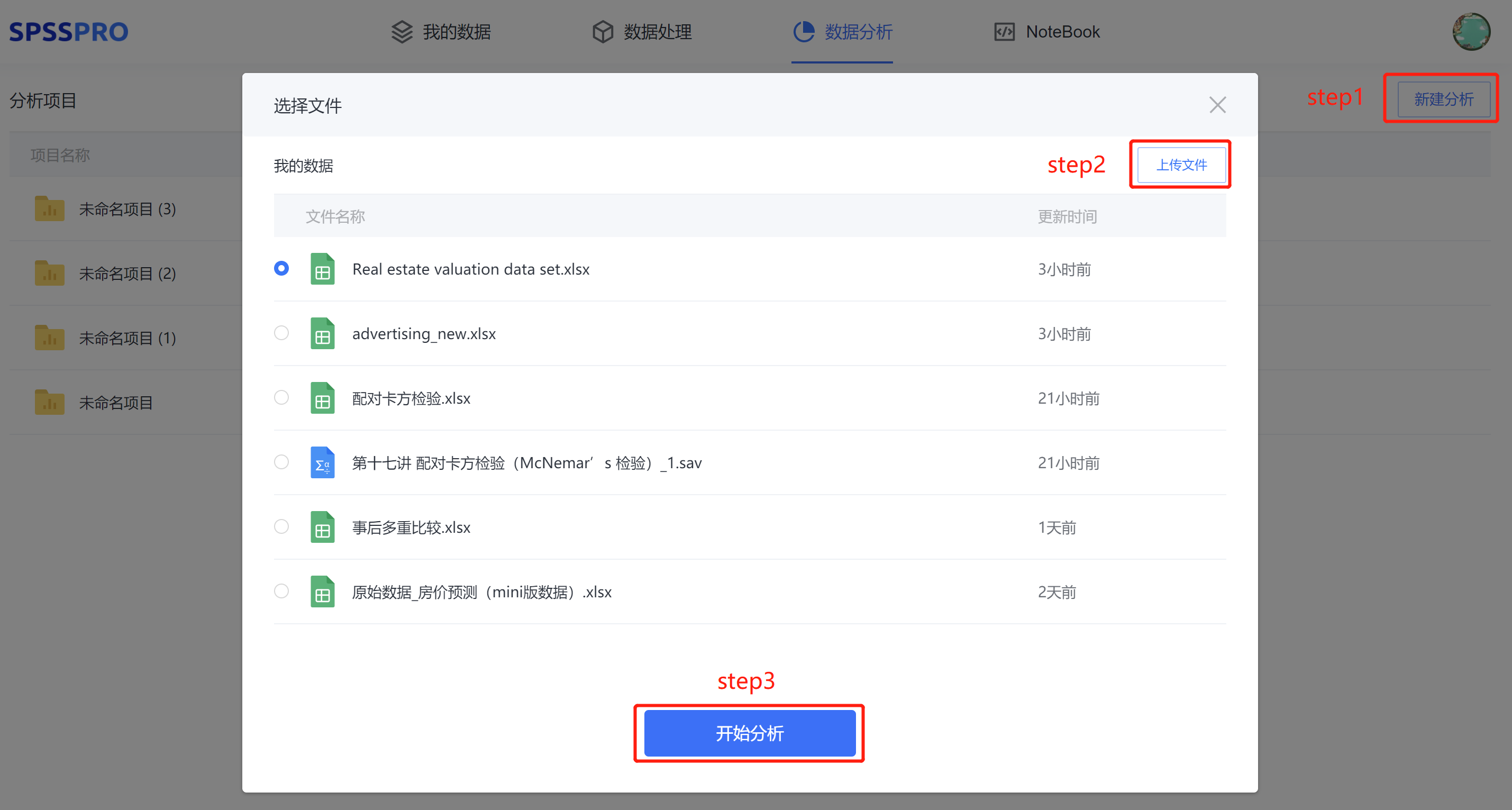
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；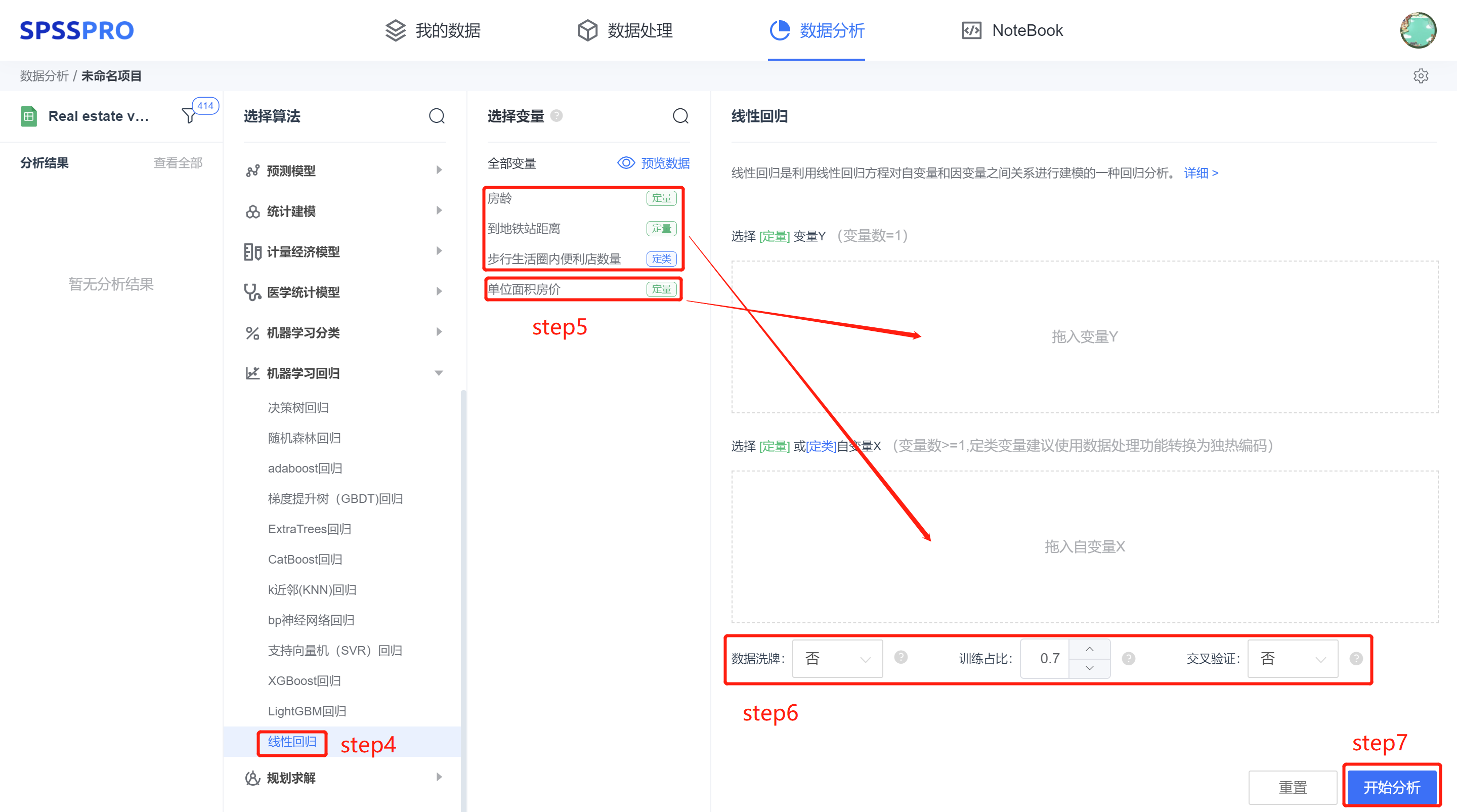

step4：选择【线性回归】；
step5：查看对应的数据数据格式，按要求输入【线性回归】数据;
step6：设置训练方式及参数；
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：特征重要性

图表说明：上表展示了模型各个特征的权重，其中负号代表负向影响，正号代表正向影响。
分析：线性回归模型认为，该案例下生活圈便利店数量是对房价的最重要影响因素，到地铁站距离是对房价影响最小的因素。

输出结果 2：模型评估结果

	MSE	RMSE	MAE	MAPE	R²
训练集	92.052	9.594	6.633	21.322	0.529
测试集	68.596	8.282	6.265	18.239	0.571

图表说明：上表中展示了交叉验证集、训练集和测试集的预测评价指标，通过量化指标来衡量线性回归模型的预测效果。其中，通过交叉验证集的评价指标可以不断调整超参数，以得到可靠稳定的模型。
● MSE（均方误差）：预测值与实际值之差平方的期望值。取值越小，模型准确度越高。
● RMSE（均方根误差）：为 MSE 的平方根，取值越小，模型准确度越高。
● MAE（平均绝对误差）：绝对误差的平均值，能反映预测值误差的实际情况。取值越小，模型准确度越高。
● MAPE（平均绝对百分比误差）：是 MAE 的变形，它是一个百分比值。取值越小，模型准确度越高。
● R²：将预测值跟只使用均值的情况下相比，结果越靠近 1 模型准确度越高。

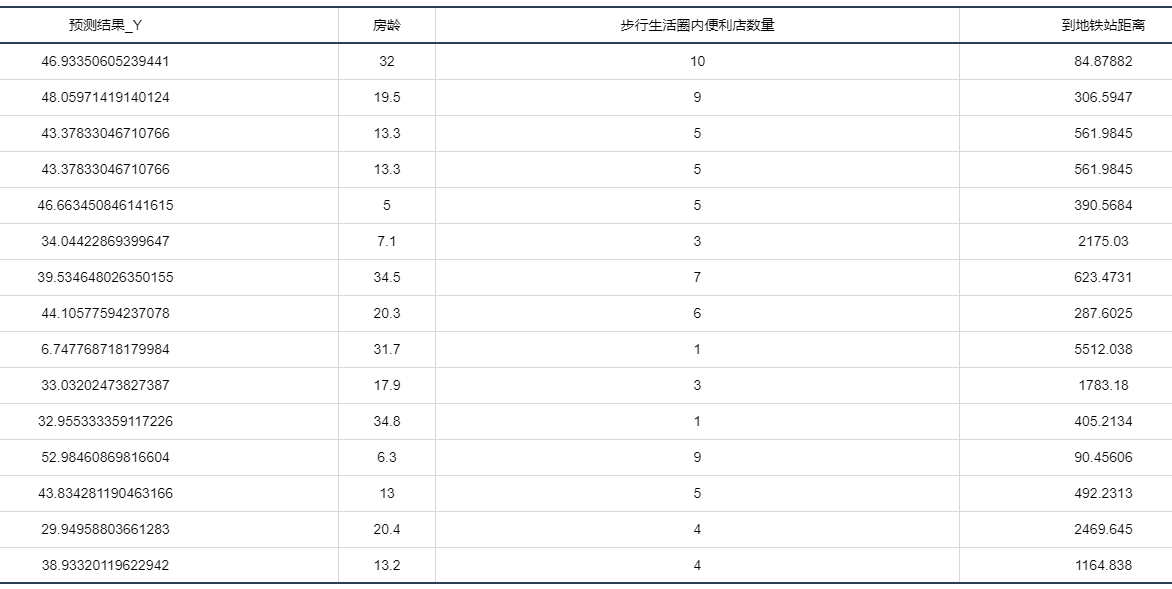
输出结果 3：测试数据预测结果

图表说明：上表格为预览结果，只显示部分数据，全部数据请点击下载按钮导出。上表展示了线性回归模型对测试数据的预测情况。

输出结果 4：测试数据预测图

图表说明：上图中展示了线性回归模型对测试数据的预测情况。

输出结果 5：模型预测与应用（此功能只在客户端支持使用）
注：当无法进行预测功能时，可检查数据集中是否存在定类变量或者缺失值：
● 当存在定类变量时，请在用于训练模型的数据集和用于预测的数据集中将变量编码，再进行操作。
（SPSSPRO：数据处理->数据编码->将定类变量编码为定量）
● 当用于预测数据的数据集中存在缺失值时，请删去缺失值再进行操作。
情况 1：在上面模型评估后，模型预测结果较好，具有实用性，这时我们将该模型进行应用。点击【模型预测】上传文件可以直接得到预测结果。

情况 2：若是上传的数据包括因变量真实值，不仅仅可以得到预测结果，还可以得到评价效果。

评价指标	评价结果
MSE	84.9702039145737
RMSE	9.217928396042883
MAE	6.522120844864839
R²	0.5399289741838798
MAPE	20.391458396898663

图表说明：上表中展示了真实值和预测值的评价指标，通过量化指标来衡量线性回归对上传数据的预测效果。
● MSE（均方误差）：预测值与实际值之差平方的期望值。取值越小，模型准确度越高。
● RMSE（均方根误差）：为 MSE 的平方根，取值越小，模型准确度越高。
● MAE（平均绝对误差）：绝对误差的平均值，能反映预测值误差的实际情况。取值越小，模型准确度越高。
● MAPE（平均绝对百分比误差）：是 MAE 的变形，它是一个百分比值。取值越小，模型准确度越高。
● R²：将预测值跟只使用均值的情况下相比，结果越靠近 1 模型准确度越高。

# 7、注意事项

作简单线性回归分析要有实际意义，不要把毫无关联的两种现象强加在一起作回归分析。
在作线性回归分析前，一定要绘制散点图，观察全部数据点的分布趋势，只有存在线性趋势时，才可以进行线性回归分析。
线性回归方程的适用范围一般以自变量的取值范围为限。
有回归关系不能证明事物间有因果关系。

# 8、模型理论

1. 一元线性回归 一元线性回归是最简单的线性回归模型。比如中学的二元一次方程，我们将 y 作为因变量，x 作为自变量，得到方程：

当给定参数和的时候，画在坐标图内是一条直线。
当我们只用一个 x 来预测 y，就是一元线性回归，也就是找一个直线来拟合数据。比如，我有一组数据画出来的散点图，横坐标代表房屋面积，纵坐标代表总价，线性回归就是要找一条直线，并且让这条直线尽可能地拟合图中的数据点。

我们得到的拟合方程是 y = 1.302x + 11.2，此时当有房屋出售时，我们就可以用该方程预测出大概总价。
数学理论的世界是精确的，譬如我们代入 x=60 就能得到唯一的，=89.427（不是真实观测到的，而是估计值）。但现实世界中的数据就像这个散点图，我们只能尽可能地在杂乱中寻找规律，真实值与估计值之间的存在一定的误差。

2.损失函数 既然是用直线拟合散点，最终得到的直线是 y = 1.302x + 11.2，还是下图中的 y = 1.14x + 10.5 呢？这两条线看起来都可以拟合这些数据，所以我们要找到一个评判标准，用于评价哪条直线才是最合适的。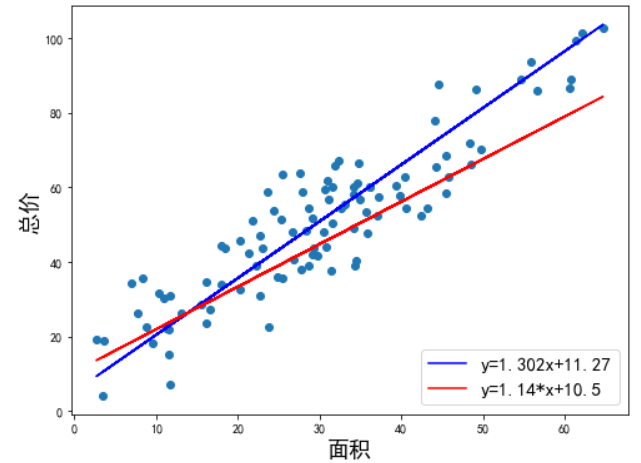

先从残差说起，残差即真实值和预测值间的差值（也可理解为差距），用公式表示是：。

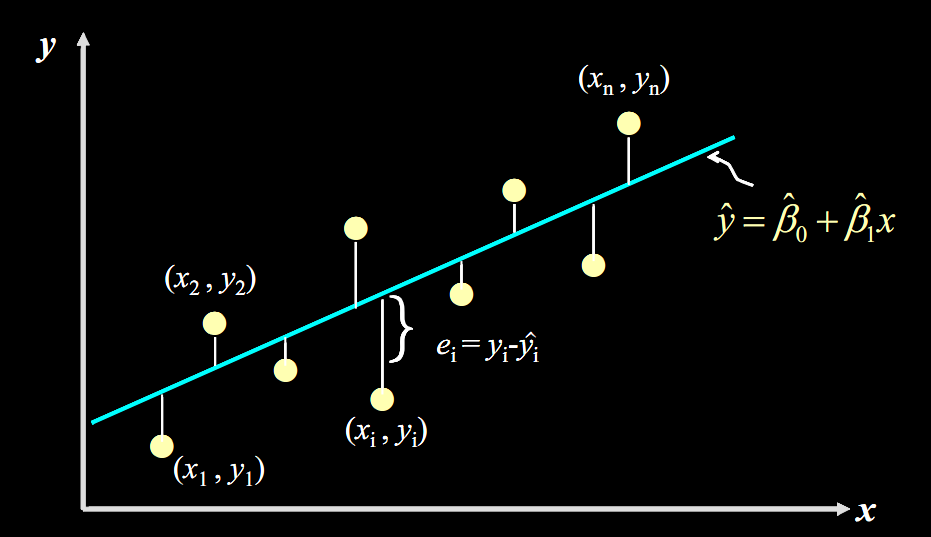
对于某个房屋面积，我们有对应的实际销售总价，和预测出来的销售总价（通过将代入公式计算得到），计算的值，再将其平方（为了消除负号），对于我们数据中的每个点这样计算，再将所有的相加，就能量化出拟合的直线和实际之间的误差。用公式表示就是：

这个公式是残差平方和，即 SSE（Sum of Squares for Error），在机器学习中它是回归问题中最常用的损失函数。**损失函数是衡量回归模型误差的函数，也就是我们要的“直线”的评价标准。**损失函数的值越小，说明直线越能拟合我们的数据。

3.梯度下降法 那么，这个和的具体值该如何计算？
给定一组样本观测值，（i=1,2,…n），要求回归函数尽可能拟合这组值。最小二乘法将问题转化为求损失函数的偏导数，计算损失函数的最小值，通过联立方程组得出和。最小二乘法最后一步要求方程组，当自变量较多时，是非常大的计算量，计算起来很难，因此需要使用一种新的计算方法，就是梯度下降法。
我们将最小二乘法的 Q 改为代价函数：,m 为数据个数，分母上的 2 为了抵消求导后的系数。
此时， $和$ 通过以下式子计算：

，（式中以 := 为赋值符号）。
代价函数的图大致如下：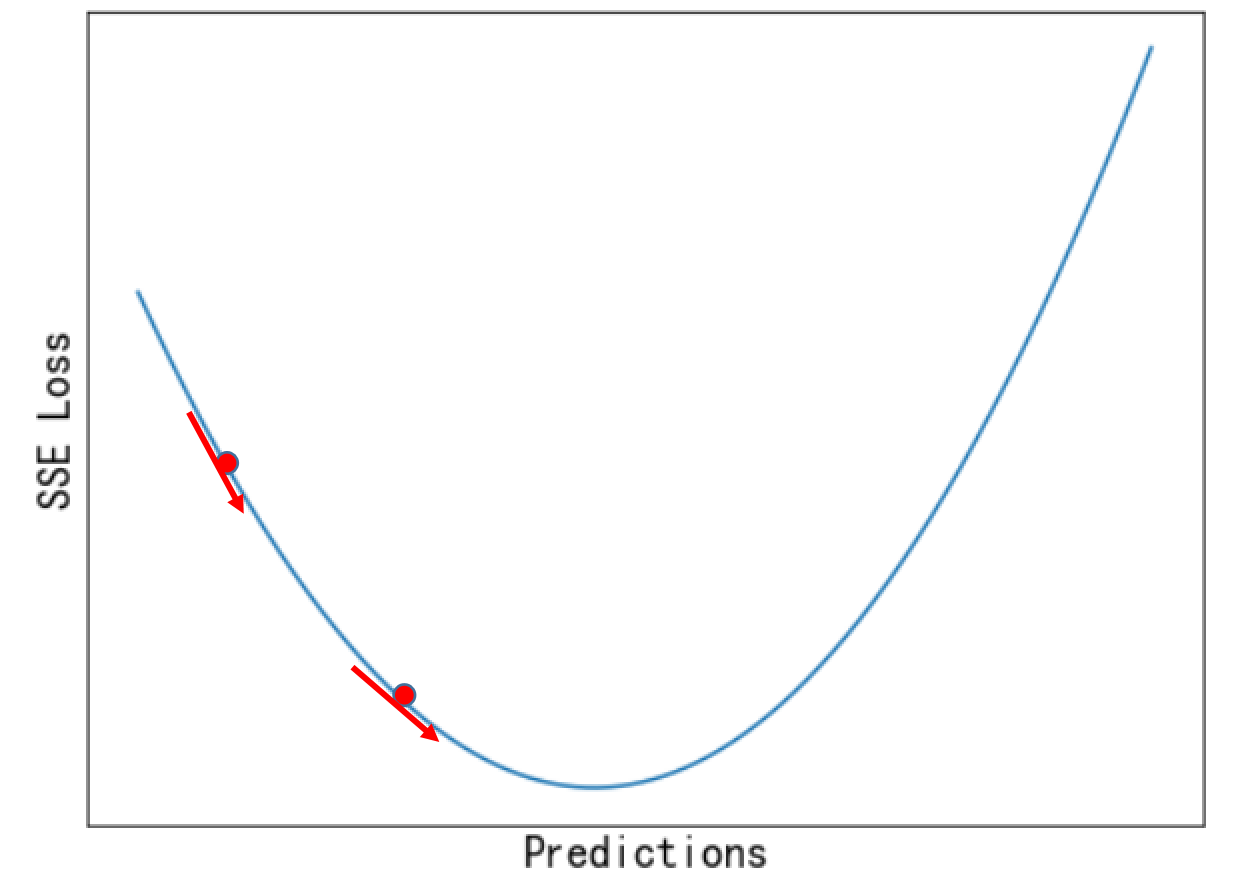

图中的最低点为代价函数最小处，也就是我们需要找到的点，可以将过程想想为一个下山的过程。梯度下降法的思想是一步步寻找最优，通过计算每一点的梯度，决定下一步的移动方向，是一个反复迭代的过程，直到找到满足要求的点。

需要知道的是：

起始位置需要设定，通常设置，也可以随机设置；
每一步走多远，由上式中的学习率决定，越大，走的越快，但并不是越大越好，因为在接近最低点时可能会直接跨过，然后在最低点左右反复徘徊；越小，则走的很慢，因此需要权衡考虑；
另外，梯度下降法需要设定一个条件决定停止迭代的时刻，可以设定一个阈值，通过计算梯度向量的模判断算法是否收敛。

梯度下降法主要包括以下步骤：

给定待优化连续可微代价函数、学习率及初始值；
计算待优化函数梯度；
更新迭代公式，;
计算该处的函数梯度；
计算梯度向量的模判断是否收敛：；
若收敛，算法停止，否则从第 3 步开始继续迭代直至收敛。

4.总结 与最小二乘法相比，梯度下降法在特征较大时，也可以计算，而最小二乘法的时间复杂度会很大；另外，最小二乘法只适用于线性模型；而梯度下降适用性极强，一般只要是凸函数，都可以通过梯度下降法得到全局最优值。常见的梯度下降法包括批量梯度下降算法、随机梯度下降法和小批量梯度下降法等。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Montgomery, D. C. , E. A. Peck , and G. G. Vining . Introduction to linear regression analysis. Wiley, 1982.

建议反馈