adaboost回归

# 1、作用

adaboost给予误差率低的学习器一个高的权重，给予误差率高的学习器一个低的权重，结合弱学习器和对应的权重，生成强学习器。回归问题与分类问题算法的不同点在于误差率计算的方式不同，分类问题一般都采用0/1损失函数，而回归问题一般都是平方损失函数或者是线性损失函数。

# 2、输入输出描述

输入：自变量X为1个或1个以上的定类或定量变量，因变量Y为一个定量变量。
输出：模型输出的预测结果及模型的分类效果。

# 3、案例示例

根据房子的户型、电梯、面积、房龄、装修程度、容积率和绿化率，使用adaboost回归方法预估该房子的房价。

# 4、案例数据

adaboost回归案例数据

# 5、案例操作

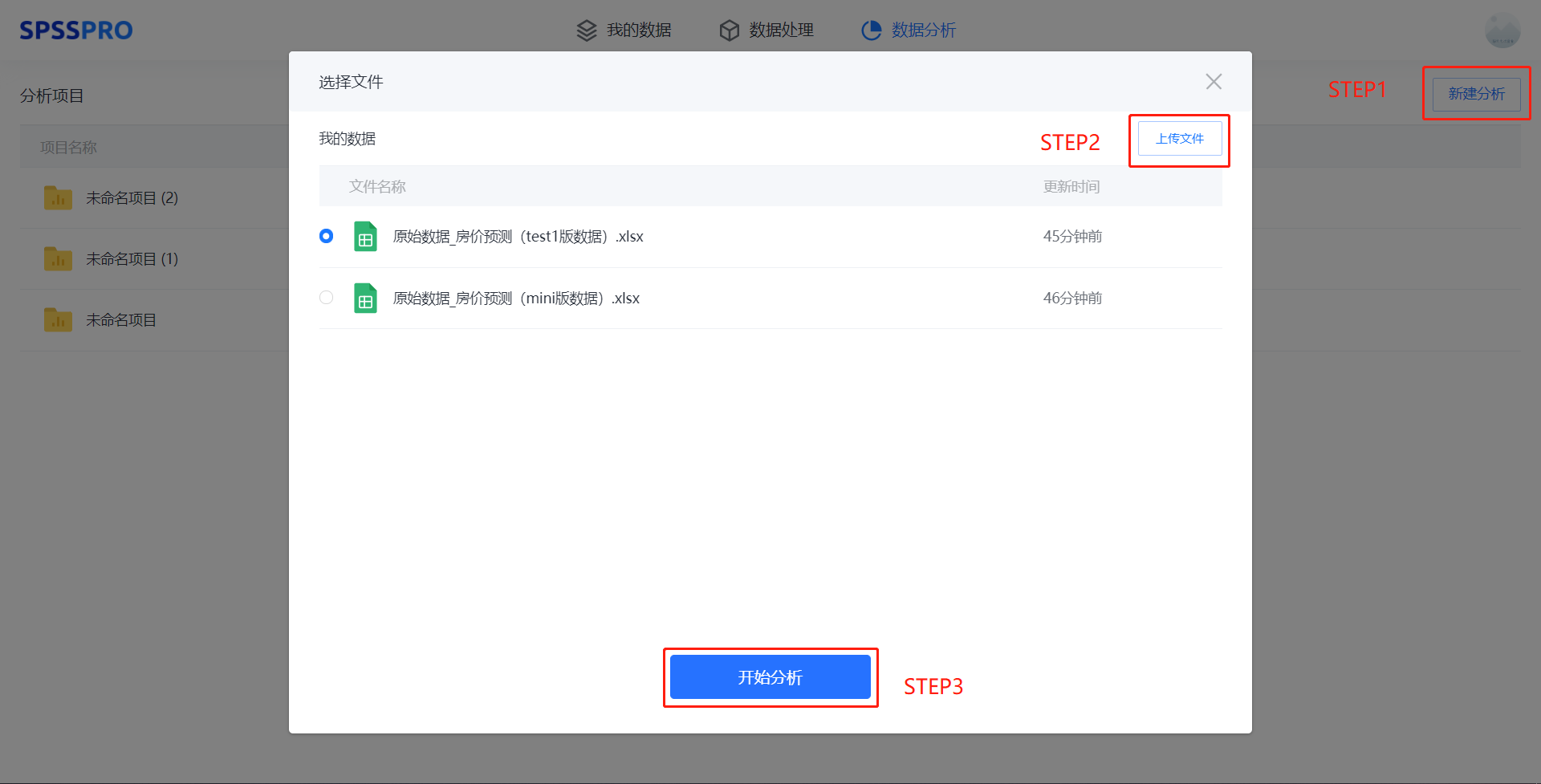
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；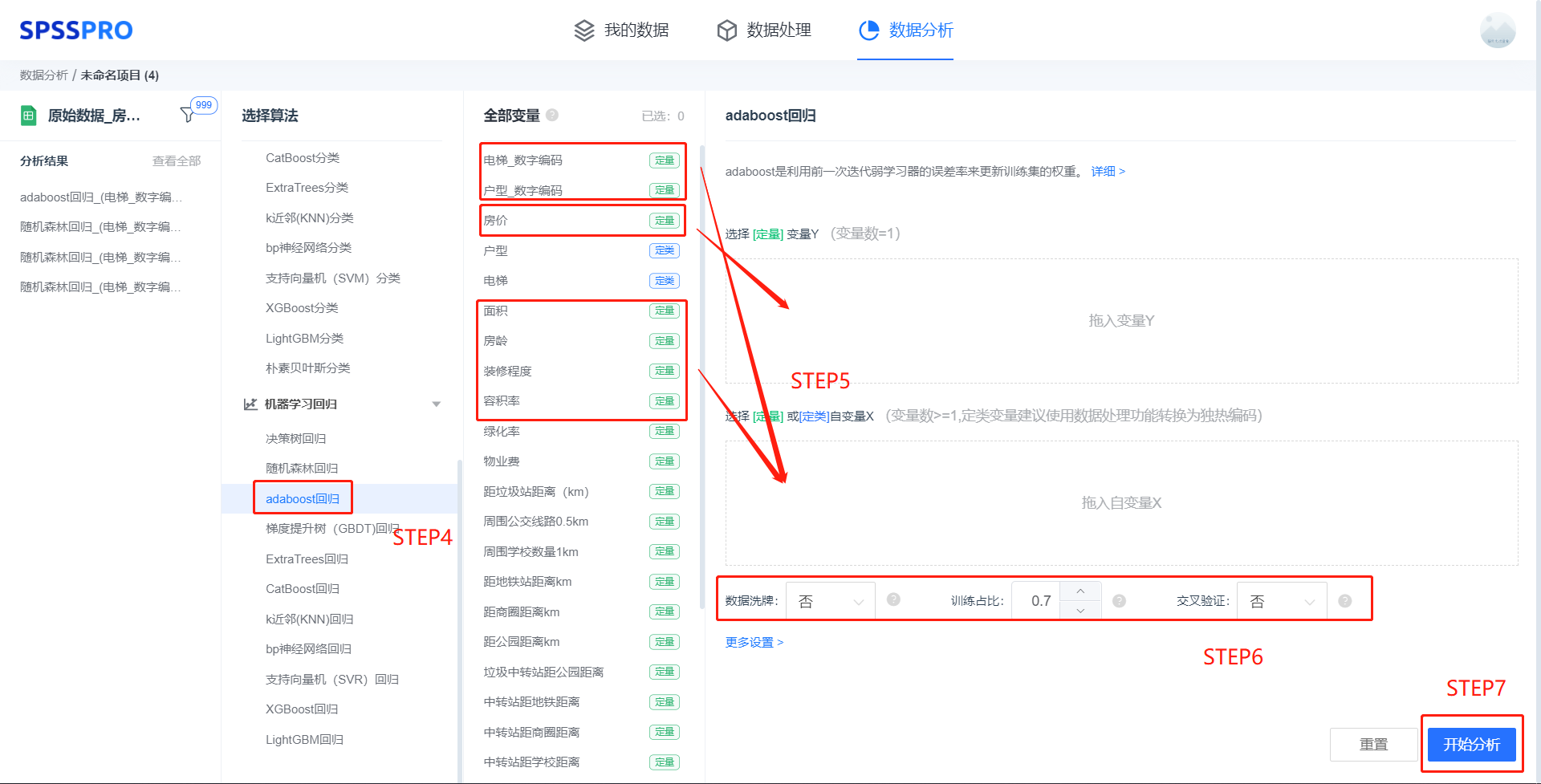

step4：选择【adaboost回归】；
step5：查看对应的数据数据格式，按要求输入【adaboost回归】数据(注：定类变量建议进行编码);
step6：进行参数设置（“更多设置”里的参数在客户端可进行设定）
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：模型参数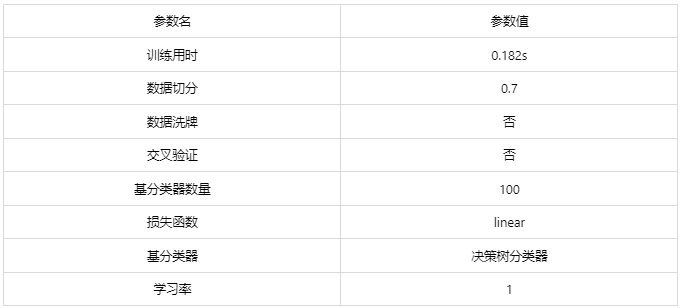

图表说明：上表展示了训练该模型的时候，输入的参数以及训练所耗的时间。

输出结果2：特征重要性

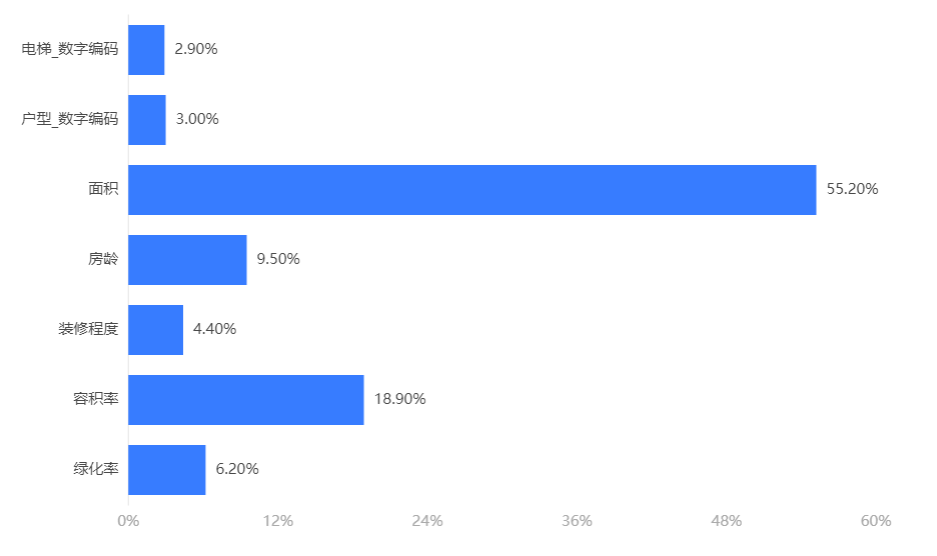
图表说明：上柱形图或表格展示了各特征（自变量）的重要性比例。(附：有时候可以利用特征重要性反推该变量在实际生活中的价值，因为该重要性往往决定结果。)
分析：面积、容积率和房龄是决定房价的重要因素。

输出结果3：模型评估结果

图表说明：上表中展示了交叉验证集、训练集和测试集的预测评价指标，通过量化指标来衡量决策树的预测效果。其中，通过交叉验证集的评价指标可以不断调整超参数，以得到可靠稳定的模型。
● MSE（均方误差）：预测值与实际值之差平方的期望值。取值越小，模型准确度越高。
● RMSE（均方根误差）：为MSE的平方根，取值越小，模型准确度越高。
● MAE（平均绝对误差）：绝对误差的平均值，能反映预测值误差的实际情况。取值越小，模型准确度越高。
● MAPE（平均绝对百分比误差）：是 MAE 的变形，它是一个百分比值。取值越小，模型准确度越高。
● R²：将预测值跟只使用均值的情况下相比，结果越靠近 1 模型准确度越高。
● oob_score：对于回归问题，oob_score是袋外数据的R²。若在建立树过程中选择有放回抽样时，大约1/3的记录没有被抽取。没有被抽取的自然形成一个对照数据集，可用于模型的验证。所以随机森林不需要另外预留部分数据做交叉验证，其本身的算法类似交叉验证，而且袋外误差是对预测误差的无偏估计。（当算法参数选择了“袋外测试数据”后，才会通过oob_score来检验模型的泛化能力）
分析：
训练集中R方为0.964，测试集中为0.952，拟合效果优秀。

输出结果4：测试数据预测结果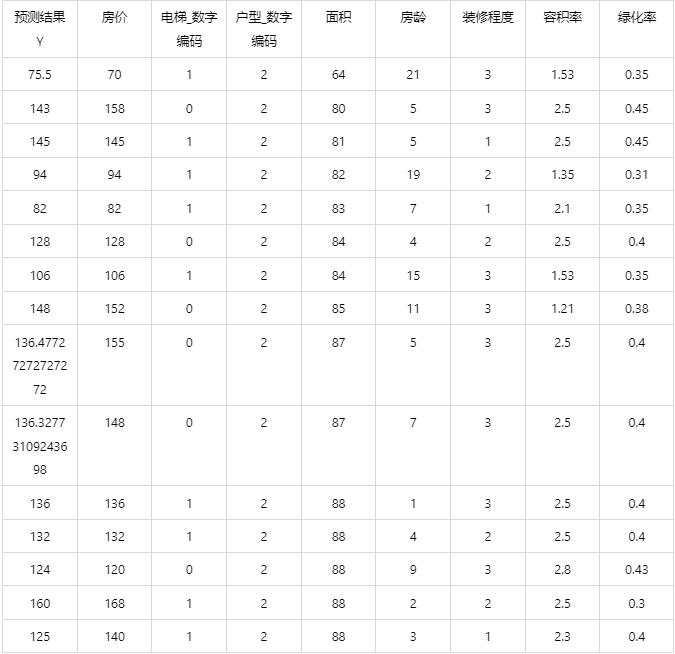

图表说明：上表展示了adaboost模型对测试数据的预测情况。

输出结果5：测试预测图

图表说明：上图中展示了adaboost模型对测试数据的预测情况。

输出结果6：模型预测与应用（此功能只在客户端支持使用）
注：当无法进行预测功能时，可检查数据集中是否存在定类变量或者缺失值：
●当存在定类变量时，请在用于训练模型的数据集和用于预测的数据集中将变量编码，再进行操作。
（SPSSPRO：数据处理->数据编码->将定类变量编码为定量）
●当用于预测数据的数据集中存在缺失值时，请删去缺失值再进行操作。
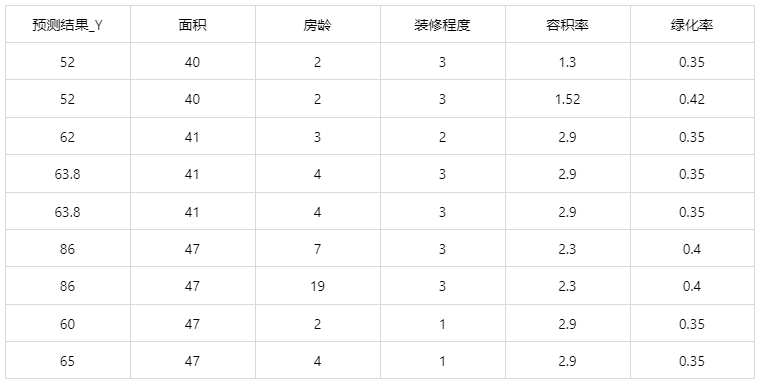
情况1：在上面模型评估后，若具有实用性，这时我们可将该模型进行应用。点击【模型预测】上传文件可以直接得到预测结果。

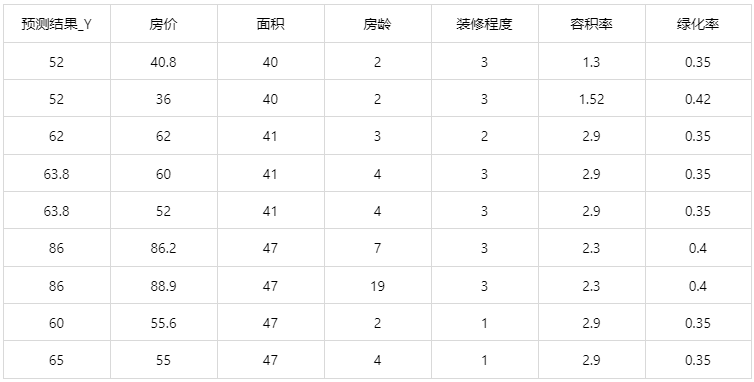
情况2：若是上传的数据包括因变量真实值，不仅仅可以得到预测结果，还可以得到评价效果。

# 7、注意事项

由于adaboost具有随机性，每次运算的结果不一样。若需要保存本次训练模型，需要使用SPSSPRO客户端进行。
adaboost的参数修改需要使用SPSSPRO客户端进行。

# 8、模型理论

AdaBoost，是英文"Adaptive Boosting"（自适应增强）的缩写，是一种机器学习方法，由Yoav Freund和Robert Schapire提出。AdaBoost方法的自适应在于：前一个分类器分错的样本会被用来训练下一个分类器。AdaBoost方法对于噪声数据和异常数据很敏感。但在一些问题中，AdaBoost方法相对于大多数其它学习算法而言，不会很容易出现过拟合现象。AdaBoost方法中使用的分类器可能很弱（比如出现很大错误率），但只要它的分类效果比随机好一点（比如两类问题分类错误率略小于0.5），就能够改善最终得到的模型。而错误率高于随机分类器的弱分类器也是有用的，因为在最终得到的多个分类器的线性组合中，可以给它们赋予负系数，同样也能提升分类效果。
AdaBoost方法是一种迭代算法，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率。每一个训练样本都被赋予一个权重，表明它被某个分类器选入训练集的概率。如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。通过这样的方式，AdaBoost方法能“聚焦于”那些较难分（更富信息）的样本上。
在具体实现上，最初令每个样本的权重都相等，对于第k次迭代操作，我们就根据这些权重来选取样本点，进而训练分类器Ck。然后就根据这个分类器，来提高被它分错的的样本的权重，并降低被正确分类的样本权重。然后，权重更新过的样本集被用于训练下一个分类器Ck。整个训练过程如此迭代地进行下去。

算法实现：
用xi和yi表示原始样本集D的样本点和它们的类标。用Wk(i)表示第k次迭代时全体样本的权重分布。这样就有如下所示的AdaBoost算法：

初始化：输入参数为训练集D={x1，y1，...，xn，yn}，最大循环次数kmax，采样权重Wk(i)=1/n，i=1，...，n；
迭代计数器k赋值为0；
计数器k自增1；
使用Wk(i)采样权重对弱学习器Ck进行训练；
对弱学习器Ck的训练结果进行评估并记录进误差矩阵Ek中；
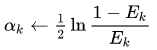
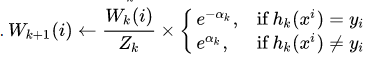
当k=kmax时停止训练
返回结果 Ck和αk，k=1，...，kmax（带权值分类器的总体）
结束

注意第5行中，当前权重分布必须考虑到分类器Ck的误差率。在第7行中，Zk只是一个归一化系数，使得Wk(i)能够代表一个真正的分布，而hk(xi)是分量分类器Ck给出的对任一样本点xi的标记（+1或-1），hk(xi) = yi时，样本被正确分类。第8行中的迭代停止条件可以被换为判断当前误差率是否小于一个阈值。
最后的总体分类的判决可以使用各个分量分类器加权平均来得到：

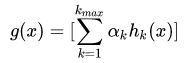
这样，最后对分类结果的判定规则是：

#
9、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]Freund, Yoav; Schapire, Robert E. A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting. 1995. CiteSeerX: 10.1.1.56.9855.
[3]O. Duda, Peter E. Hart, David G. Stork, Pattern Classification, 2nd Edition, Wiley, 2000, ISBN 978-0-471-05669-0

建议反馈