K近邻(KNN)回归

操作视频

SPSSPRO教程-K近邻(KNN)回归

# 1、作用

k 近邻算法，是将 K 个最近邻实例进行平均处理预测的一种有监督算法。

# 2、输入输出描述

输入：自变量 X 为 1 个或 1 个以上的定类或定量变量，因变量 Y 为一个定量变量。
输出：模型输出的结果值及模型预测效果。

# 3、案例示例

研究“幸福感”的影响因素，有四个变量可能对幸福感有影响，他们分别是：经济收入、受教育程度、身体健康、情感支持。建立 knn 回归模型来预测幸福度。

# 4、案例数据

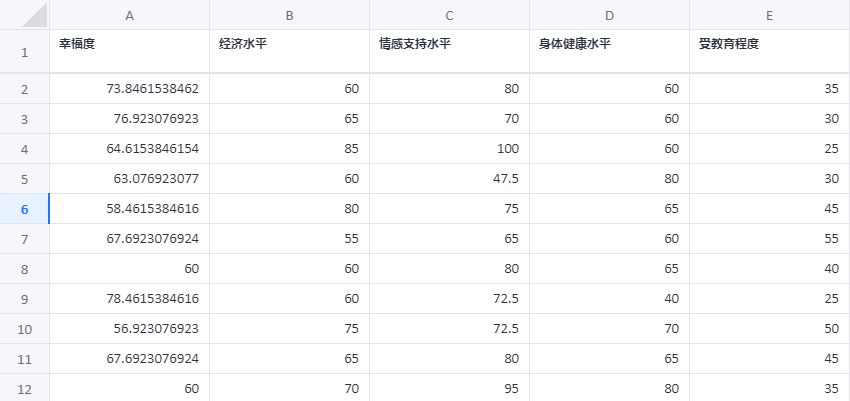
KNN 回归案例数据

# 5、案例操作

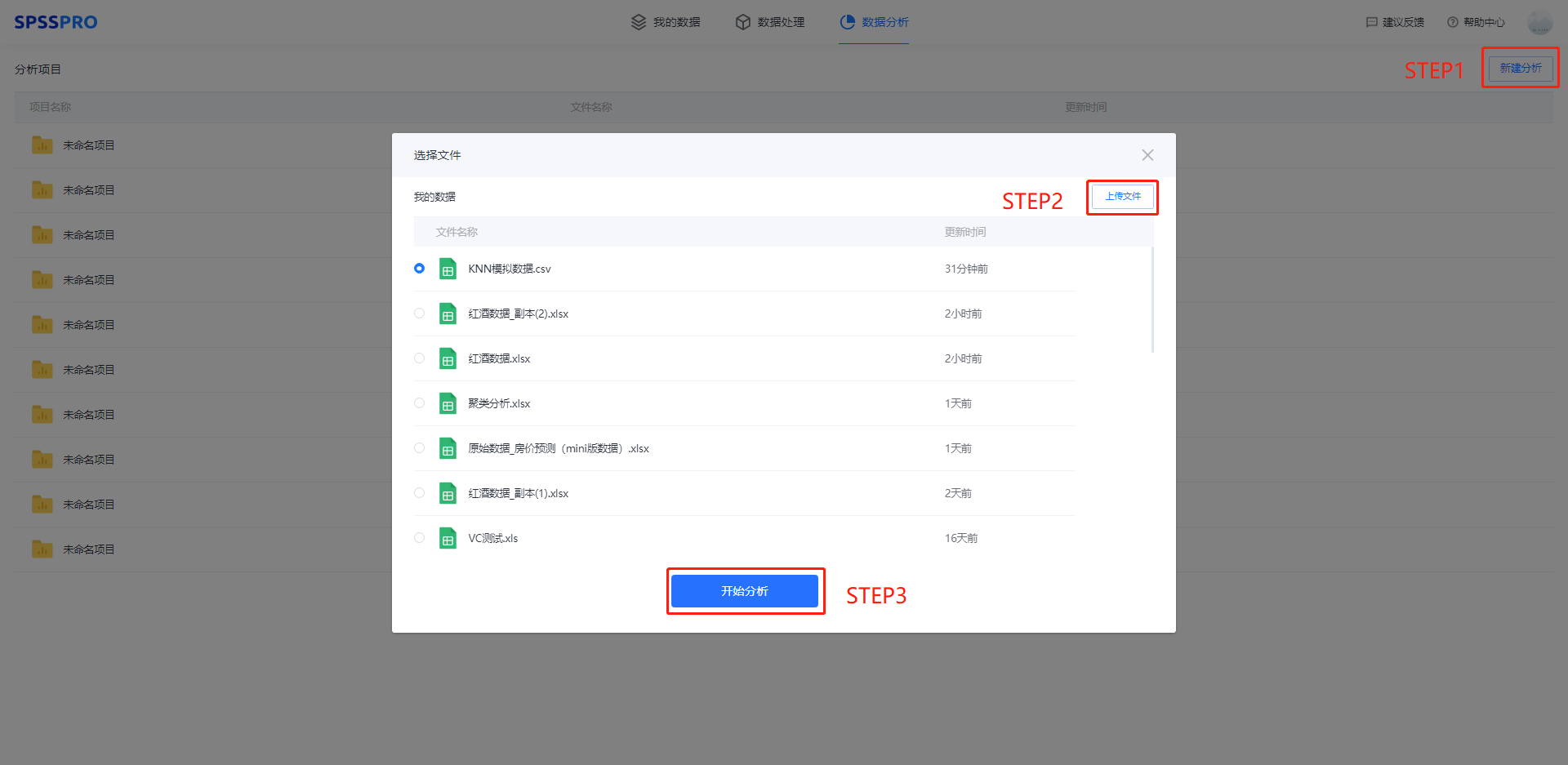
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；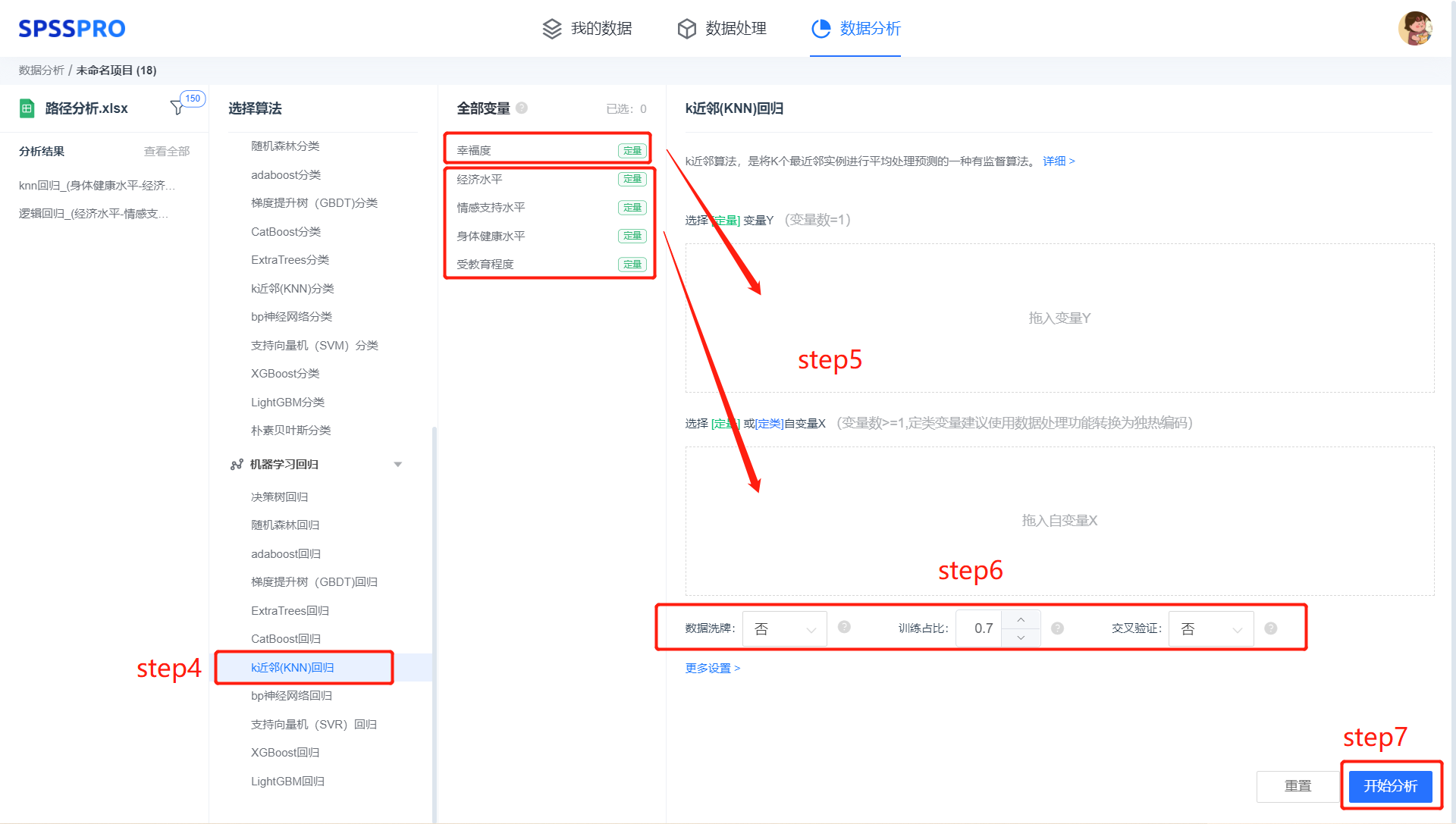

step4：选择【K 近邻回归】；
step5：查看对应的数据数据格式，按要求输入【K 近邻回归】数据(注：K 近邻中定类自变量建议进行编码,定量变量建议标准化);
step6：进行参数设置（“更多设置”里的参数在客户端可进行设定）
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：模型参数

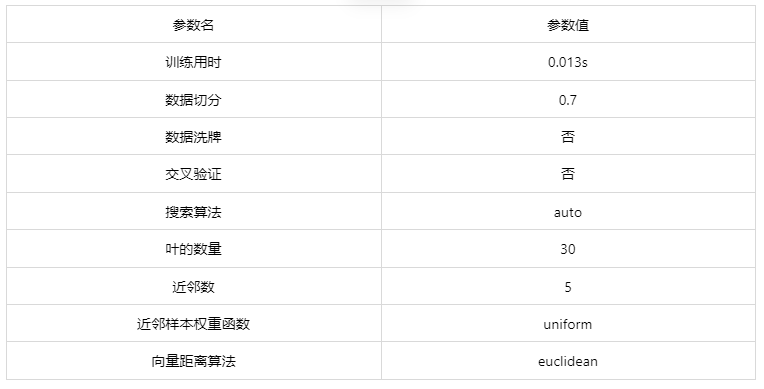
图表说明：上表展示了训练该模型的时候，输入的参数以及训练所耗的时间。

输出结果 2：模型评估结果

图表说明：上表中展示了训练集和测试集的预测评价指标，通过量化指标来衡量 k 近邻(KNN)的预测效果。
● MSE（均方误差）：预测值与实际值之差平方的期望值。取值越小，模型准确度越高。
● RMSE（均方根误差）：为 MSE 的平方根，取值越小，模型准确度越高。
● MAE（平均绝对误差）：绝对误差的平均值，能反映预测值误差的实际情况。取值越小，模型准确度越高。
● MAPE（平均绝对百分比误差）：是 MAE 的变形，它是一个百分比值。取值越小，模型准确度越高。
● R²：将预测值跟只使用均值的情况下相比，结果越靠近 1 模型准确度越高。
分析：
训练集测试集的各预测评价指标值相差不大，就平均绝对百分比误差来看，误差率仅 8%左右，模型预测良好。

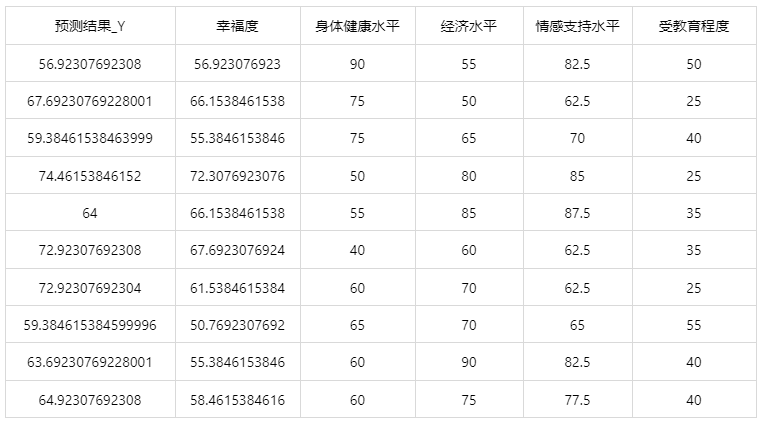
输出结果 3：测试数据预测结果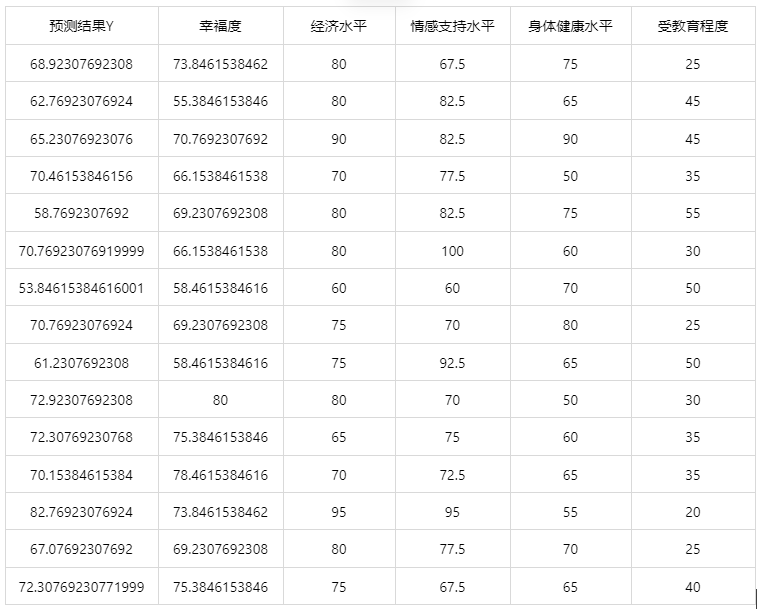

图表说明：上表格为预览结果，只显示部分数据，全部数据请点击下载按钮导出。
上表展示了 K 近邻模型对测试数据的预测结果，第一列是预测结果，第二列是因变量真实值，其余列是各自变量的值。

输出结果 4：测试数据预测图

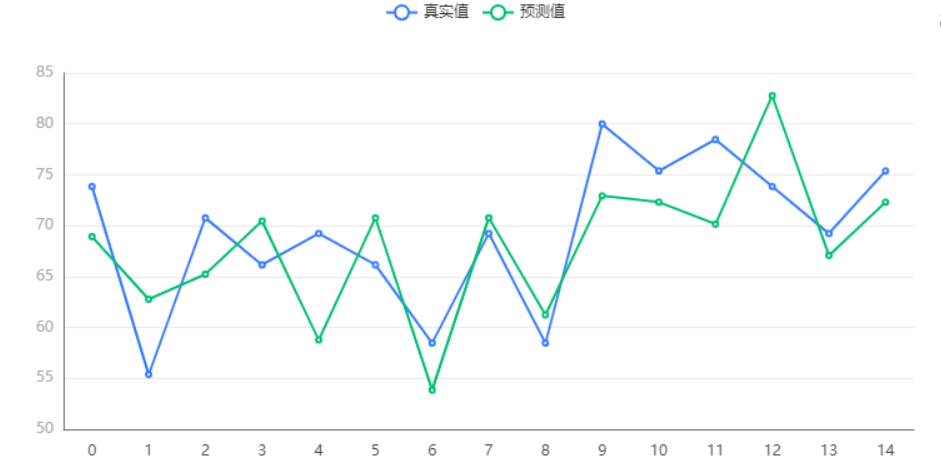
图表说明：上图中展示了 K 近邻回归对测试数据的预测情况。

输出结果 5：模型预测与应用（此功能只在客户端支持使用）
注：当无法进行预测功能时，可检查数据集中是否存在定类变量或者缺失值：
● 当存在定类变量时，请在用于训练模型的数据集和用于预测的数据集中将变量编码，再进行操作。
（SPSSPRO：数据处理->数据编码->将定类变量编码为定量）
● 当用于预测数据的数据集中存在缺失值时，请删去缺失值再进行操作。

情况 1：在上面模型评估后，模型分类结果较好，具有实用性，这时我们将该模型进行应用。点击【模型预测】上传文件可以直接得到预测结果。

经上述操作后，得到以下结果：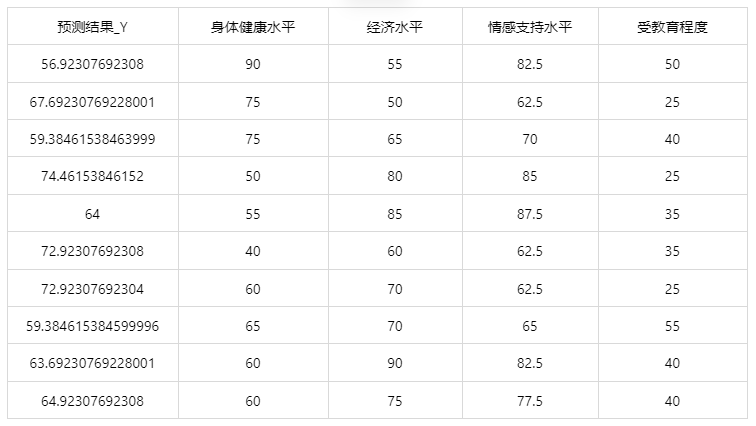

情况 2：若是上传的数据包括因变量真实值，不仅仅可以得到预测结果，还可以得到当前应用数据预测评估效果。

经上述操作后，得到以下结果：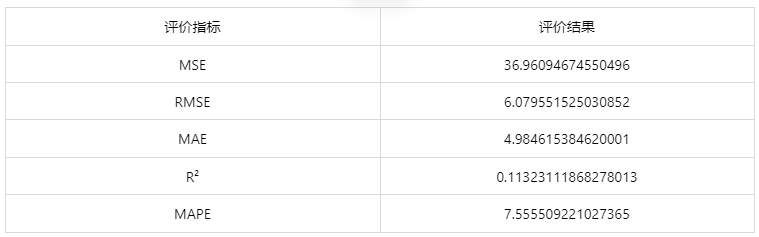

# 7、注意事项

若在训练划分时对数据进行洗牌打乱数据顺序，会导致 K 近邻具有随机性，每次运算的结果不一样。若需要保存本次训练模型，需要使用 SPSSPRO 客户端进行。
K 近邻的参数修改需要使用 SPSSPRO 客户端进行。

# 8、模型理论

KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同。KNN做分类预测时，一般是选择多数表决法，即训练集里和预测的样本特征最近的K个样本，预测为里面有最多类别数的类别。KNN做回归时，一般是选择平均法，即最近的K个样本的样本输出的平均值作为回归预测值。但它们的理论是一样的。
模型介绍：
K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的平均值作为预测值。
看一个最简单的例子，当k=1时，即新实例的类别由里它最近的训练实例的值决定。当k=3时，预测值为最近三个训练样本的值求平均；当k=5时，预测值为最近三个训练样本的值求平均。这里面“最近距离”的定义，是由距离公式求出来的值。

K 值的选取：
如何选择一个最佳的 K 值取决于数据。一般情况下，在分类时较大的 K 值能够减小噪声的影响，但会使类别之间的界限变得模糊。一个较好的 K 值能通过各种启发式技术来获取。
在二元（两类）分类问题中，选取 k 为奇数有助于避免两个分类平票的情形。在此问题下，选取最佳经验 k 值的方法是自助法(Bootstrap)。

距离公式：
这里面“最近距离”来的定义，是由距离公式求出来的值。距离度量除了常用的欧式距离，还可以使用曼哈顿距离和切比雪夫距离。

求解算法：
既然我们要找到 k 个最近的邻居来做预测，那么我们只需要计算预测样本和所有训练集中的样本的距离，然后计算出最小的 k 个距离即可，接着多数表决，很容易做出预测。这个方法的确简单直接，在样本量少，样本特征少的时候有效。但是在实际运用中很多时候用不上，为什么呢？因为我们经常碰到样本的特征数有上千以上，样本量有几十万以上，如果我们这要去预测少量的测试集样本，算法的时间效率很成问题。因此，这个方法我们一般称之为蛮力实现。比较适合于少量样本的简单模型的时候用。
蛮力实现在特征多，样本多的时候很有局限性，我们可以选择 KD 树或者球树来实现。

#
9、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]Hall P, Park BU, Samworth RJ. Choice of neighbor order in nearest-neighbor classification. Annals of Statistics. 2008, 36 (5): 2135–2152. doi:10.1214/07-AOS537.
[3]Everitt, B. S., Landau, S., Leese, M. and Stahl, D.（2011）Miscellaneous Clustering Methods, in Cluster Analysis, 5th Edition, John Wiley & Sons, Ltd, Chichester, UK.

建议反馈