# 数据变换

# 1、作用

数据变换是将数据转换成更适合数据分析的形式。是指通过某种数学方法或函数，对原始数据进行转换或处理，以达到改善数据特性、减少数据噪声、增强模型性能或符合模型假设的目的。其中 Box-Cox 变换的目的是为了让数据满足线性模型的基本假定。而小波变换和傅里叶变换能有效地提取相关的数据进行：小波变换可以同时提取时域信息和频域信息，而傅里叶变换只能提取频域信息。

# 2、输入输出描述

输入：一项定量。
输出：变换后的新序列。

# 3、案例示例

案例：对于非正态数据，使用 Box-Cox 变换从而使得数据分布服从正态分布。而对于噪声数据，使用小波变换对数据进行降噪。

# 4、案例数据

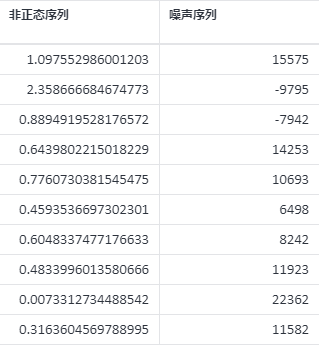
数据变换案例数据

# 5、案例操作

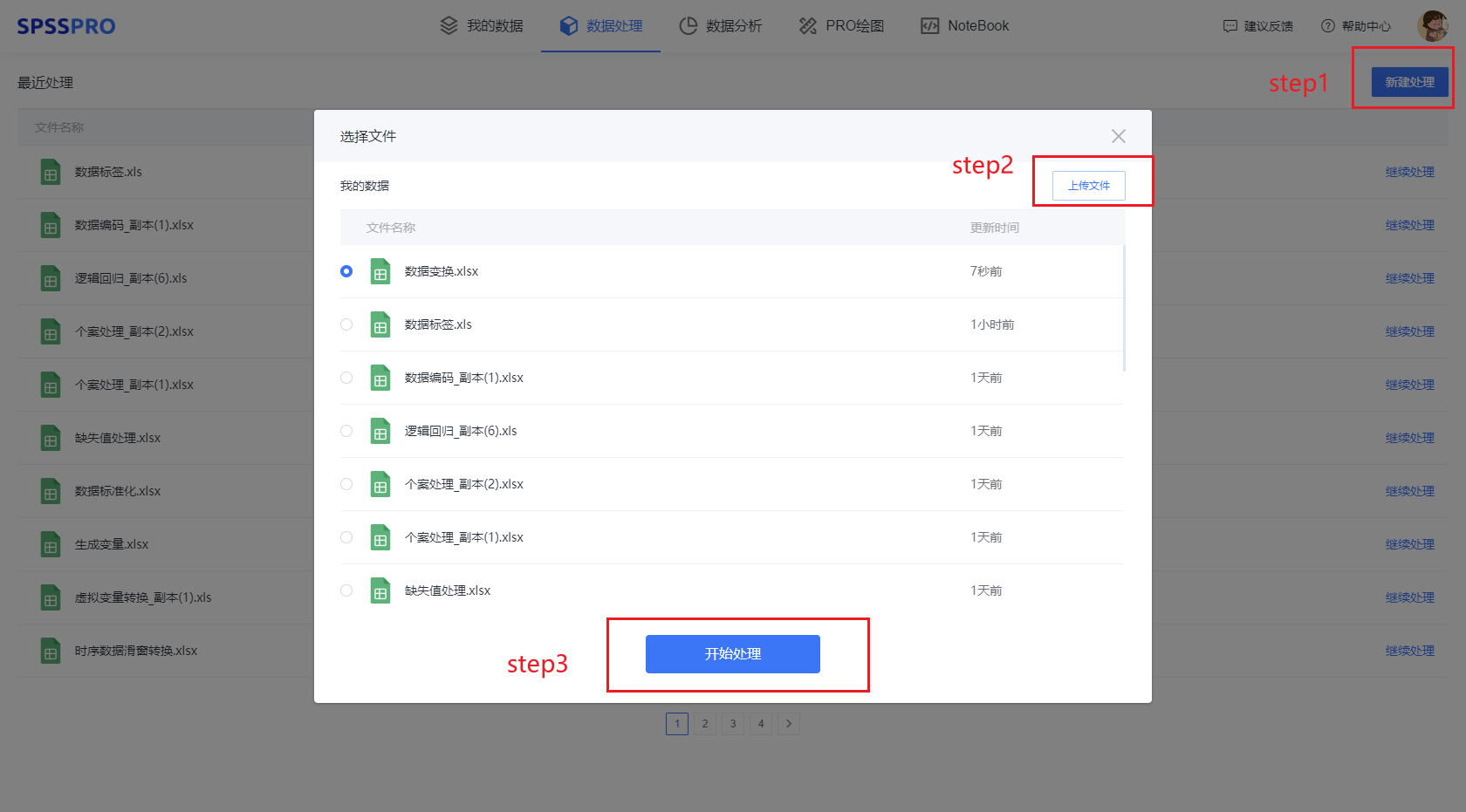
Step1：在“数据处理”模块新建处理；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始处理；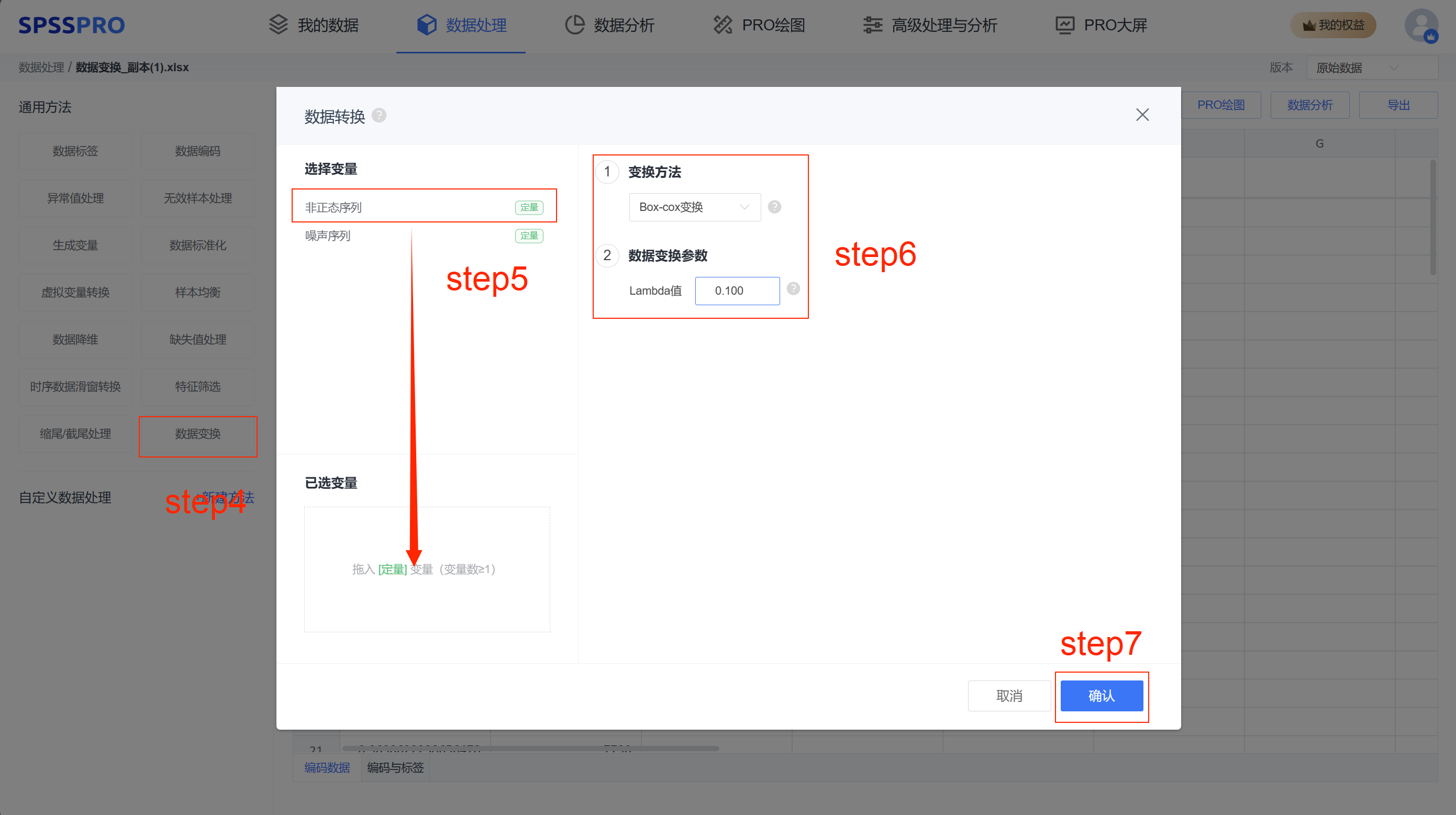

step4：选择【数据变换】；
step5：查看对应的数据数据格式，【数据变换】要求变量为定量变量，且至少有一项；
step6：确认参数，存在 box-cox 变换和小波变换。
step7：点击【开始处理】，完成全部操作。

# 6、输出结果分析

这里以 box-cox 变换为例，可以看到，变换前的数据不满足正态分布；变换后的数据满足正态分布。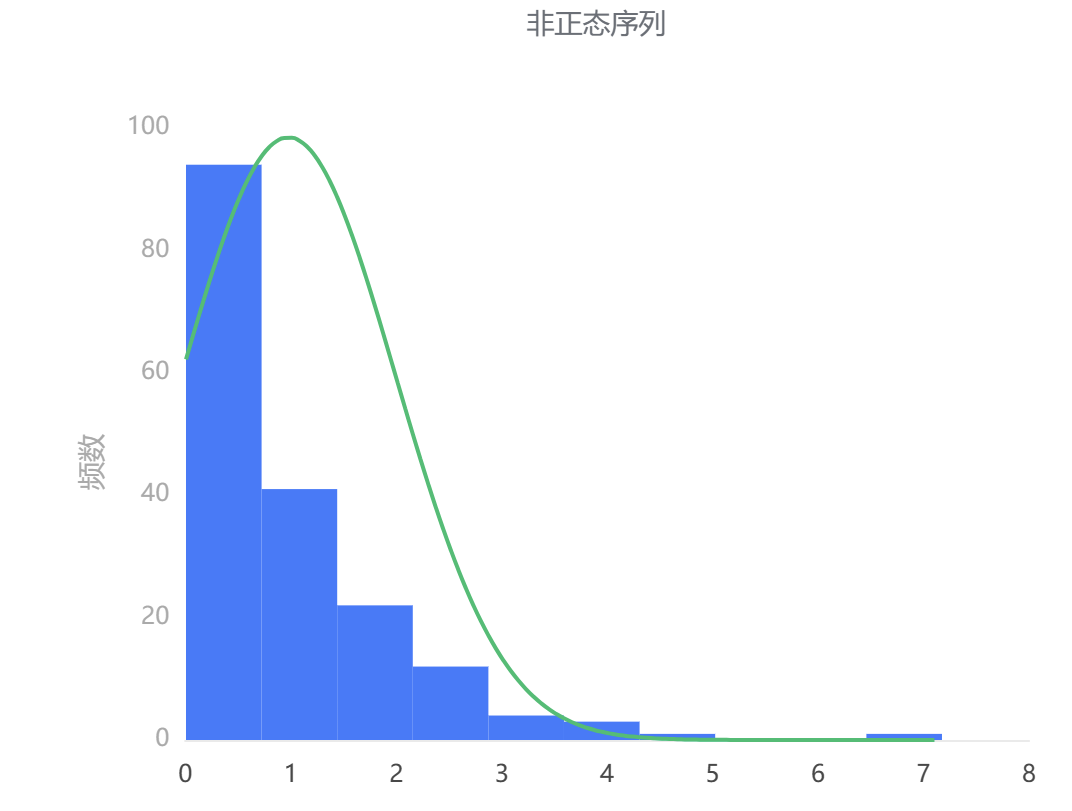

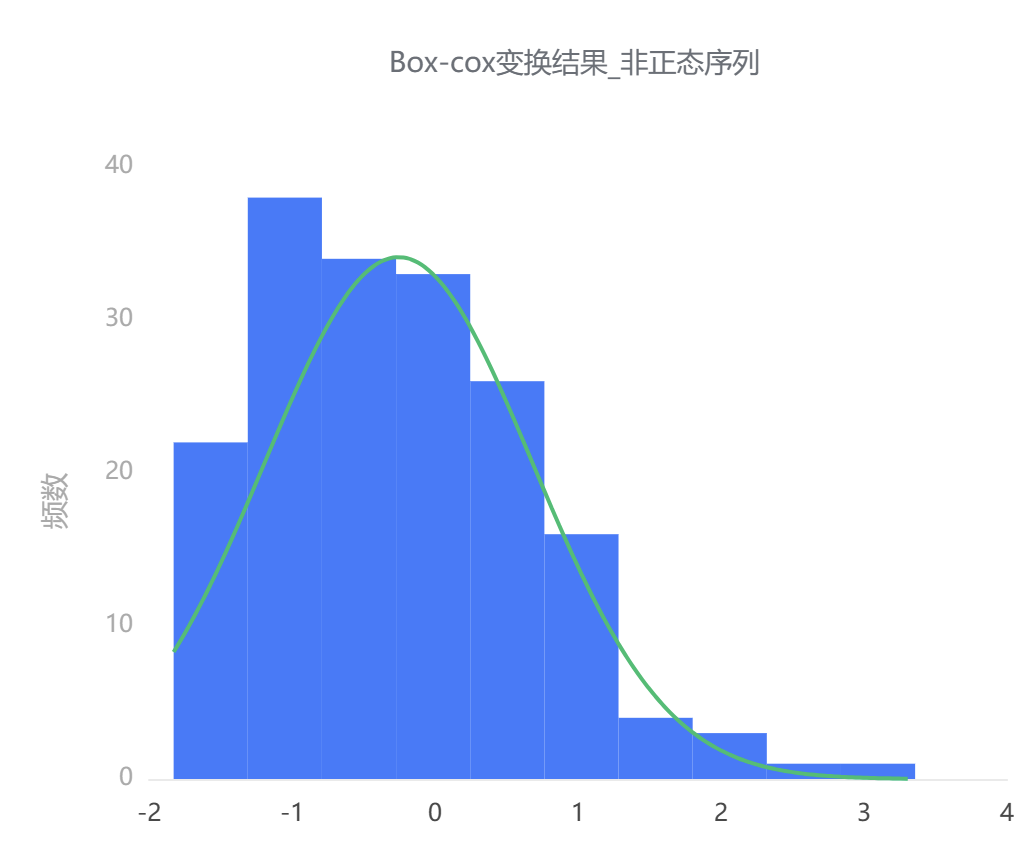
# 7、注意事项

• 数据变换不支持对存在空值的变量进行处理，需要提前处理空值。

# 8、模型理论

# 傅里叶变换

傅里叶变换是一种将函数展开为三角函数的和或者积分的分析方法。常用于信号处理、通信、图像处理等领域。傅里叶变换只能提取频域信息。

在信号去噪中，其基本思想是将含噪声的信号进行傅里叶变换，得到频域图谱。然后使用低通或带通滤波器滤除噪声频率，再通过逆傅里叶变换恢复信号。傅里叶变换的结果是一个复数，其模可以提取频域信息。

傅里叶变换的目的是将时域（即时间域）上的信号转换为频域（即频率域）上的信号。因此，对于同一个信号，从不同的域进行分析可以提供不同的角度和处理方法。在时域中难以处理的问题，可以在频域中更容易解决。对时域信号$x(t)$进行变换：

$$X(f)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}x(t)e^{-j2\pi ft}dt$$

其中，$X(f)$是频域表示，$f$是频率。

# 傅里叶逆变换

傅里叶逆变换（Inverse Fourier Transform）将频域中的信号恢复到时域（或空间域），实现从频域到时域的反转换，可以在数据经过降噪或其他处理后使用。对频域信号$X(f)$进行逆变换：

$$x(t)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}X(f)e^{j2\pi ft}df$$

其中，$x(t)$是时域信号。

# Box-cox 变换

Box-Cox 变换是一种广义幂变换方法，用于处理定量变量不满足正态分布的情况。其主要目的是通过引入参数$\lambda$，使数据变换后更接近于正态分布，从而满足线性模型的基本假设，包括线性关系、正态性和方差齐性。在应用 Box-Cox 变换之前，数据必须为非负数。如果数据不满足这一条件，可以通过加上一个固定值来确保数据为非负数。Box-Cox 变换通常用于处理数据的偏斜性和方差不稳定性，是统计分析中常见的预处理方法。

给定一组正数或非负数$\{x_i\}$，Box-Cox 变换可以通过以下公式进行：

$$y_i=\{\begin{array}{ll}\frac{x_i^{\lambda }-1}{\lambda },& \text{if }\lambda \ne 0\\ \ln (x_i),& \text{if }\lambda =0\end{array}$$

# Box-cox 逆变换

Box-cox 的逆变换，在使用 Box-cox 变换后的数据建立模型后，将使用模型进行预测的预测值逆变换可以得到原先分布的结果。其中$\lambda$值需要与先前使用 Box-cox 的$\lambda$值一致，如果进行 Box-Cox 变换时对数据进行了平移以保证非负性（如 $x_i+\text{const}$），在逆变换时也需相应地调整。

逆变换即是从$y_i$ 到 $x_i$ 的反向操作。具体来说， 逆变换公式为：

$$x_i=\{\begin{array}{ll}{(y_i\cdot \lambda +1)}^{1/\lambda },& \text{if }\lambda \ne 0\\ e^{y_i},& \text{if }\lambda =0\end{array}$$

# 连续小波变换

连续小波变换（Continuous Wavelet Transform，CWT）能够将信号或图像转换到时频域中，提供时间和频率的局部信息。它是一种将信号函数通过一系列小波函数的叠加展开的变换分析方法，具有多分辨率分析的特点，能够有效地捕捉信号的局部特征。相比于傅里叶变换，CWT克服了难以表征信号局部特征的局限性。连续小波变换可以捕捉信号的局部特征，适用于分析非平稳信号和时变信号的频谱信息。目前支持的一级小波分解可直接得到降噪后的变换序列。其具体步骤为：

• 1. 选择适当的小波函数（母小波）和尺度参数。
• 2. 对信号$x(t)$进行连续小波变换：

$$W(a,b)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}x(t){\psi }_{a,b}(t)dt$$

其中，${\psi }_{a,b}(t)$是小波函数，$a$是尺度函数，$b$是平移参数。

# 离散小波变换

离散小波变换（Discrete Wavelet Transform，DWT）类似于连续小波变换，但是它使用离散信号和基函数来将信号分解成不同频率带的近似和详细信息。为了更好地利用计算机进行处理，离散小波变换必须对信号进行离散化处理，其结果是离散的小波变换系数，用于表示尺度和平移因子的离散值。离散小波变换主要用于提取信号的频域信息。

目前支持的一级小波分解可以直接得到经过降噪处理后的变换系列。离散小波变换广泛应用于信号压缩、噪声去除和特征提取，尤其在图像处理、数据压缩和模式识别等领域。其具体步骤如下：

• 1. 选择小波基函数（如 Haar、Daubechies 等）和分解层数。
• 2. 对离散信号$x[n]$进行离散小波变换，得到近似系数$A$和详细函数$D$。

$$W_j(n)=\sum _{k}x[k]\cdot {\varphi }_{j,k}(n)$$

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.