特征筛选

# 特征筛选

# 1、作用

特征筛选是一个至关重要的预处理步骤。随着数据集的日益庞大和复杂，特征的数量往往也随之激增。然而，并非所有的特征都对模型的性能提升有所贡献，有些特征甚至可能是冗余的、噪声较大的或者与目标变量无关的。特征数过多一方面增加了模型的复杂度，另一方面特征多也引入了更多的噪声数据，使模型更容易学到噪声，增大了发生过拟合的风险。所以变量（特征）过多时，需要从原始特征中选择出一些最有效特征以降低数据维度，从而有效提高模型性能。

特征筛选的重要性主要体现在：1. 减少模型的复杂度，降低过拟合的风险；2.专注于对预测结果有影响的特征，加速训练过程，提高模型的性能；3.提高模型的解释性。

# 2、输入输出描述

输入：至少两项定量变量。
输出：在变量名后标明应保留还是应剔除。

# 3、案例示例

案例：现有八个变量，通过特征筛选选出较为有效的特征。

# 4、案例数据

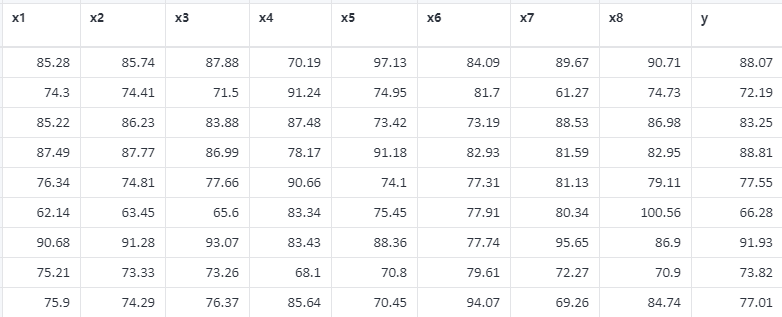
特征筛选案例数据

# 5、案例操作

Step1：在“数据处理”模块新建处理；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始处理；

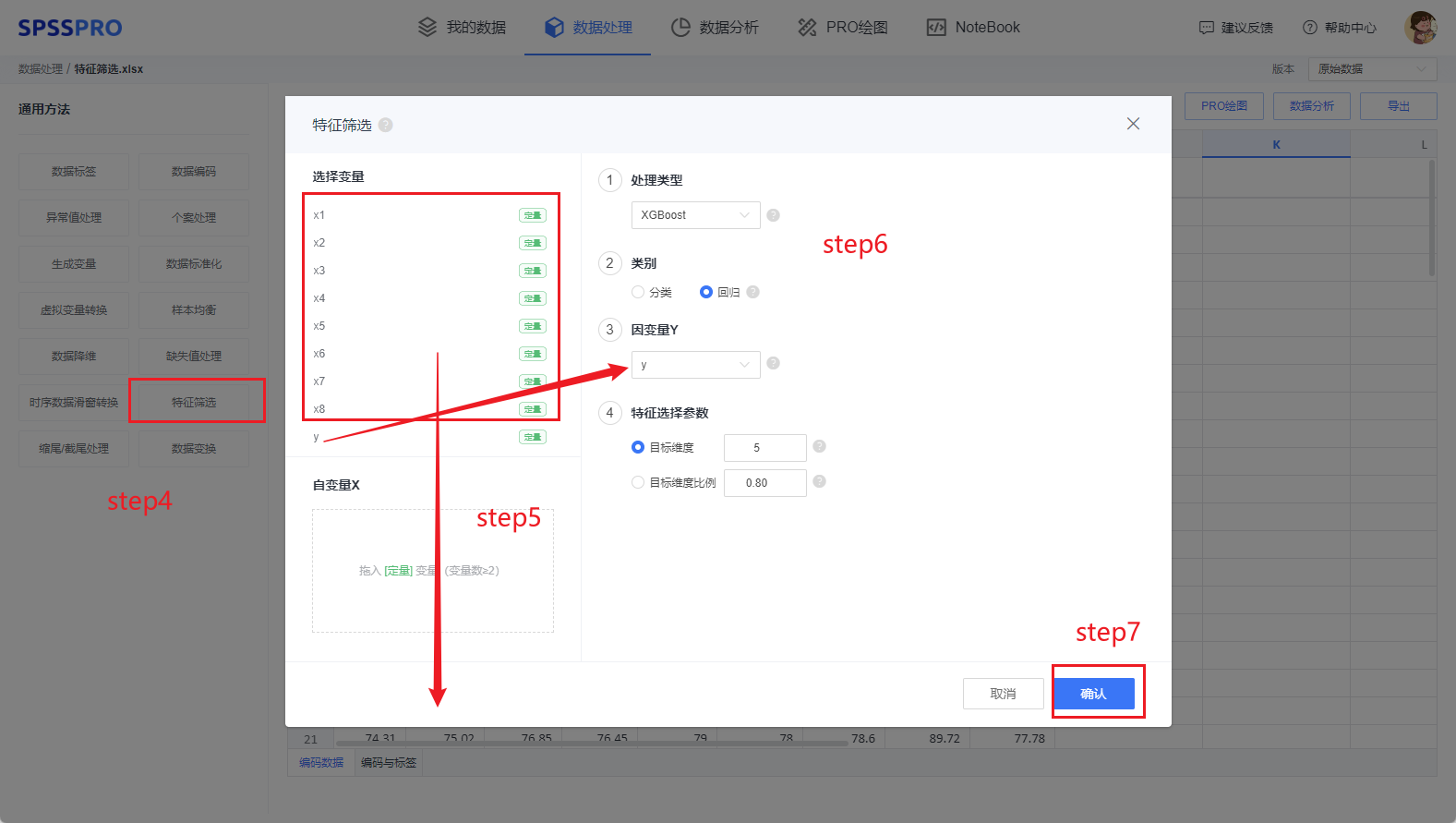
Step4：选择【特征筛选】；
Step5：查看对应的数据数据格式，【特征筛选】要求变量为定量变量，且至少有两项；
Step6：确认参数，有多种特征筛选方法可选择；
Step7：点击【开始处理】，完成全部操作。

# 6、输出结果分析

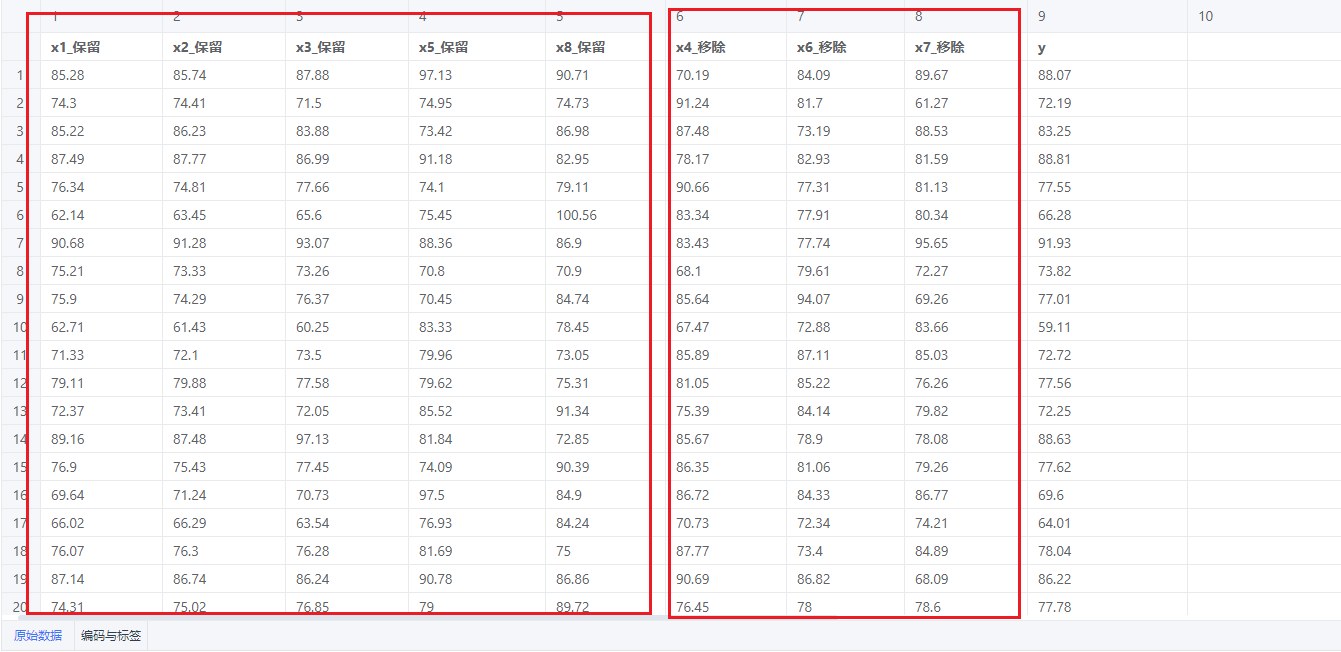
对于刚刚我们选中的8个变量，选用xgboost方法，即自变量和因变量建立一个XGBoost回归模型。由于我们自定义目标维度为5，（希望保留5个变量），经过特征筛选后，选取特征重要性较大的前5个变量进行保留，为应保留的的变量和应剔除的变量进行标记，其中，x1、x1、x3、x5、x8这五个变量应该保留，特征比较重要，而x4、x6、x7这三个变量相对来说不那么重要，可以剔除。

# 7、注意事项

特征筛选不支持对存在空值的变量进行处理，需要提前处理空值。
特征筛选功能仅支持在客户端进行使用。

# 8、模型理论

# 方差选择法

方差选择法（Variance Thresholding）是用于过滤掉低方差的特征，从而减少特征值的数量。其核心思想是认为低方差的特征对于模型的预测贡献度较小，因此可以将其移除，以提高模型的效率的减少过拟合的风险。

具体来说，方差选择法的步骤如下：

计算每个特征的方差：对于每一个特征，计算其在整个数据集上的方差。方差衡量了数据的离散程度，即特征值在其均值周围的分布情况。方差大的特征表示数据的变化大，方差小的特征表示数据变化不大，即特征值基本上相同。
设定方差阈值：选择一个合适的方差阈值。通常情况下，我们会根据问题的具体情况或通过实验来确定一个合适的阈值。例如，可以选择一个较小的阈值，如0.1或0.01，以保留方差较大的特征。
过滤特征：移除方差低于设定阈值的特征。这些低方差特征通常被认为对模型预测能力贡献较小，因此移除它们不会显著影响模型的性能，反而可以减少特征空间的维度，提高模型的训练速度。

方差选择法的优点是简单且易于实现，适用于需要快速预处理大规模数据集的情况。然而，需要注意的是，方差选择法忽略了特征之间的相关性，有时可能会移除与目标变量高度相关但方差较小的特征。

# 随机森林特征重要度

随机森林（Random Forest）是一种集成学习算法，基于决策树作为基学习器，通过有放回地抽样训练多棵树，并通过投票等方式来提高模型的预测能力和泛化性能。对于随机森林的模型理论介绍可详见“随机森林分类”板块。

在随机森林中通常使用基尼指数（Gini index）或者袋外数据（Out-Of-Bag data, OOB）错误率来作为评价标准衡量每个特征在随机森林的每棵决策树上的贡献率。

此处讲解以基尼指数作为评价标准筛选特征的过程。

基尼指数：

基尼指数是衡量数据集不纯度（Impurity）的一种指标。基尼指数越小，代表节点的不纯度越低，即样本越倾向于属于同一个类别，即基尼指数我们希望越小越好。

假设一个节点 $t$ 包含样本集合 $D$ ，其中有 $| D |$ 个样本。如果该节点将数据集 $D$ 划分为 $K$ 个类别，基尼指数 $G i n i (t)$ 的计算公式为：

G i n i (t) = 1 - \sum_{i = 1}^{K} p (i | t)^{2}

其中， $p (i | t)$ 是节点 $t$ 中类别 $i$ 的样本的占比。

在决策树的生长过程中，当选择一个特征进行分裂时，会计算基于该特征的基尼指数减少量。该指标衡量了特征在节点分裂中的重要性，即特征能够带来多大程度的不纯度减少。即我们希望该指标越大越好。

对于每个节点 $t$ ，假设使用特征 $A$ 进行分裂，导致左子节点为 $t_{l e f t}$ 和右子节点为 $t_{r i g h t}$
计算使用特征 $A$ 进行分裂后的加权平均基尼指数 $G i n i_s p l i t (A)$ :

G i n i_s p l i t (A) = \frac{| D_{l e f t} |}{| D |} G i n i (t_{l e f t}) + \frac{| D_{R i g h t} |}{| D |} G i n i (t_{R i g h t})

其中， $| D_{l e f t} |$ 和 $| D_{R i g h t} |$ 分别是左右节点的样本数量。

计算基尼指数减少量 $G i n i_g a i n (A)$ :

G i n i_g a i n (A) = G i n i (t) - G i n i_s p l i t (A)

x,h $G i n i_g a i n (A)$ 表示使用特征 $A$ 分裂节点 $t$ 后基尼指数的减少量。

评估特征重要性：对于每个特征 $A$ ，可以通过计算所有决策树中使用特征 $A$ 分裂节点时的平均基尼指数减少量来评估其重要性。

I m p o r t a n c e (A) = \frac{1}{T} \sum_{t = 1}^{T} \sum_{n o d e s u s i n g A} G i n i_g a i n (A)

其中， $T$ 是随机森林中树的数量， $n o d e s u s i n g A$ 表示所有树中使用特征 $A$ 进行节点分裂的节点集合。 $I m p o r t a n c e (A)$ 越高，代表特征 $A$ 对于随机森林的预测越重要。

最后，模型会按照特征重要性对特征（自变量）进行降序排列，保留前几个特征重要性较大的变量。

# XGBoost

XGBoost算法（Extreme Gradient Boosting），即极致梯度提升树，是一种提升树模型，即它将许多树模型集成在一起，形成一个强分类器，并在模型训练中引入了正则化项，降低了过拟合的风险。

在XGBoost中，提升树被创建后，可以相对直接地得到每个特征的重要性得分，特征重要性是通过对数据集中的每个特征进行计算，并进行排序得到。在单个决策树中通过每个特征分裂点改进性能度量的量来计算特征重要性，通常是损失函数的减少量，即特征增益；然后由节点负责加权和记录次数，即一个特征对分裂点改进性能度量越大（越靠近根节点），权值越大；被越多提升树所选择，特征越重要。这里相当于建立了一个xgboost模型，特征变量和因变量是共同参与模型训练的，然后按照特征重要性对特征（自变量）进行降序排列，保留前几个特征重要性较大的变量。

从数学角度来看，大致推导如下：

根据Boosting的原理可得，第 $t$ 棵树对样本 $i$ 的预测值 = 前 $t - 1$ 棵树的预测值 + 第 $t$ 棵树的预测值，即：

{\hat{y}}_{i}^{(t)} = {\hat{y}}_{i}^{(t - 1)} + f_{t} (x_{i})

对目标函数 $L^{(t)} = \sum_{i = 1}^{n} l (y_{i}, {\hat{y}}_{i}^{(t)}) + Ω (f_{t})$ 进行二阶泰勒展开:

L^{(t)} = \sum_{i = 1}^{n} [l (y_{i}, {\hat{y}}_{i}^{(t - 1)}) + g_{i} f_{t} (x_{i}) + \frac{1}{2} h_{i} f_{t}^{2} (x_{i})] + Ω (f_{t})

其中： $Ω (f_{t})$ 是正则化项，表示第 $t$ 棵树的模型复杂度： $Ω (f_{t}) = γ T + \frac{1}{2} λ ∥ w ∥_{2}^{2}$ 。

h_{i} = \frac{\partial^{2} l (y_{i}, {\hat{y}}_{i}^{(t - 1)})}{(\partial {\hat{y}}_{i}^{(t - 1)})^{2}}

因此，我们可以认为，一个样本对于目标函数值的贡献，在于其 $h_{i}$ 。因此可以根据 $h_{i}$ 对特征值的“重要性”进行排序。XGBoost提出了一个新的函数用于表示特征值的“重要性”排名，需要注意的是，这里的特征值是表示某个等待判断分裂的节点属性中的某个取值。

r_{k} (z) = \frac{1}{\sum_{(x, h) \in D_{k}} h} \sum_{(x, h) \in D_{k}, x < z} h

其中， $D_{k}$ ：第 $k$ 个特征的每个样本的特征值 $(x_{n k})$ 与其对应的 $h_{i}$ 组成的集合； $(x_{i k}, h_{i})$ ：表示第 $i$ 个样本对于第 $k$ 个特征的特征值，和其对应的 $h_{i}$ ； $r_{k} (z)$ 的分母：第 $k$ 个特征的所有样本的 $h_{i}$ 的总和； $r_{k} (z)$ 的分子：所有特征值小于 $z$ 的样本的 $h_{i}$ 的总和。

# 相关系数法

相关系数法通过Pearson系数作为特征评分标准，相关系数绝对值越大，相关性越强。这里对每一个自变量和因变量进行Pearson相关性分析，然后按照Pearson系数对特征（自变量）进行降序排列，保留前几个相关系数较大的变量。

假设有两个变量 $X$ 和 $Y$ ，样本大小为 $n$ ，样本均值分别为 $\bar{X}$ 和 $\bar{Y}$ ，则他们的Pearson相关系数 $r_{X Y}$ 为：

r_{X Y} = \frac{\sum_{i = 1}^{n} (X_{i} - \bar{X}) (Y_{i} - \bar{Y})}{\sqrt{\sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}} \cdot \sqrt{\sum_{i = 1}^{n} (Y_{i} - \bar{Y})^{2}}}

$r_{X Y}$ 的取值范围为 $[- 1, 1]$ ；
$r_{X Y} > 1$ ： $X$ 和 $Y$ 正相关；
$r_{X Y} < 1$ : $X$ 和 $Y$ 负相关；
$r_{X Y} = 1$ : $X$ 和 $Y$ 没有线性相关性。

# 互信息法

互信息（Mutual Information，MI）是信息论中一种用来衡量两个随机变量之间关联程度的量。它用来描述一个随机变量中的信息量能否用另一个随机变量的信息量来解释。互信息越大，表示两个随机变量之间的关联程度越高。

给定两个随机变量 $X$ 和 $Y$ ，它们的互信息 $I (X; Y)$ 定义为它们联合分布 $p (X, Y)$ 和各自边缘分布 $p (X)$ 、 $p (Y)$ 之间的关系，计算公式为：

I (X; Y) = \sum_{x \in X} \sum_{y \in Y} p (x, y) \log (\frac{p (x, y)}{p (x) p (y)})

其中， $p (X, Y)$ 是 $X = x$ 且 $Y = y$ 的联合概率分布； $p (X)$ 、 $p (Y)$ 是各自的边缘概率分布； $X$ 和 $Y$ 分别是随机变量 $X$ 和 $Y$ 的取值空间。

MI的特性有：

非负性： $I (X; Y) \geq 0$ 。
对称性： $I (X; Y) = I (Y; X)$ ，即互信息与变量的顺序无关。
信息量单位：通常以比特（bits）为单位，如果使用自然对数的底 $e$ ，则单位为奈特（nats）。

互信息在机器学习、特征选择、信号处理、语言模型等领域中有广泛应用。在特征选择中，互信息可以帮助评估一个特征与目标变量之间的相关性，从而选择最相关的特征进行建模或分析。

# 卡方检验法

卡方检验中我们实际上比较关心的是特征的相对重要性，检验统计量卡方值 $X^{2}$ 越大，越有信心拒绝零假设，接受两个变量不独立的事实，因此我们可以按每个特征的 $X^{2}$ 值的大小进行排序，去除 $X^{2}$ 值小的特征。

x^{2} = \sum \frac{(观 测 频 数 - 期 望 频 数)^{2}}{期 望 频 数} = \sum_{i = 1}^{r o w s} \sum_{j = 1}^{c o l s} \frac{(O_{i, j} - E_{i, j})^{2}}{E_{i, j}}

详细计算和推导可见章节“非参数检验-卡方检验”。

# VIF法

方差膨胀因子(variance inflation factor，VIF)是一种用来评估多重共线性（multicollinearity）的方法，通常应用于线性回归模型中。在特征选择中，VIF可以帮助识别数据集中存在共线性的特征，并据此决定是否需要剔除一些特征以改善模型的解释性和稳定性。

具体而言，对于线性回归模型中的每一个特征 $X_{j}$ 的VIF计算如下：

1.将特征 $X_{j}$ 作为响应变量，用其余的特征来拟合一个线性回归模型：

X_{j} = a_{0} + a_{1} X_{1} + . . . + a_{j + 1} X_{j + 1} + . . . + ϵ

2.计算决定系数 $R_{j}^{2}$ （R-squared）:

R_{j}^{2} = 1 - \frac{S S R}{S S T}

首先根据残差计算残差平方和：

S S R = \sum_{i = 1}^{n} (X_{i j} - {\hat{X}}_{i j})

其中， $n$ 为样本数量， $i$ 为样本的索引。

接着计算总平方和 $S S T$ ：

S S T = \sum_{i = 1}^{n} (X_{i j} - {\bar{X}}_{j})^{2}

其中， ${\bar{X}}_{j}$ 是特征 $X_{j}$ 的样本均值。

需要注意的是， $R_{j}^{2}$ 接近1时，表示特征 $X_{j}$ 可以被其他特征很好地预测，存在较强的多重共线性问题。

计算方差膨胀因子VIF：

V I F_{j} = \frac{1}{1 - R_{j}^{2}}

如果 $V I F_{j} > 某个阈值$ ，常认为存在严重的多重共线性，这时候考虑剔除该特征 $X_{j}$ 。

通常阈值的取值是5或10。

# 递归特征消除法

递归特征消除(Recursive Feature Elimination)的主要思想是反复地训练模型（如随机森林或者回归模型）然后在每一轮训练中剔除对模型贡献较小的特征，从而选出最佳的特征子集。因此，这是一种寻找最优特征子集的贪心算法。

RFE的步骤为：

将需要筛选的 $k$ 个特征（或全特征）作为初始特征子集输入到随机森林分类器中，计算得到每个特征的重要性，并利用交叉验证方法得到初始特征子集的分类精度；
从当前特征子集中移除特征重要性最低的一个特征，得到一个新的特征子集，再次输入到随机森林分类器中，计算新的特征子集中每个特征的重要性，并利用交叉验证方法得到新的特征子集的分类精度。
递归的重复步骤2，直至特征子集为空，最后一共得到 $k$ 个不同特征数量的特征子集，选择分类精度最高的特征子集作为最优特征组合。

从数学层面来看，RFE的工作流程与线性回归模型有关，我们考虑一个最简单的线性回归模型情况，假设有数据集 ${(x_{i}, y_{i})}_{i = 1}^{n}$ ，其中 $x_{i} \in R^{p}$ 是特征向量， $y_{i} \in R$ 是响应变量。

因此，该线性回归模型可以表示为：

y_{i} = β_{0} + \sum_{j = 1}^{p} β_{j} x_{i j} + ϵ_{i}

而我们在训练模型时一般希望得到最小化残差平方和，即：

m i n \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}

其中， ${\hat{y}}_{i} = \hat{β_{0}} + \sum_{j = 1}^{p} \hat{β_{j}} x_{i j}$ 是模型预测值， $\hat{β_{j}}$ 是模型的系数。

如此，在RFE中，会根据当前模型中特征的系数绝对值进行排序，以评估每个特征对模型的贡献度，从而剔除系数较小的特征。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.

建议反馈