# 缺失值处理

# 1、作用

缺失值即空值。数据集不含缺失值的变量被称为完全变量，含有缺失值的变量被称为不完全变量。从缺失的分布来说，我们可以把缺失分为完全随机缺失，随机缺失和完全非随机缺失。

• 完全随机缺失（missing completely at random,MCAR）指的是数据的缺失是完全随机的，不依赖于任何不完全变量或完全变量，不影响样本的无偏性，如家庭地址缺失；

• 随机缺失(missing at random,MAR)：指的是数据的缺失不是完全随机的，即该类数据的缺失依赖于其他完全变量，如财务数据缺失情况与企业的大小有关；

• 非随机缺失(missing not at random,MNAR)：指的是数据的缺失与不完全变量自身的取值有关，如高收入人群不原意提供家庭收入；

对于缺失值，往往直接删除是不合适，于是我们需要进行缺失值处理，包括考虑是否剔除，或进行填充处理。

# 2、输入输出描述

输入：一项或以上定量或定类变量。
输出：对缺失值进行填补后的序列。

# 3、案例示例

案例：示例，现有一个变量，对空值进行识别，并且用当前的均值对空值进行填补。

# 4、案例数据

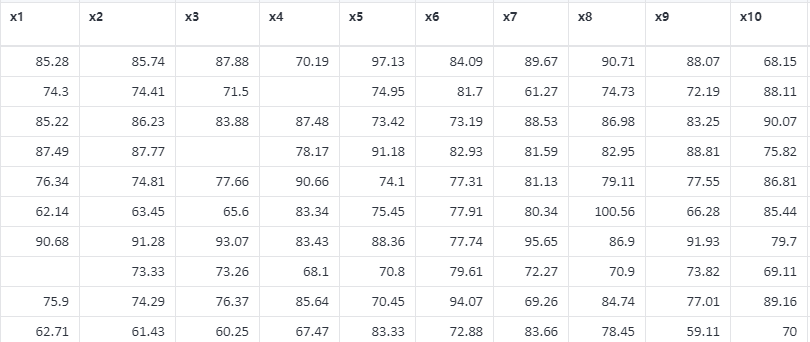
缺失值处理案例数据

# 5、案例操作

Step1：在“数据处理”模块新建处理；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

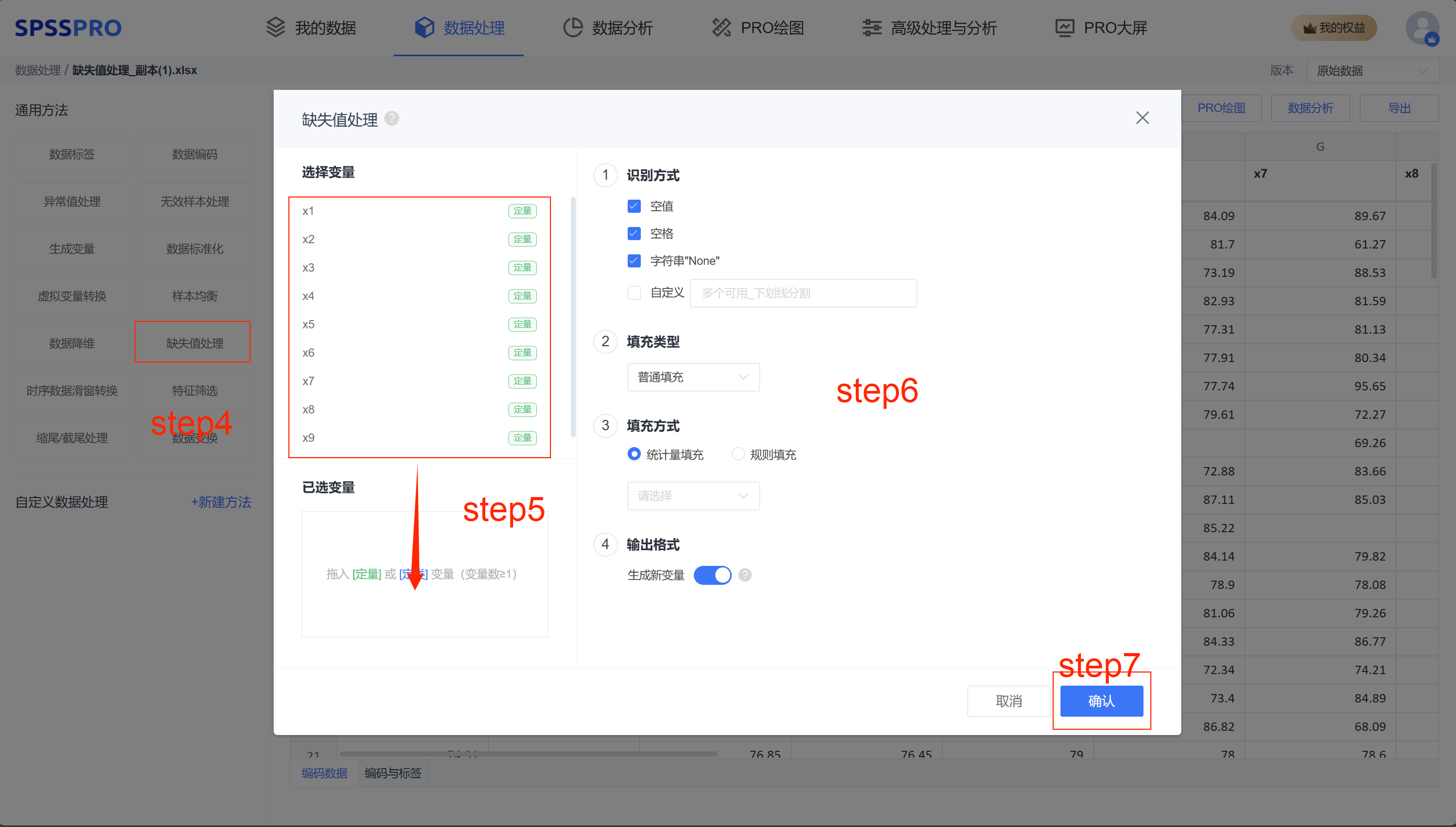
Step4：选择【缺失值处理】；
Step5：查看对应的数据数据格式，【缺失值处理】要求变量为定量或定类变量，且至少有一项；
Step6：确认参数，有不同的填充方法可选择；
Step7：点击【开始处理】，完成全部操作。

# 6、输出结果分析

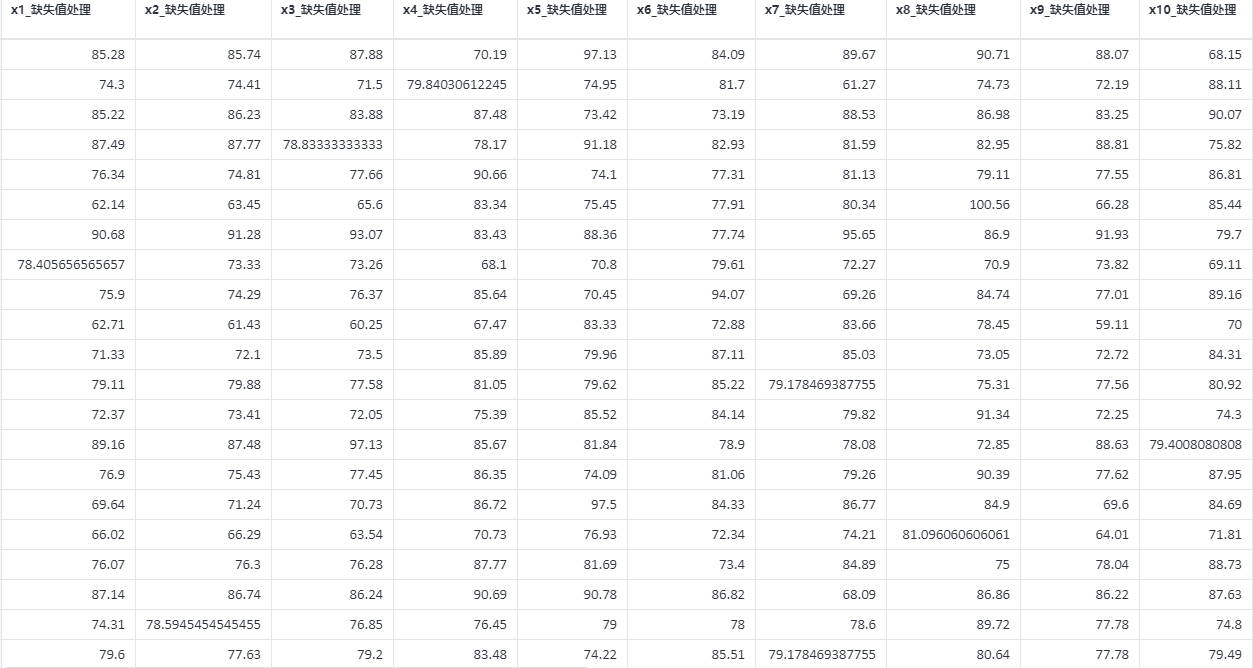
根据每一列的平均值作为填补值，来对每列的空值位置进行填补，每一列的填补操作是相互独立的，互不影响的。

# 7、注意事项

• 缺失值处理对于定类变量和定量变量要分开处理：定类变量的统计填充只存在众数填充，定量变量的统计填充存在均值、中位数、众数、三倍标准差、负三倍标准差填充。

# 8、模型理论

SPSSPRO中对于缺失值的处理方法有两大类，分别是剔除标记和填充。

# 8.1 剔除标记

剔除标记中的剔除规则是按行/列的缺失比例和缺失个数剔除，达到设定的阈值即整行或整列剔除。一般来说，如果一行数据中的缺失比例超过 50% 到 70%，就有可能考虑删除整行数据。然而，这个阈值可以根据具体的数据集特征、分析目的以及领域背景进行调整。

# 8.2 填充

# 8.2.1 统计量填充

均值填充： 计算整个特征（列）的均值，并用该均值来填补缺失值。

• 适用场景：适合处理数值型数据，特别是服从近似正态分布的数据。
• 优点：简单易行，不会改变数据的分布特性。
• 缺点：对于有极端值（异常值）存在的数据，均值容易受到影响，不适合用于非正态分布的数据。

中位数： 计算整个特征（列）的中位数，并用该中位数来填补缺失值。

• 适用场景：适合处理有偏分布和存在异常值的数值型数据。
• 优点：对于数据存在异常值或者偏态分布的情况下表现更稳健。
• 缺点：可能会对数据分布造成略微的改变，特别是在缺失值较多的情况下。

众数： 计算整个特征（列）的众数（即出现频率最高的值），并用该众数来填补缺失值。

• 适用场景：适合处理分类变量或者分类型数据的缺失值。
• 优点：简单快速，特别适合处理分类型变量的缺失。
• 缺点：可能会导致数据的偏斜，尤其是在众数出现频率较高的情况下。

三倍标准差或负三倍标准差： 计算整个特征（列）的均值$\mu$和标准差$\sigma$，然后用$\mu +3\ast \sigma$的值来填充缺失值（正三倍标准差填充）或者用$\mu -3\ast \sigma$的值来填充缺失值（负三倍标准差填充）。

• 适用场景：适合处理数值型数据，尤其是有正态分布假设的情况下。
• 优点：基于数据分布的统计特性来填充，可以保持数据的统计特性。
• 缺点：对于非正态分布或者有较多异常值的数据，效果可能不佳；另外，填充的结果可能会超出数据的实际取值范围。

# 8.2.2 规则填充

纵向用缺失值上面的值替换缺失值： 对于每个缺失值，用该值上面的非缺失值进行填充。如果上方没有非缺失值，则继续向上搜索直到找到非缺失值。

• 适用场景：适用于时间序列数据或者有序数据，缺失值可能由于某种持续性影响。
• 优点：保留了时间序列数据的顺序性或者数据的某种逻辑关系。
• 缺点：依赖于数据的顺序性，可能会引入一定的偏差或者错误填充的情况。

纵向用缺失值下面的值替换缺失值： 与上述类似，如果下方没有非缺失值，则继续向下搜索直到找到非缺失值。

若某行全为缺失值，剔除所在行： 扫描每行数据，如果发现整行都是缺失值，则将该行从数据集中删除。

固定值M填充： 将数据集中所有的缺失值替换为预先指定的固定值M。

• 适用场景：适用于处理数据集中出现的随机或无法获取的缺失值。常见的固定值可以是0、-1、999等，具体取决于数据的含义和背景知识。
• 优点：简单易行，不需要复杂的计算或推断，适用于一些较为简单的数据分析场景。
• 缺点：可能会引入数据的偏差，特别是当固定值M与实际数据的分布特征不匹配时。此外，也可能掩盖了数据中的真实模式或趋势。

# 8.2.3 插值填充

插值填充是一种更为复杂和精细的缺失值处理技术，适用于连续型数据或者有序数据。

Nearest最近点数值填充： 对于每个缺失值，找到最接近它的非缺失值，并用该非缺失值来填充缺失值。

• 适用场景：适用于数据点在空间中密集分布的情况，例如时间序列数据或者一维数据。
• 优点：简单快速，适合处理不规则间隔或分布不均匀的数据。
• 缺点：可能无法捕捉到数据中的实际趋势或模式，特别是在数据分布不均匀或者有较多异常值的情况下。

假设我们有一列数据$y$，其中第$i$个数据点$y_i$是已知的，要对第$j$个位置的缺失值$y_j$进行插值，则其数学公式可以表示为：

$$y_j=y_i\mathrm{其}\mathrm{中}i=\arg \underset{k}{min}(|k-j|)$$

这里的$\arg \underset{k}{min}(|k-j|)$表示找到离$j$最近的已知值的索引$i$。

Zero零阶插值填充： 用缺失值前一个非缺失值（向前填充）来填充缺失值。

• 适用场景：适用于处理离散型数据或者类别数据，尤其是需要保留原始数据分布的情况。
• 优点：简单易行，保留了数据的原始分布特性。
• 缺点：可能会引入数据的偏差，特别是当数据存在缺失值聚集或者缺失值分布不均匀的情况下。

Linear线性插值填充： 通过已知的非缺失值数据点，基于线性关系来估计缺失值。

• 适用场景：适用于连续型数值数据，假设数据在插值区间内呈线性关系。
• 优点：能够较好地估计线性趋势，填充后的数据平滑性较好。
• 缺点：对于非线性的数据关系表现不佳，可能导致填充值与实际值有较大偏差。

如果我们有两个已知数据点$(x_i,y_i)$和$(x_{i+1},y_{i+1})$，其中$x_i<x_j<x_{i+1}$，要对$x_j$处的缺失值$y_j$进行线性插值，其数学公式可以表示为：

$$y_j=y_i+\frac{(x_j-x_i)(y_{i+1}-y_i)}{x_{i+1}-x_i}$$

quadratic二次插值填充： 利用已知的非缺失值数据点，通过二次函数拟合来估计缺失值。

• 适用场景：适用于数据中存在二次关系或曲线关系的情况，能够更好地适应非线性数据分布。
• 优点：相较于线性插值，能够更好地逼近实际数据的曲线趋势。
• 缺点：计算复杂度较高，对于数据噪声较大或者样本量较小的情况下，可能会出现过拟合或者填充值不稳定的问题。

如果我们有三个已知数据点$(x_{i-1},y_{i-1})$,$(x_i,y_i)$和$(x_{i+1},y_{i+1})$,要对$x_j$处的缺失值$y_j$进行二次插值，其数学公式为：

$$y_j=y_i\frac{(x_j-x_{i-1})(x_j-x_{i+1})}{(x_i-x_{i-1})(x_i-x_{i+1})}+y_{i-1}\frac{(x_j-x_i)(x_j-x_{i+1})}{(x_{i-1}-x_i)(x_{i-1}-x_{i+1})}+y_{i+1}\frac{(x_j-x_i)(x_j-x_{i-1})}{(x_{i+1}-x_i)(x_{i+1}-x_{i-1})}$$

cubic三次插值填充： 利用已知的非缺失值数据点，通过三次函数拟合来估计缺失值。

• 适用场景：适用于数据中存在三次关系或曲线关系的情况，能够更准确地逼近非线性数据分布。
• 优点：能够更精确地拟合复杂的数据模式，填充后的数据平滑性和准确性较高。
• 缺点：同样的，计算复杂度较高，对于数据噪声较大或者样本量较小的情况下，需要谨慎使用以避免过拟合。

如果我们有四个已知数据点$(x_{i-1},y_{i-1})$,$(x_i,y_i)$,$(x_{i+1},y_{i+1})$,$(x_{i+1},y_{i+1})$，要对$x_j$处的缺失值$y_j$进行三次插值，其数学公式为：

$$y_i=a+b(x_j-x_i)+c(x_j-x_i{)}^2+d(x_j-x_i{)}^3$$

其中，$a$,$b$,$c$,$d$是通过这四个已知点计算得到的系数。

# 8.2.4 模型填充

模型填充方法基于已有数据构建统计模型，然后利用这些模型对缺失值进行预测和填充，适用于复杂数据模式的填充。

最小二乘填充： 通过最小化实际观测值和预测值之间的残差平方和来估计缺失值。

• 优点：简单易行，计算量较小。在数据之间存在线性关系时表现良好。
• 缺点：对数据的线性关系要求较高，对非线性关系的数据填充效果不佳。
• 适用场景：数据具有明显的线性趋势和关系。

贝叶斯填充： 利用贝叶斯统计方法处理缺失数据，通过概率分布的贝叶斯推断来预测缺失值。

• 优点：能够处理不确定性较大的数据情况，提供了缺失值的概率分布。能够利用先验信息和后验分布对数据进行更为准确的推断和填充。
• 缺点：对数据分布和模型假设要求较高。计算复杂度较高，特别是在处理大规模数据时需要考虑效率问题。
• 适用场景：数据中存在不确定性或随机性较大的情况。需要提供缺失值的概率估计。

决策树填充：

• 优点：能够处理非线性关系和复杂的数据模式。在特征选择和数据分割方面比较灵活，不需要对数据进行线性假设。
• 缺点：对数据噪声敏感，可能会导致过拟合。对参数调优和模型结构选择有一定要求。
• 适用场景：当数据中存在非线性关系或者复杂的数据模式。或需要一种能够自适应数据特征和关系的填充方法时。

k近邻填充： 通过查找最接近的$k$个样本来预测缺失值，通常使用欧氏距离或其他距离度量来确定最近邻。

• 优点：能够利用数据集中的局部信息进行填充，适用于相似度度量在数据中有意义的情况。
• 缺点：对$k$的选择比较敏感，需要进行合适的参数调优。当数据集稀疏或者维度较高时，计算复杂度可能较高。
• 适用场景：数据集中存在明显的局部相关性或者相似性。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.