季节性ARIMA模型
# 1、作用
季节性ARIMA模型能识别数据的周期性效应(包括季度、月度、年度等),进而对数据进行有效的预测。
# 2、输入输出描述
输入:1个时间序列数据定量变量
输出:未来N天的预测值
# 3、案例示例
案例:基于1949年到1960年每月航空公司的乘客数量,预测未来12个月的乘客数量。
# 4、案例数据
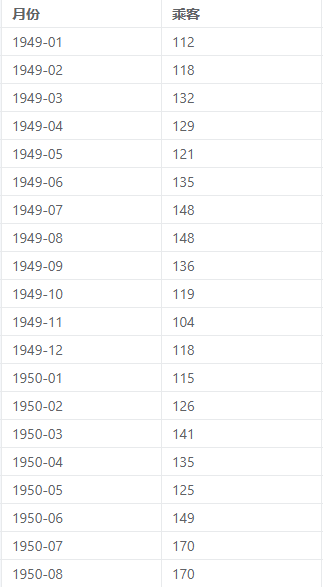
季节性ARIMA案例数据
# 5、案例操作
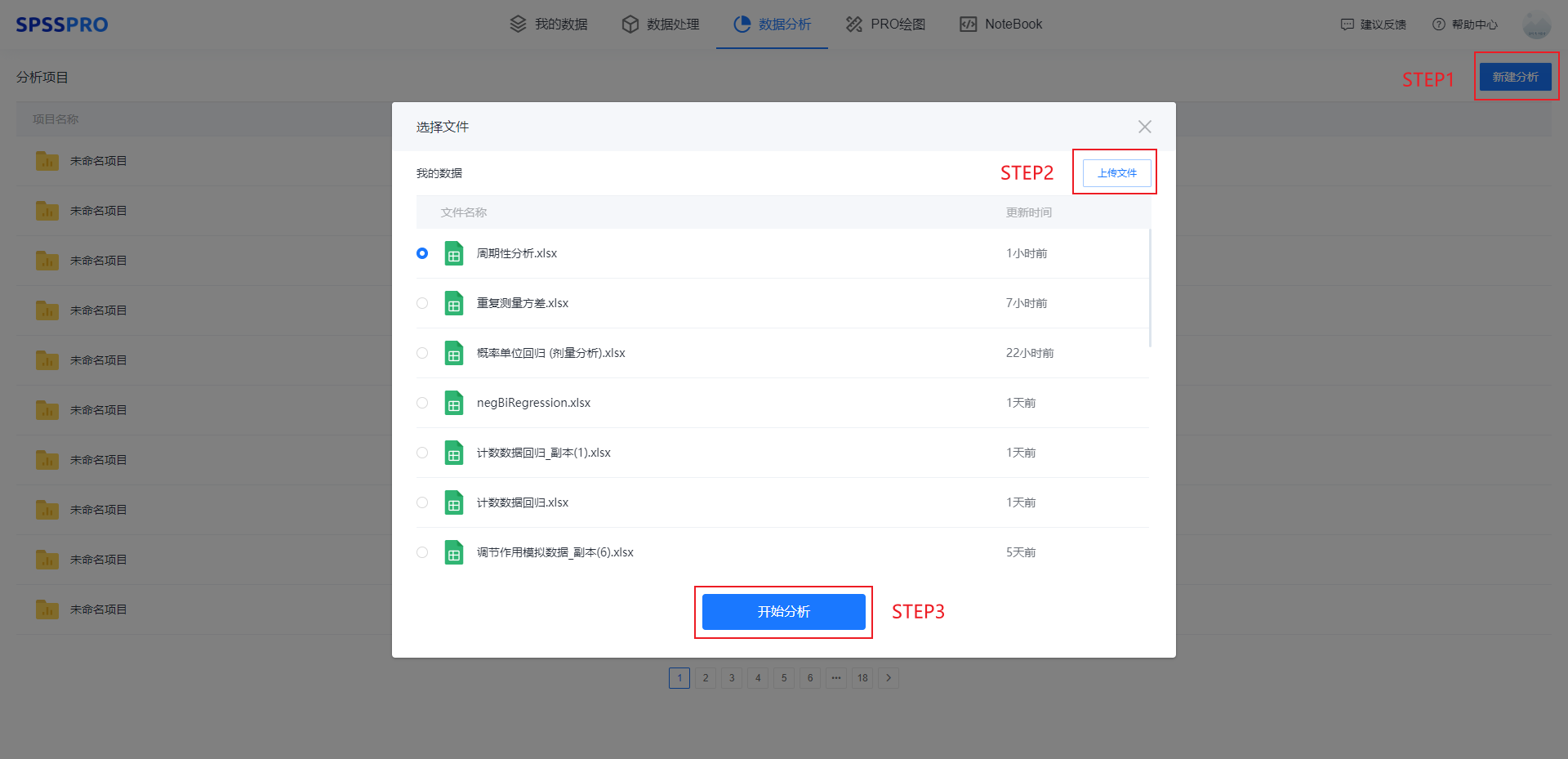
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;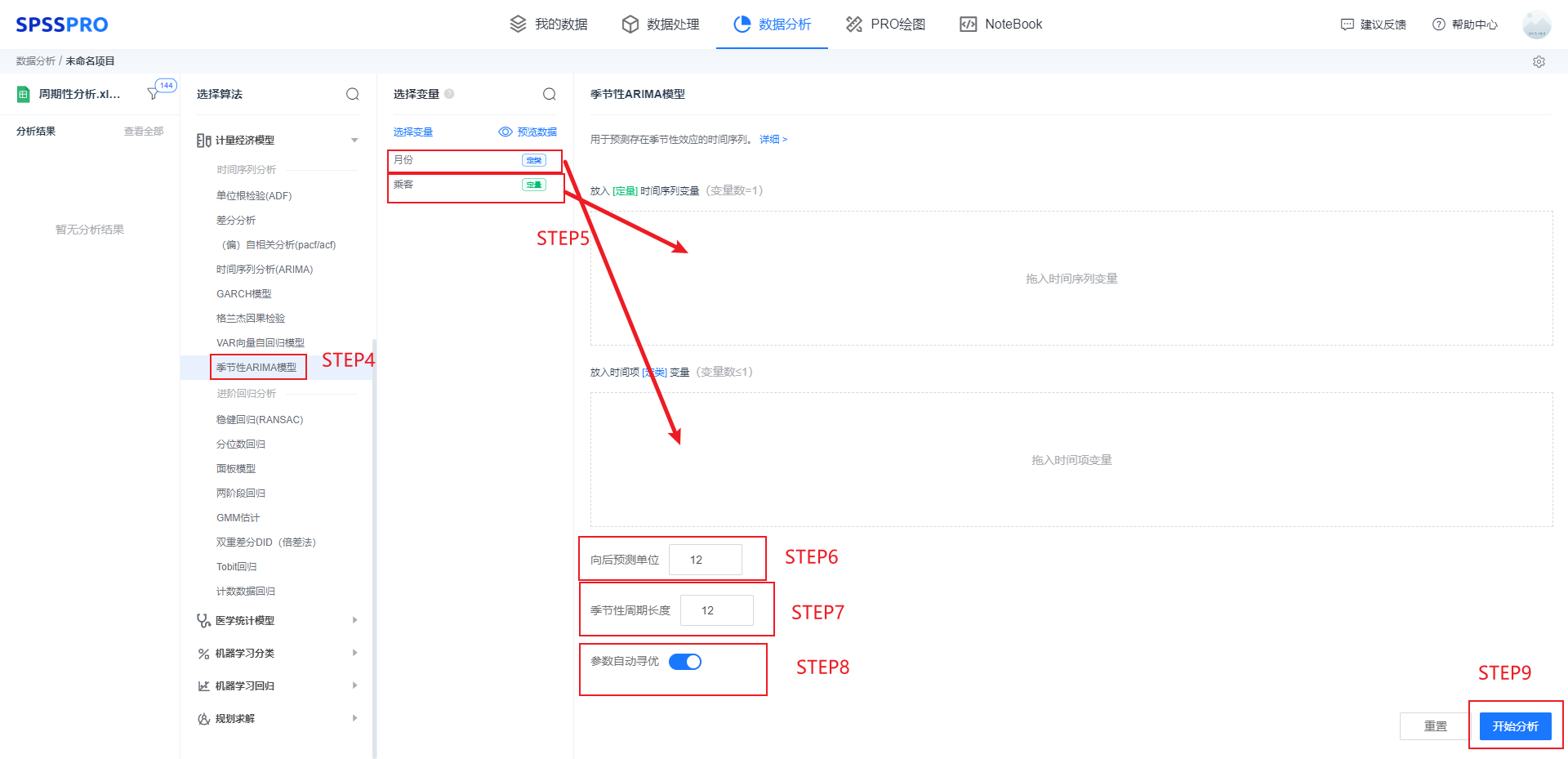
step4:选择【季节性ARIMA模型】;
step5:查看对应的数据数据格式,【季节性ARIMA模型】要求输入1个时间序列数据定量变量;
step6:选择向后预测的单位数;
step7:输入季节性周期长度(需要根据数据本身的情况来决定,如本例根据数据本身情况确定季节性周期长度为12);
step8:输入季节性ARIMA模型的参数(本例使用参数自动寻优得到结果);
step9:点击【开始分析】,完成全部操作。
# 6、输出结果分析
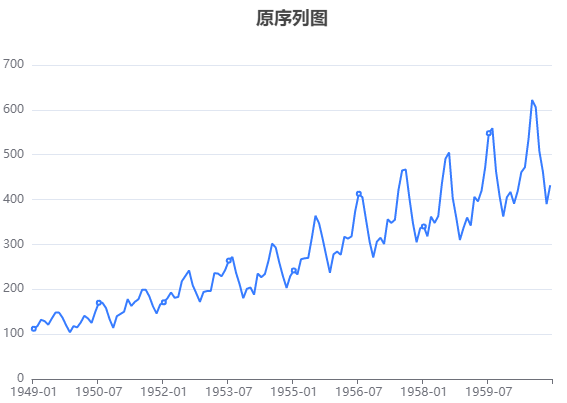
输出结果1:序列分解图

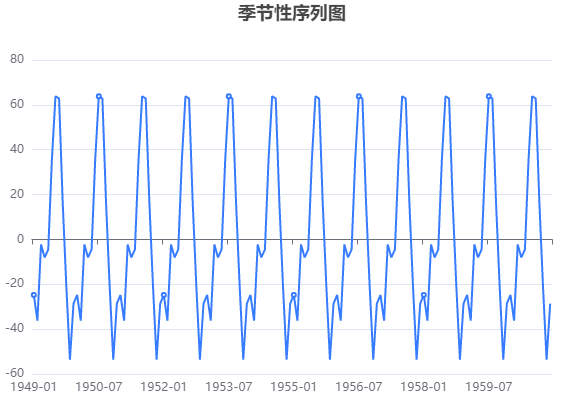
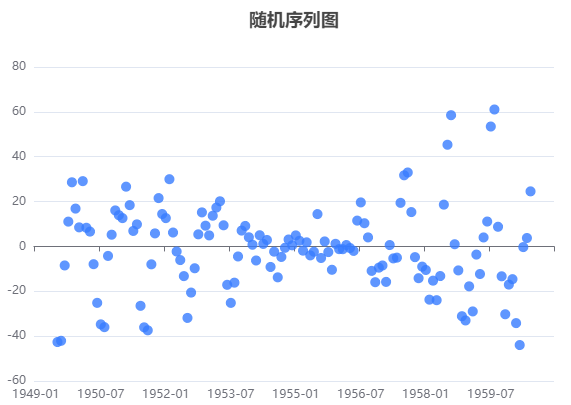
智能分析:
上图展示了原始数据分解出来的趋势数据、季节性数据、随机数据,用于初步判断序列是否存在季节性效应。
● 趋势数据:趋势显示了长时间序列数据的总体方向。趋势可以是递增(向上),递减(向下)或水平(平稳)。
● 季节性数据:季节性成分在时间,方向和幅度方面表现出重复的趋势。比如说每年夏季、冬季用电会比春季秋季多。
● 随机数据:这些是时间序列数据中的波动。
分析:
从以上的图可以看出,数据呈现递增趋势,同时看出变换周期为12的观测值有相似之处(反过来确认参数季节性周期长度为12正确)。且从图可得模型能够有效提取趋势数据,季节性数据和随机数据。
输出结果2:ADF检验表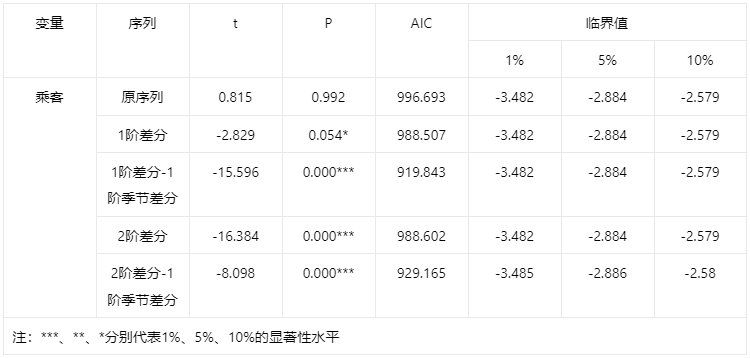
图表说明:
上表格为ADF检验的结果,包括变量、差分阶数、T检验结果、AIC值等,用于检验时间序列是否平稳。
● 该模型要求序列必须是平稳的时间序列数据。通过分析t值,分析其是否可以显著地拒绝序列不平稳的原假设。
● 若呈现显著性(P<0.05),则说明拒绝原假设,该序列为一个平稳的时间序列,反之则说明该序列为一个不平稳的时间序列。
● 临界值1%、5%、10%是不同程度拒绝原假设的统计值,ADF 检验结果同时小于1%、5%、10%即说明非常好地拒绝该假设。
● 差分阶数:本质上就是下一个数值 ,减去上一个数值,主要是消除一些波动使数据趋于平稳,非平稳序列可通过差分变换转化为平稳序列。
● AIC值:衡量统计模型拟合优良性的一种标准,数值越小越好。
● 临界值:临界值是对应于一个给定的显着性水平的固定值。
智能分析:
该序列检验的结果显示,基于变量乘客的1阶差分-1阶季节差分序列,显著性P值为0.000***,水平上呈现显著性,拒绝原假设,该序列为平稳时间序列。
分析:
为满足模型平稳,故进行ADF检验用于检验时间序列是否平稳,当原序列不能满足平稳性时会进行差分处理,但差分是对信息的提取、加工的过程,每次差分都会有信息的损失,所以差分的阶数不宜过多。
参数自动寻优时,逻辑是从原序列进行尝试,不断增加差分的阶数,直到平稳,取该阶数进行下一步分析。
输出结果3:最佳差分序列图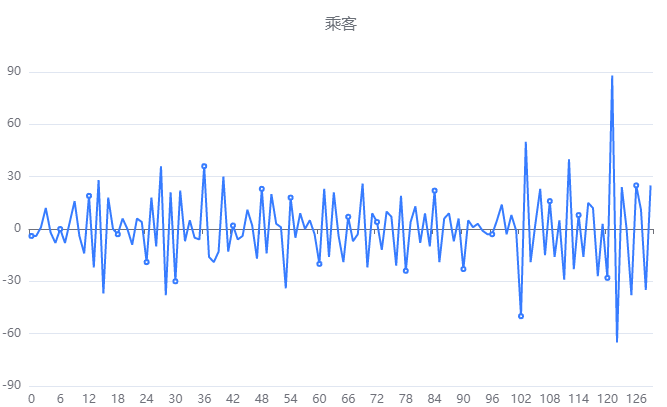
图表说明:
上图展示了原始数据1阶差分-1阶季节差分后的时序图。
分析:
展示差分后的时序图,参数自动寻优时为结果2寻得的阶数,否则为自己输入的阶数。
输出结果4:最终差分数据自相关图(ACF)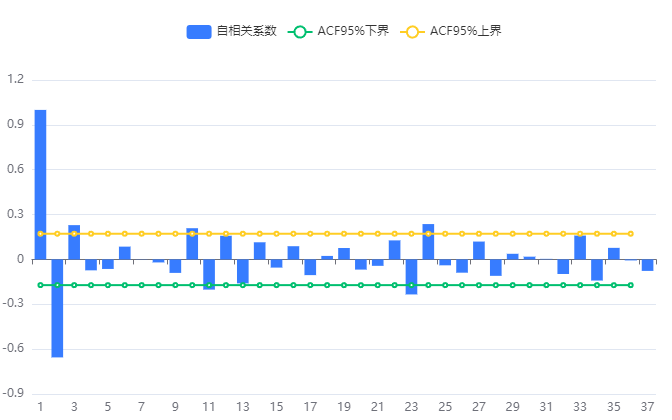
图表说明:
上图展示了自相关图(ACF),包括系数,置信上限和置信下限。可根据自相关系数和偏相关系数的拖尾、截尾情况来确定参数p、q、P、Q。
● 横轴代表延迟数目,纵轴代表自相关系数。
● 非季节性的p和q是连续时间的,即系数从1、2、3...阶进行分析。P和Q是以季节窗口(周期长度)为单位,假设当前季节窗口为4,即系数从1、5,9...阶进行分析。
分析:
可以根据原先的判断准则(见ARIMA模型帮助文档)对ACF拖尾截尾情况进行进阶数判断,但是需要对连续时间和季节窗口进行不同的分析。
输出结果5:最终差分数据偏自相关图(PACF)
图表说明:
上图展示了偏自相关图(PACF),包括系数,置信上限和置信下限。可根据自相关系数和偏相关系数的拖尾、截尾情况来确定参数p、q、P、Q。
● 横轴代表延迟数目,纵轴代表偏自相关系数。
● 非季节性的p和q是连续时间的,即系数从1、2、3...阶进行分析。P和Q是以季节窗口(周期长度)为单位,假设当前季节窗口为4,即系数从1、5,9...阶进行分析。
分析:
可以根据原先的判断准则(见ARIMA模型帮助文档)对PACF拖尾截尾情况进行进阶数判断,但是需要对连续时间和季节窗口进行不同的分析。
输出结果6:模型评价表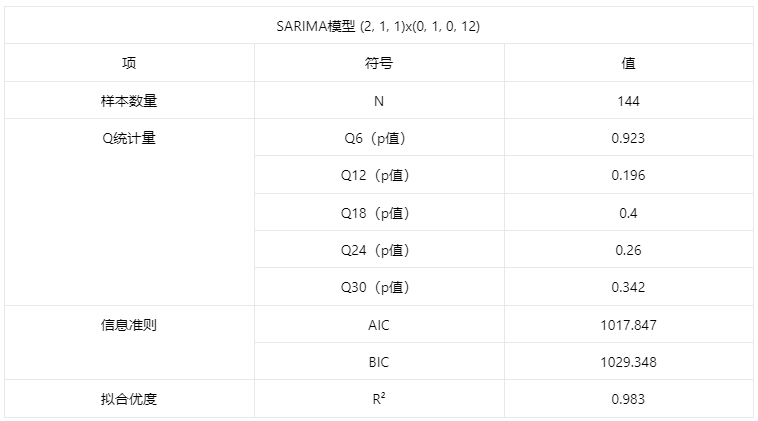
图表说明:
上表格展示本次模型检验结果,包括样本数、残差Q统计量、信息准则模型以及拟合优度。
● 季节性ARIMA模型要求模型的残差不存在自相关性,即模型残差为白噪声,查看模型检验表,根据Q统计量的P值(P值大于0.1为白噪声)对模型白噪声进行检验。
● 根据信息准则AIC和BIC值用于多次分析模型对比(越低越好)。
● R²代表时间序列的拟合程度,越接近1效果越好。
智能分析:
系统自动寻找最优参数,模型结果为SARIMAX(2, 1, 1)×(0, 1, 0, 12)。基于变量乘客,从残差Q统计量结果分析可以得到:Q6在水平上不呈现显著性,不能拒绝模型的残差为白噪声序列的假设,模型基本满足要求;模型的拟合优度R²为0.983,模型表现优秀。
输出结果7:模型参数表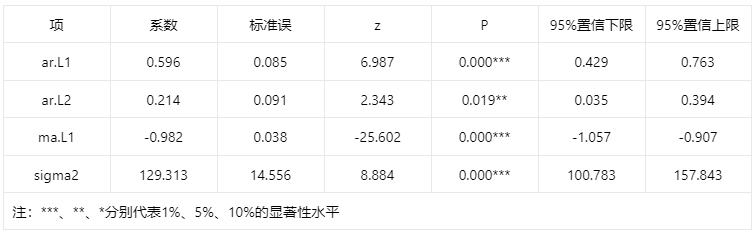
图表说明:
上表格展示本次模型参数结果,包括模型的系数、标准差,t统计量结果等,用于分析模型公式。
输出结果8:时间序列图
图表说明:
上图表示了该时间序列模型的原始数据图、模型拟合值、模型预测值。
分析:
由图可得,拟合效果优秀,模型可以用于进一步预测。
输出结果9:时间序列预测表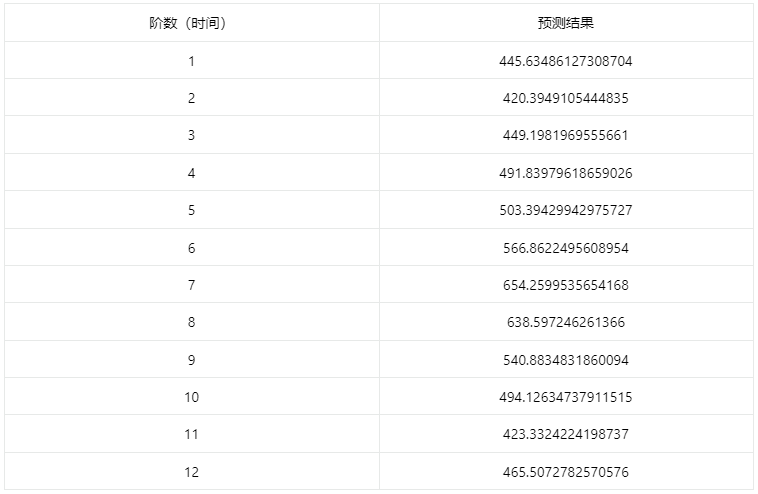
图表说明:
上表显示了时间序列模型最近12期数据预测情况。
# 7、注意事项
- 在关闭参数自动寻优,自行定参数时,参数(p/d/q/P/D/Q)均不宜过大,差分阶层(d/D)为0/1一般就可满足需求。
- 系统默认采用AIC准则对参数(p/d/q/P/D/Q)进行寻优定阶,采用ADF检验+差分分析选择最优的差分阶层(d/D)。
# 8、模型理论
# 季节ARIMA模型是什么
季节ARIMA模型(SARIMA)是表述最全面的时间序列预测模型之一,其他的模型都可以由它简化变型后得到。其建模思想是,将预测对象随时间推移而形成的数据序列看作一个随机序列,时间序列是一组依赖时间*的随机变量,构成该时间序列的单个序列值虽然具有不确定性,但整个序列的变化却是有一定的规律性,可以用数学模型近似描述。这组随机变量所具有的依存关系或自相关性表征了预测对象发展的延续性,而一旦这种自相关性被相应的数学模型描述出来,就可以从时间序列的过去值预测其未来值,通过SARIMA模型可以消除趋势性和季节性,转化为平稳时间序列进行建模。
# 季节ARIMA模型原理
设季节性序列(月度、季度、周度等序列都包括其中)的变化周期为S(季节性周期长度),即时间间隔为S的观测值有相似之处。首先用季节差分的方法消除周期性变化。季节差分算子定义为:
若季节性时间序列用表示,则一次季节差分表示为:
对于非平稳季节性时间序列,有时需要进行D次季节差分之后才能转换为平稳的序列。在此基础上可以建立关于周期为S的P阶自回归Q阶移动平均季节时间序列模型:
对于上述模型,相当于假定
当
其中
的一阶(非季节)差分次数。由上式的:
代入上式进入移动平均季节时间序列模型可得:
其中下标P,Q,p,q分别表示季节与非季节自回归、移动平均算子的最大滞后阶数,d,D分别表示非季节和季节性差分次数。上式称作
对于乘积季节模型的季节阶数,即周期长度S的识别可以通过自相关和偏相关图得到,如果相关图和偏相关图不是呈线性衰减趋势,而是变化周期的整数倍时点上出现绝对值相当大的峰值并呈现震荡式变化,就可以认为该时间序列可以用SARIMA模型描述。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 郝军章, 崔玉杰, 韩江雪. 基于SARIMA模型在我国铁路客运量中的预测[J]. 数学的实践与认识, 2015(18):10.
