# 差分分析

# 1、作用

差分，本质上就是下一个数值减去上一个数值，主要是消除一些波动使数据趋于平稳，非平稳序列可通过差分变换转化为平稳序列。

# 2、输入输出描述

输入:１个时间序列数据定量变量
输出:经过指定阶数差分后的序列图
​

# 3、案例示例

案例:基于某杂志 1995-2019 年的印刷量数据，对其分别进行一阶差分和二阶差分。

# 4、案例数据

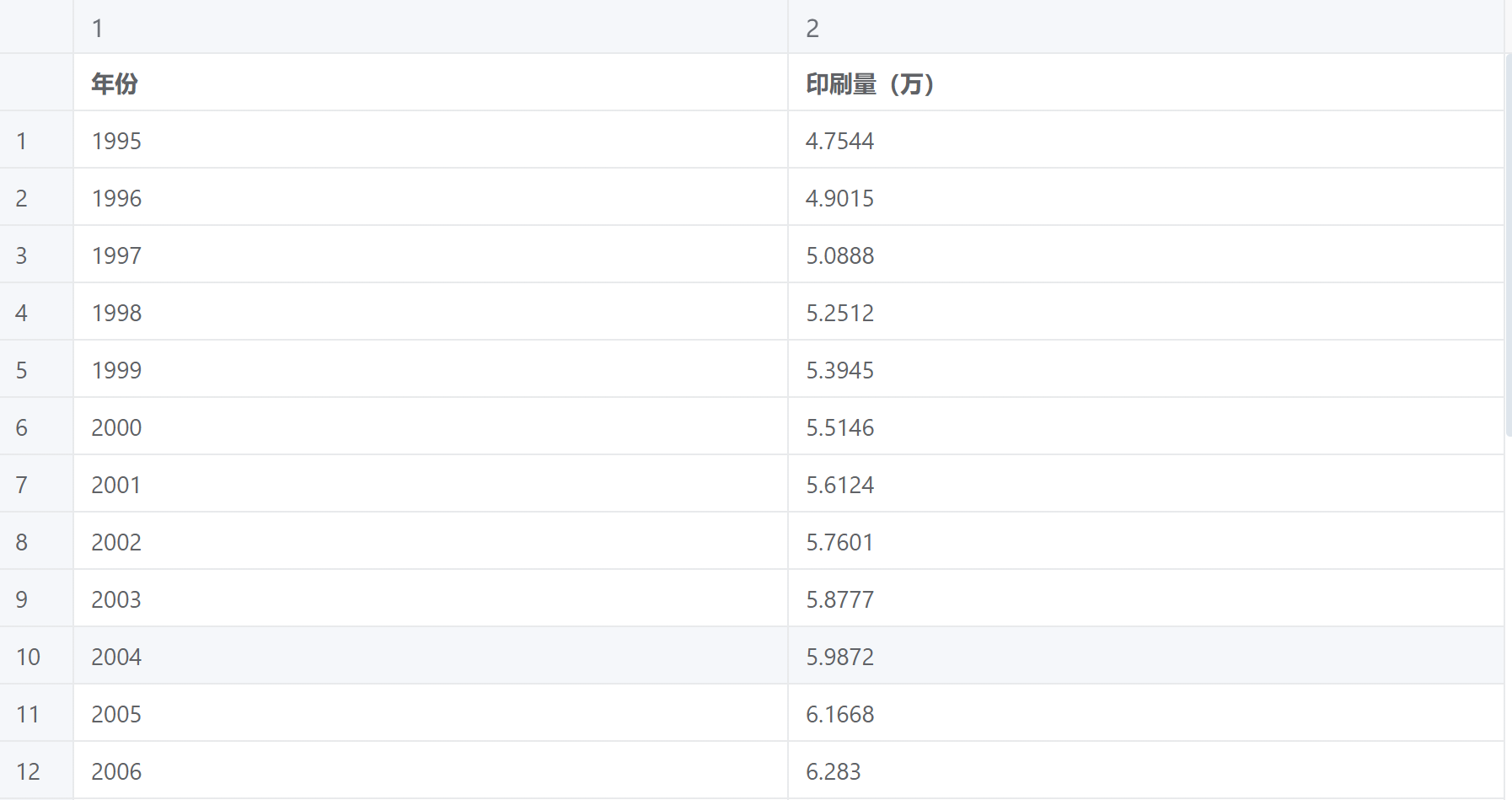
差分分析案例数据

# 5、案例操作

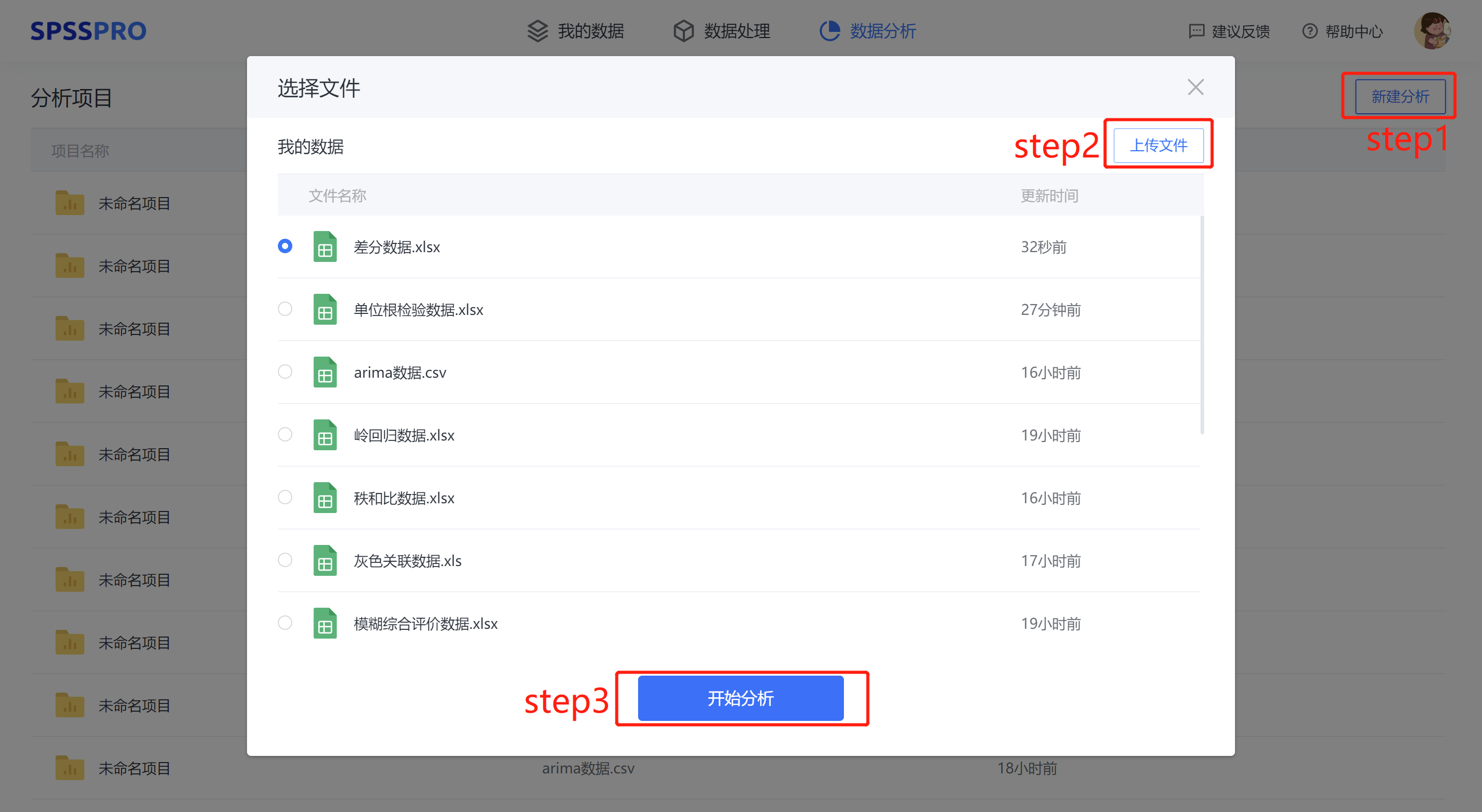
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；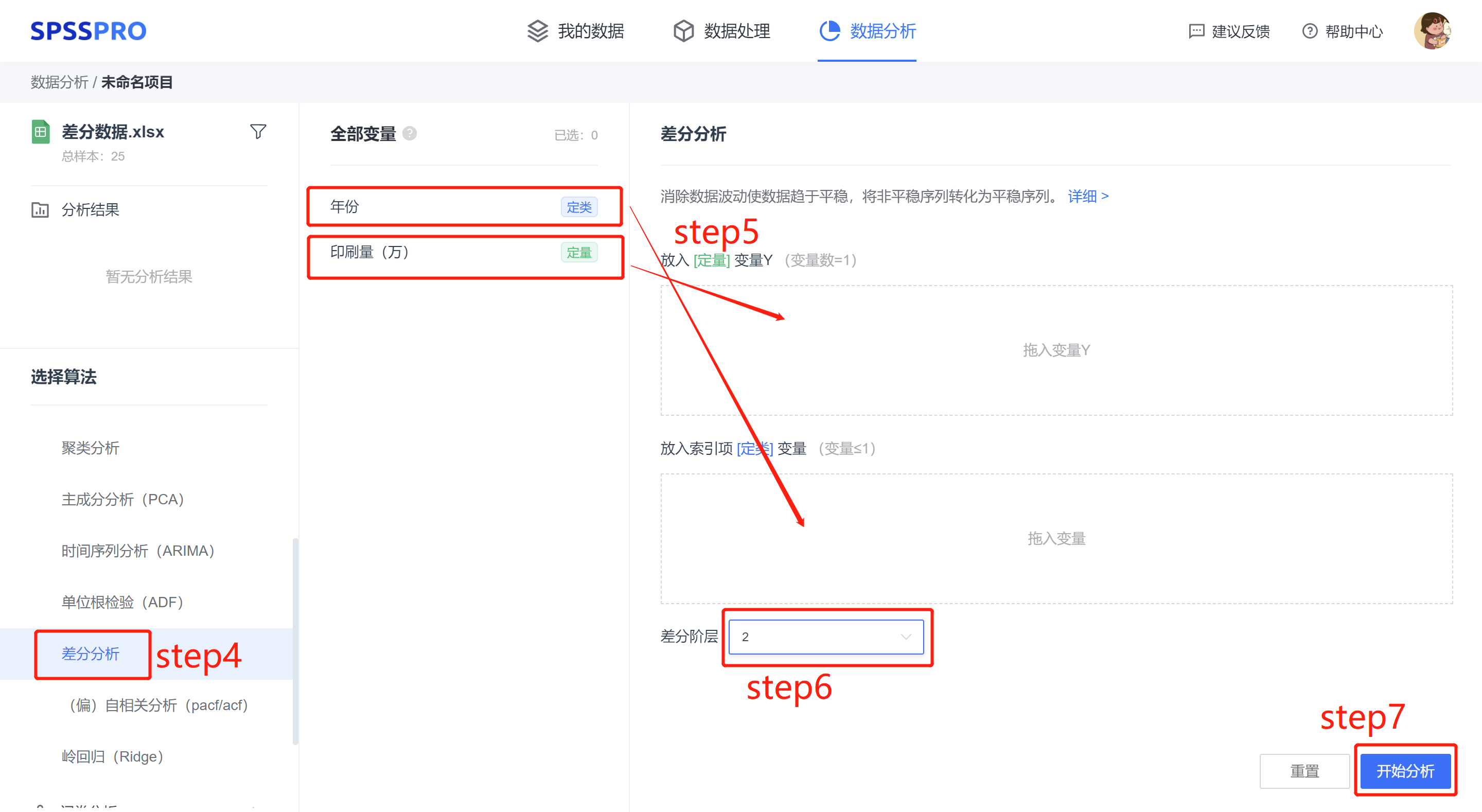

step4：选择【差分分析】；
step5：查看对应的数据数据格式，【差分分析】要求输入１个时间序列数据定量变量。
step6：设置差分阶数（注意：选定差分阶级，一般来说超过二阶差分在统计学上没有参考意义）
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：原始序列图

图表说明:上图展示了未进行差分的原始图。其中 X 轴代表时间项（年份），Y 轴代表数值（杂志印刷量）。主观来看，原序列图有个递增的趋势，是非平稳序列。我们需要通过差分将非平稳原序列图转换成平稳序列。
​

输出结果 2：一阶差分图

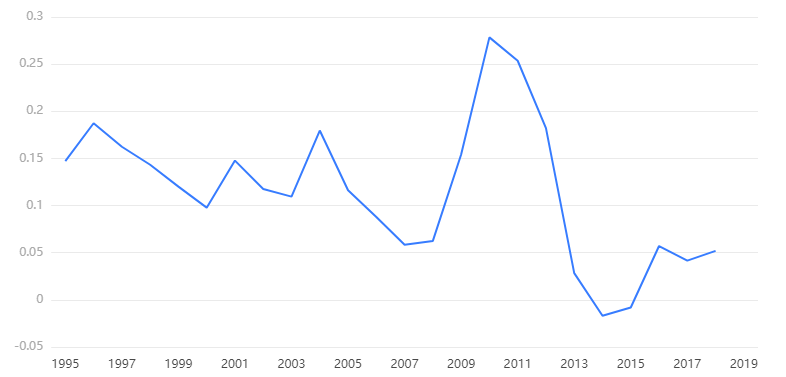
图表说明:上图展示了进行一阶差分的结果图。当时间间距相等时，用下一个数值，减去上一个数值 ，得到一阶差分。主观来看，一阶差分序列在数值 1.5 上下波动，没有明显的递增递减趋势，初步判断一阶差分序列为平稳序列。为了避免人为主观性判断，可以通过 ADF 单位根检验去判断一阶差分序列是否平稳。
​

输出结果 3：二阶差分图

图表说明:上图展示了进行二阶差分的结果图。做两次相同的动作，即再在一阶差分的基础上用后一个数值再减上一个数值一次，就叫“二阶差分”。对于二阶差分序列的平稳性检验，可以通过 ADF 单位根检验去判断二阶差分序列是否平稳。

# 7、注意事项

• 一般可以通过 ADF 检验来量化评估数值差分后，是否呈现稳定性

# 8、模型理论

差分又名差分函数或差分运算，差分的结果反映了离散量之间的一种变化，是研究离散数学的一种工具。
设函数 ，式中只对 在非负整数值上有定义，在自变量 x 依次取遍非负整数，即 时，相应的函数值为。简记为

定义 1 当自变量从变到 时，函数 的改变量

称为函数 在点 的一阶差分，通常记作

定义 2 当自变量从变到 时，一阶差分的差分

称为函数 的二阶差分，记作 ，即

同样，二阶差分的差分称为三阶差分，记为 ，即

依此类推，可得函数的 n 阶差分为

​

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 姚志鹏，何丹，崔唯．微积分：华中师范大学出版社，2015.05