GARCH模型

# 1、作用

GARCH 模型能模拟时间序列变量的波动性的变化，解决了传统的计量经济学对时间序列变量的第二个假设（方差恒定）所引起的问题。

# 2、输入输出描述

输入：１个时间序列定量变量。
输出：GARCH 模型的拟合情况及计算的条件方差。

# 3、案例示例

案例：对某股票的收益率使用 GARCH 模型对其波动状况进行研究。

# 4、案例数据

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；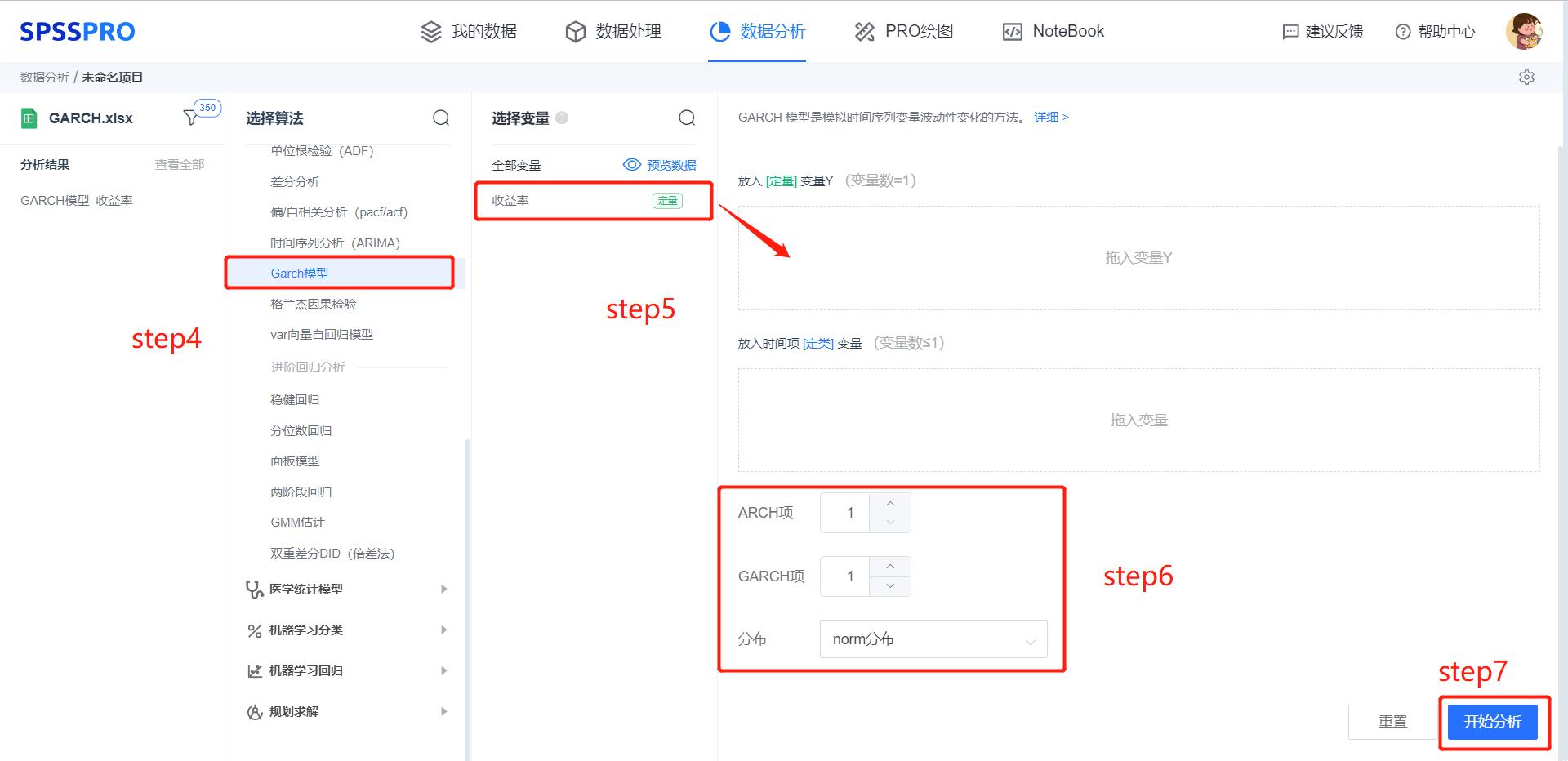

step4：选择【GARCH 模型】；
step5：查看对应的数据数据格式，【GARCH 模型】要求特征序列为１个时间序列定量变量。
step6：选择 GARCH 模型的参数和序列的假设分布。
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：平稳性检验

图表说明：该序列检验的结果显示，基于变量收益率，显著性 p 值为 0.000***，水平上呈现显著性，拒绝原假设，该序列为平稳的时间序列。

输出结果 2：ARCH 效应检验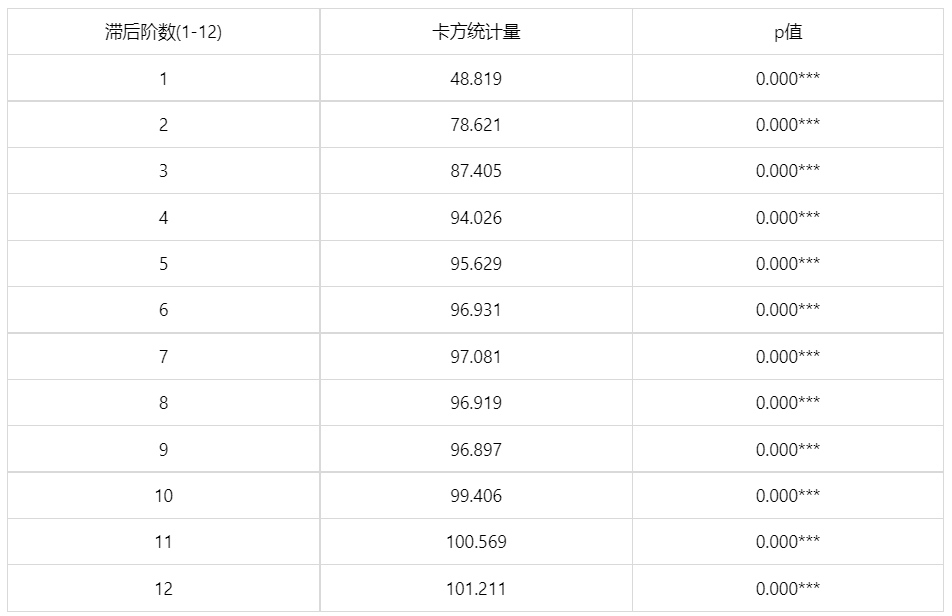

图表说明：上表展示了 ARCH-LM 拉格朗日乘子检验结果（ spsspro 只取滞后 1-12 阶的 ARCH 检验）。

• 若是只有少量滞后阶数的 p 值小于显著性水平 0.05 时，说明存在短期自相关，则可以建立 ARCH 模型。
• 若是较多滞后阶数的 p 值小于显著性水平 0.05 时，说明存在长期自相关，则可以建立 GARCH 模型。若是存在长期自相关，一般建立 GARCH(1,1) 足以，因为 GARCH 模型的实质是在 ARCH 上增加了异方差函数 q 阶自相关而形成，即相当于 ARCH(q) 的 q 是无限值。 由表格可知，较多滞后阶数的 p 值小于显著性水平 0.05 ，说明存在长期自相关，直接建立 GARCH(1,1)-norm 模型。

输出结果 3：模型参数估计结果表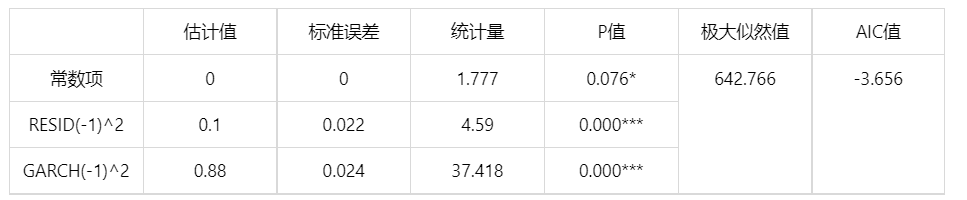

图表说明：上表展示了 GARCH 模型的参数估计结果表，用于检验模型拟合情况。稳定的 GARCH 模型需要满足：RESID 项的参数值和 GARCH 项的参数值要求都大于零；RESID 项（也就是 ARCH 项）和 GARCH 项的所有参数加和要求小于 1。所以，建立的 GARCH(1,1)-norm 模型是稳定的。

输出结果 4：标准残差纯随机性检验

图表说明：上表展示了 GARCH 模型标准残差的纯随机性检验结果，用于检验 GARCH 模型的有效性。
若有较多滞后阶数的 p 值大于等于显著性水平 0.05 时，标准残差满足随机性，说明 GARCH 很好地提取了序列的波动情况，GARCH 模型是有效的。

输出结果 5：波动率图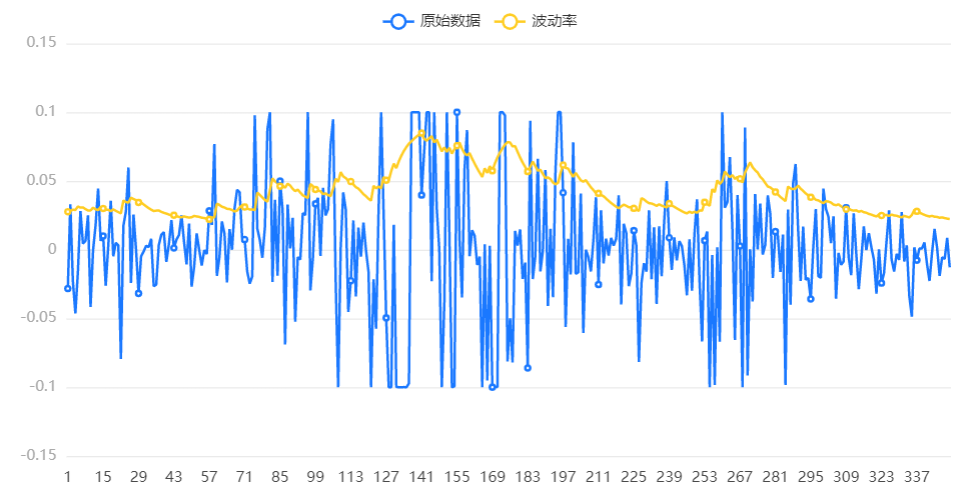

图表说明：上图展示了原序列的条件方差图，直观展现了 GARCH 模型拟合原序列波动特征的情况。

# 7、注意事项

• 若是存在长期自相关，一般建立 GARCH(1,1) 足以，因为 GARCH 模型的实质是在 ARCH 上增加了异方差函数 q 阶自相关而形成，即相当于 ARCH(q) 的 q 是无限值。

# 8、模型理论

ARCH 模型的基本思想是指在以前信息集下，某一时刻一个噪声的发生是服从正态分布。该正态分布的均值为零，方差是一个随时间变化的量(即为条件异方差)。并且这个随时间变化的方差是过去有限项噪声值平方的线性组合(即为自回归)。这样就构成了自回归条件异方差模型。

ARCH 模型的实质是使用残差平方序列的 q 阶移动平移拟合当期异方差函数值，由于移动平均模型具有自相关系数 q 阶截尾性，所以 ARCH 模型实际上只适用于异方差函数短期自相关系数。
但是在实践中，有些残差序列的异方差函数是具有长期自关性，这时使用 ARCH 模型拟合异方差函数，将会产生很高的移动平均阶数，增加参数估计的难度并最终影响 ARCH 模型的拟合精度。
为了修正个问题，提出了广义自回归条件异方差模型， 这个模型简记为 GARCH（p,q），公式为

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Bollerslev T . Generalized autoregressive conditional heteroskedasticity[J]. Eeri Research Paper, 1986, 31(3):307-327.