PP图-QQ图

操作视频

# 1、作用

P-P 图/Q-Q 图的用途一致，是用于检验数据与某一特定分布是否相似，如果被检验的数据符合所指定的分布，则代表样本数据的点应当基本在代表理论分布的（P-P 图/Q-Q 图）线上。二者的区别是 P-P 图比较的是真实的数据和待检验分布的累计概率，而 Q-Q 图比较的是真实数据和待检验分布的分位点数。

# 2、输入输出描述

输入：一项定量变量。
输出：真实数据是否基本在代表理论分布的（PP 图/QQ 图）线上。

可支持的检验：正态分布、t 分布、均匀分布、拉普拉斯分布、Logistic 分布、帕累托分布、威布尔分布、Beta 分布、卡方分布、Gamma 分布、指数分布

# 3、案例示例

案例：现有一数据，想要检验它是否服从正态分布。

# 4、案例数据

P-P/Q-Q图案例数据

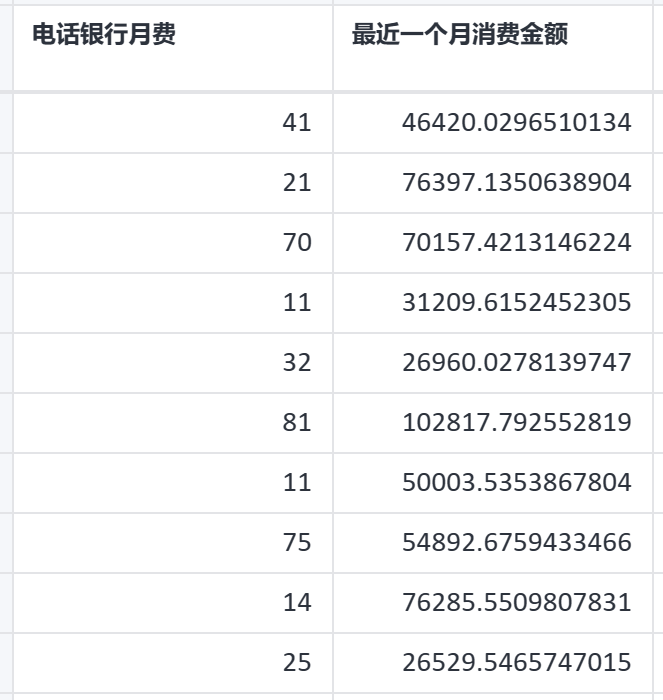
# 5、案例操作

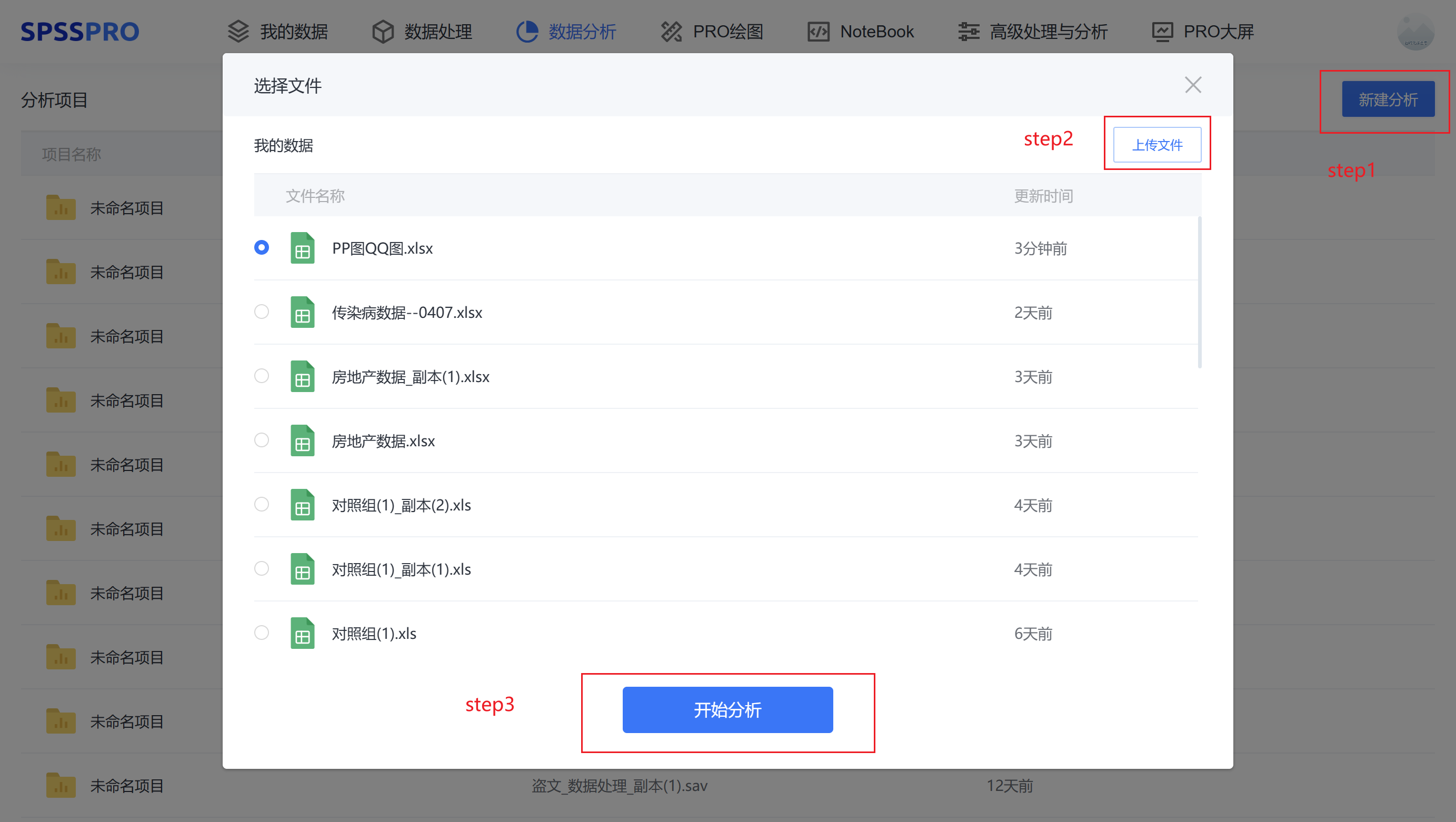
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；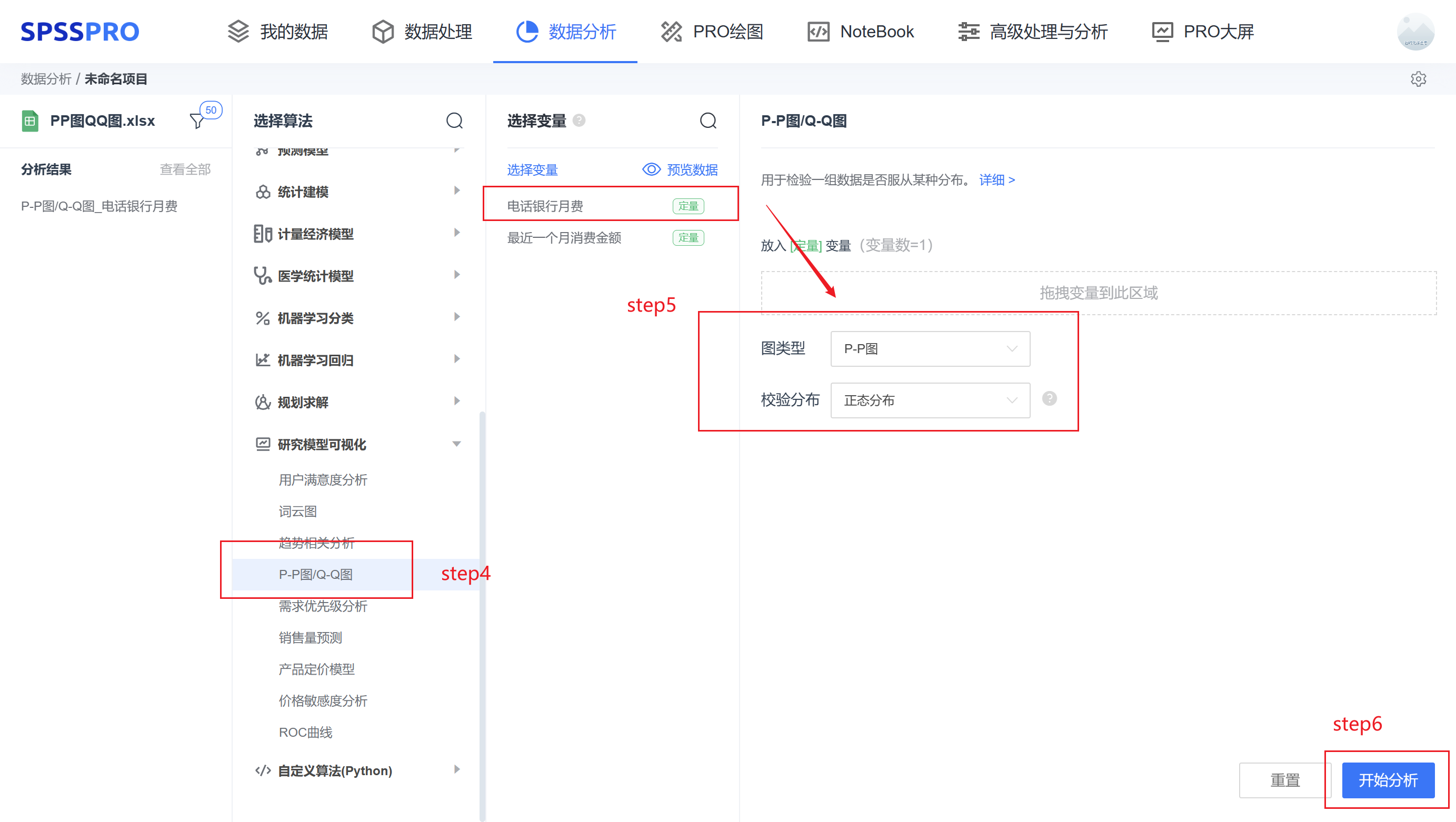

step4：选择【产品定价模型】；
step5：查看对应的数据数据格式，按要求拖入数据。
step6：点击【开始分析】。

# 6、输出结果分析

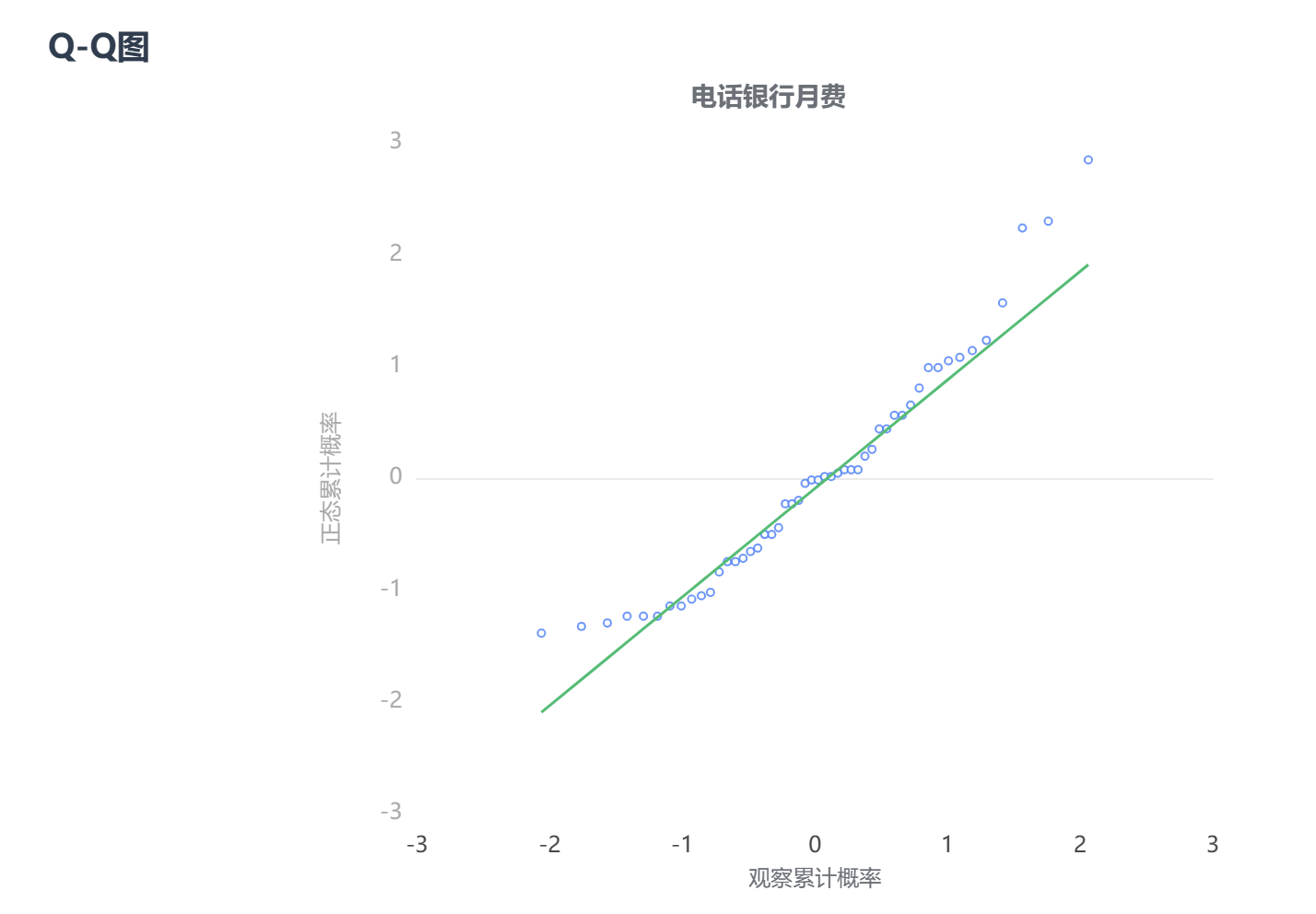
图表说明：由以上的 PP 图和 QQ 图，真实数据是否基本在代表理论分布的（PP 图/QQ 图）线上，说明该数据”电话银行月费“这个变量的数据分布是服从正态分布的。

# 7、注意事项

由于 P-P 图和 Q-Q 图的用途完全相同，只是检验方法存在差异。要利用 QQ 图鉴别样本数据是否近似于正态分布，只需看 QQ 图上的点是否近似地在一条直线附近，而且该直线的斜率为标准差，截距为均值。

# 8、模型理论

P-P 图和 Q-Q 图是两种用于检验数据分布是否符合某种理论分布的方法:
(1)P-P 图（Probability-Probability plot）：P-P 图是一种以经验分布函数为基础的图形方法。在 P-P 图中，横轴为理论分位数，纵轴为样本分位数。如果数据符合所选理论分布，那么数据点将沿着一条直线分布，直线的斜率和截距反映了数据的分布参数。P-P 图可以用于检验数据分布是否符合正态分布、指数分布等理论分布。
(2)Q-Q 图（Quantile-Quantile plot）：Q-Q 图是一种比较两种分布间的分位数之间的关系的图形方法。在 Q-Q 图中，横轴为理论分位数，纵轴为样本分位数。如果数据符合所选理论分布，那么数据点将沿着一条直线分布，直线的斜率和截距反映了数据的分布参数。Q-Q 图可以用于检验数据分布是否符合正态分布、指数分布等理论分布。

# 9、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.

建议反馈