配对样本Wilcoxon符号秩检验

# 1、作用

配对样本 Wilcoxon 符号秩检验用于比较配对的连续变量 X1 与连续变量 X2 之间的差异情况，同时配对变量差值不呈现正态性分布。
​

# 2、输入输出描述

输入：样本数相同，且差值不呈现正态分布的两个定量变量。
输出：这两个定量变量是否存在差异性。
​

# 3、案例示例

示例：检验某医院 300 个病人注射某药剂前后血压是否一致（差值非正态分布）。
​

# 4、案例数据

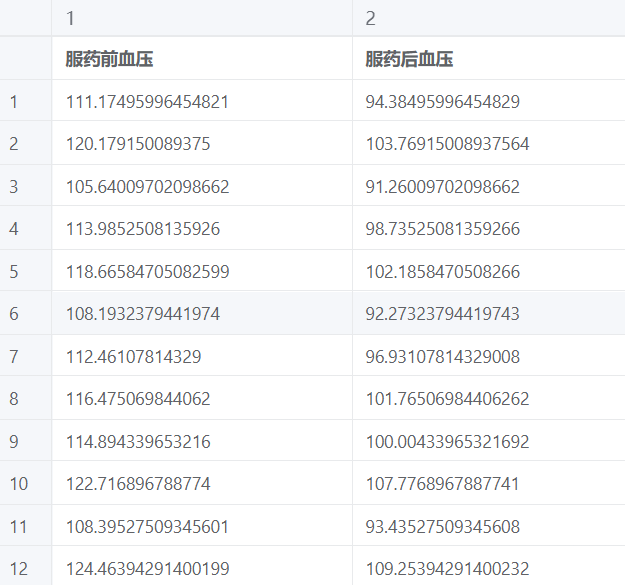
配对样本 Wilcoxon 符号秩检验

# 5、案例操作

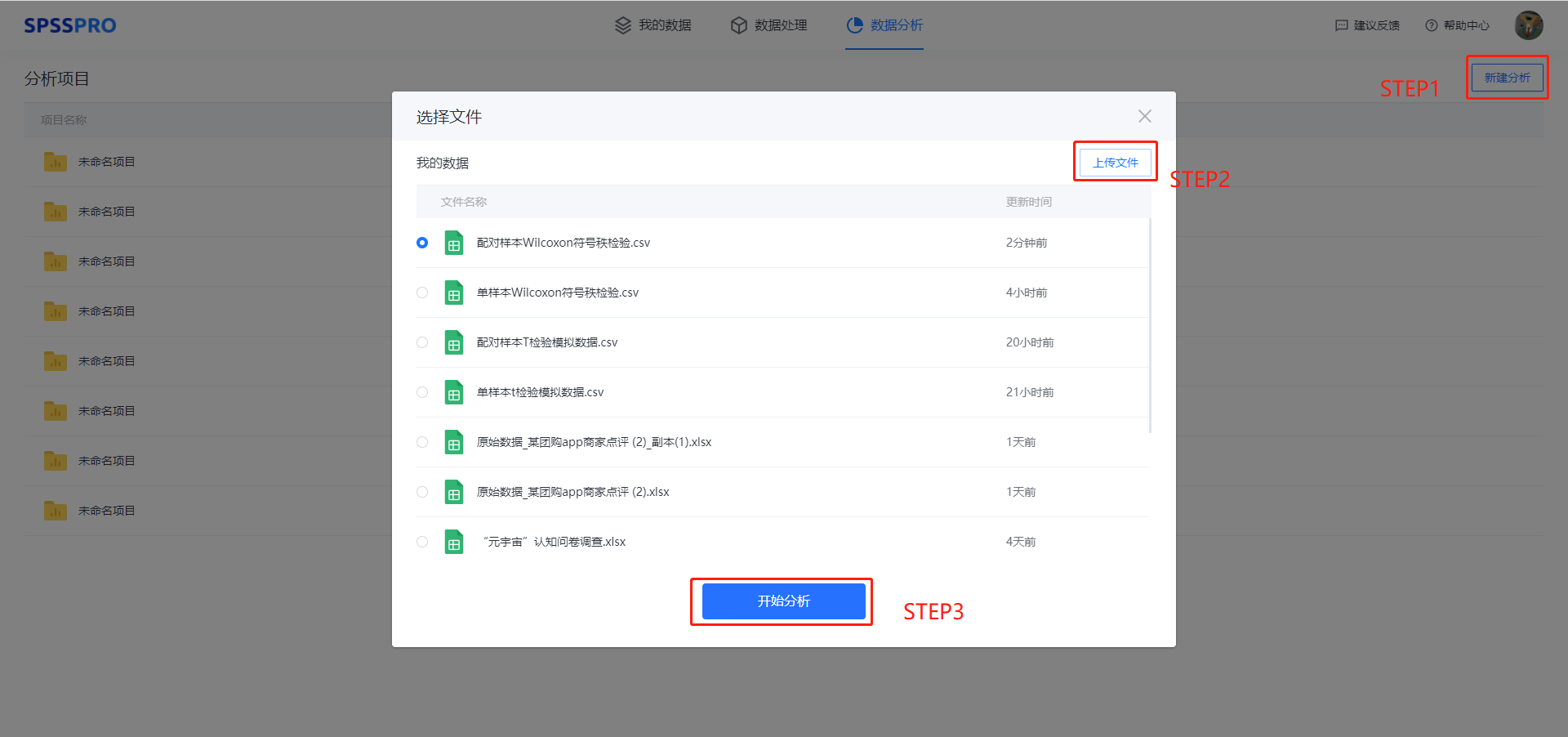
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；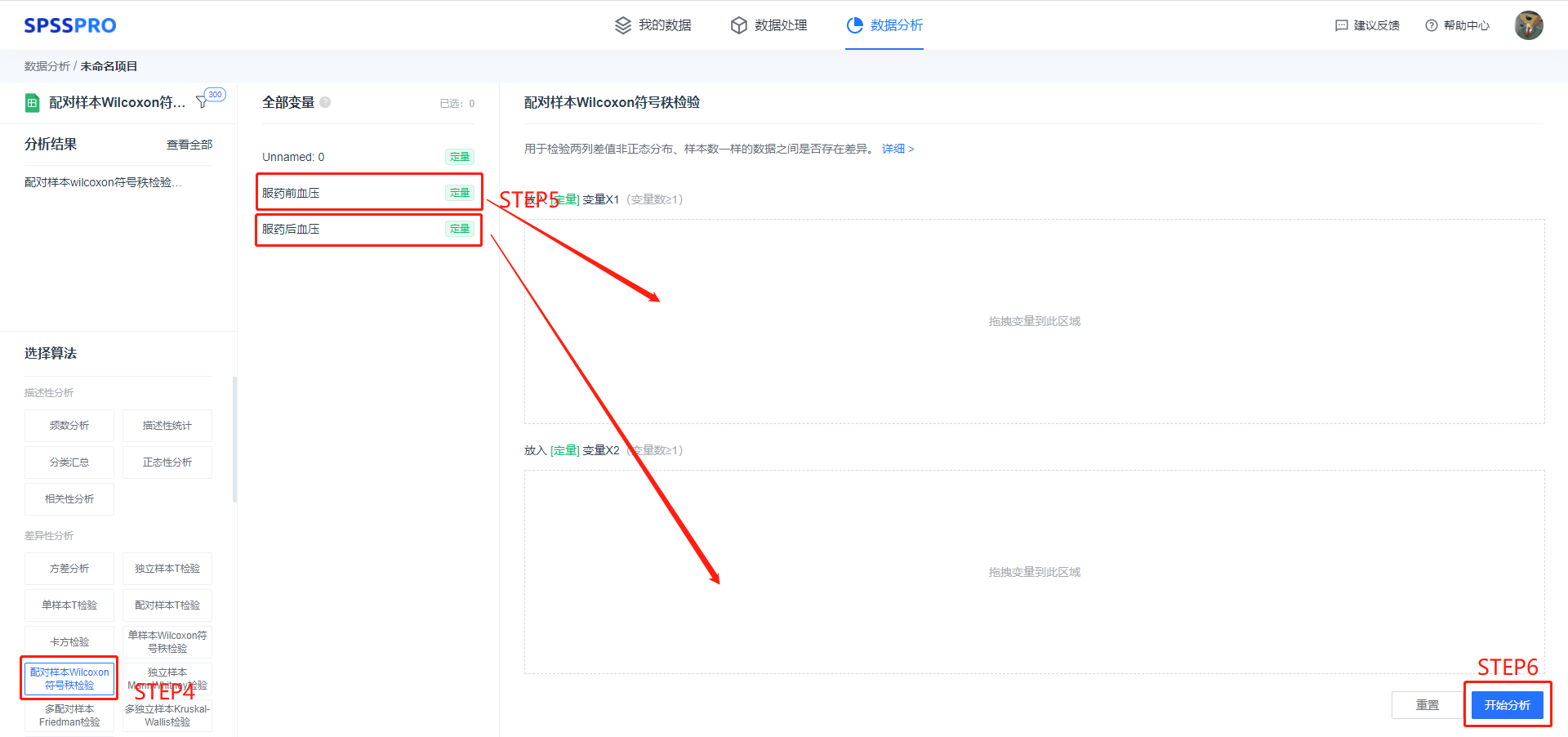

step4：选择【配对样本 Wilcoxon 符号秩检验】；
step5：查看对应的数据数据格式，【配对样本 Wilcoxon 符号秩检验】要求输入数据为定量变量，且至少有一项；
step6：点击【开始分析】，完成全部操作。
​

# 6、输出结果分析

输出结果 1：正态性检验结果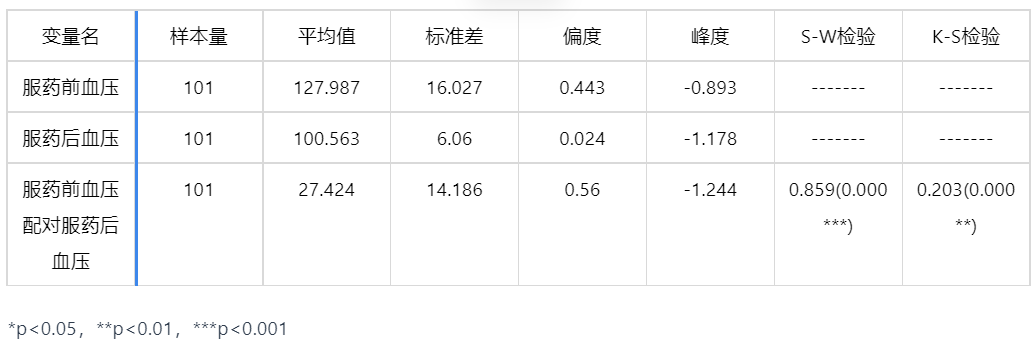

图表说明：
因为服药前血压配对服药后血压的差值样本数量 N≥5000，故采用 K-S 检验检验其正态性，显著性 P 值为 0.000，水平上不呈现显著性，不能拒绝原假设，因此数据不满足正态分布，故进行配对样本 Wilcoxon 符号秩检验。若满足正态分布则进行配对样本 t 检验。

输出结果 2：正态性检验直方图

图表说明：上图展示了定量变量服药前血压、服药后血压的差值数据正态性检验的结果：
由图可得，服药前血压、服药后血压的差值分布明显非正态分布，故进行 Wilcoxon 符号秩检验。
​

输出结果 3：配对样本 Wilcoxon 符号秩检验

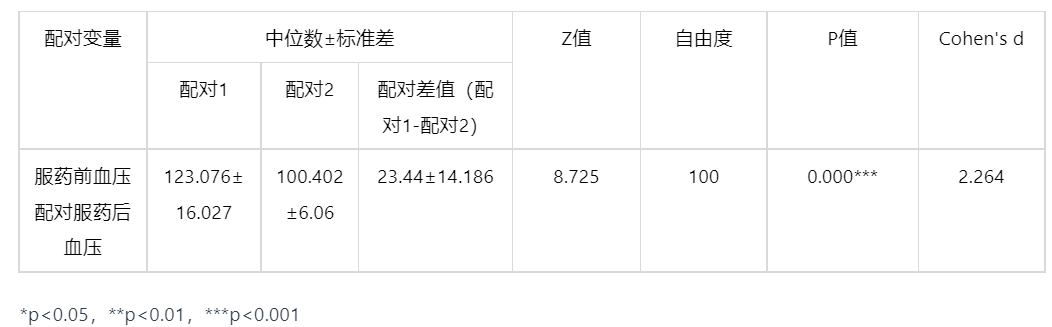
图表说明：配对样本wilcoxon检验的结果显示，基于字段服药前血压配对服药后血压的差值，显著性P值为0.000，水平上呈现显著性，拒绝原假设，因此服药前血压配对服药后血压之间存在显著性差异。 其差异幅度Cohen's d值为：2.264，差异幅度非常大。

# 7、注意事项

• 当需要比较配对样本变量差值的差异情况时，如果发现数据呈非正态分布并无法转换为正态分布时，选择配对样本样本 Wilcoxon 符号秩检验，否则使用配对样本 t 检验。
• 各差异性分析模型的使用场景如下总结：

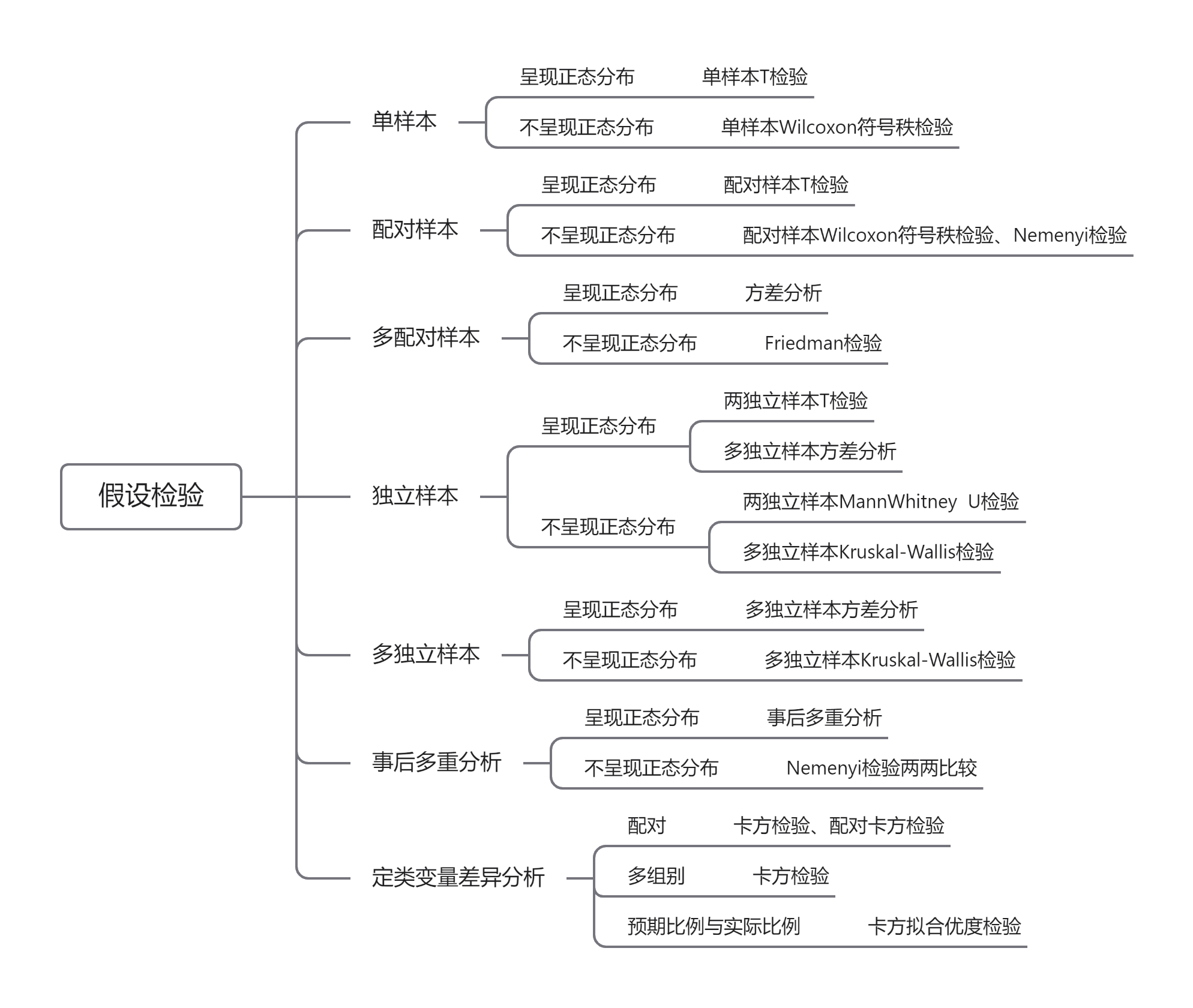
# 8、模型理论

Wilcoxon 符号秩检验，它把观测值和零假设的中心位置之差的绝对值的秩分别按照不同的符号相加作为其检验统计量。它适用于 T 检验中的成对比较，但并不要求成对数据之差 di 服从正态分布，只要求对称分布即可。检验成对观测数据之差是否来自均值为 0 的总体（产生数据的总体是否具有相同的均值）。
具体步骤如下：
(1)对 i=1,...,n，计算 ∣Xi-M0∣，它们代表这些样本点到 M0 的距离。
(2)把上面的 n 个绝对值排序，并找出它们的 n 个秩，如果它们有相同的样本点，每个点取平均秩（如 1,4,4,5 的秩为 1,2.5,2.5,4）。
(3)令 W+等于 Xi-M0>0 的 ∣Xi-M0∣ 的秩的和，而 W-等于 Xi-M0<0 的 ∣Xi-M0∣ 的秩的和。
(4)对双边检验 H0：M=M0<=>H1：M≠M0，在零假设下，W+和 W-应差不多。因而，当其中之一很小时，应怀疑零假设。在此，取检验统计量 W=min(W+,W-)
(5)根据得到的 W 值，利用统计软件或查 Wilcoxon 符号秩检验的分布表以得到在零假设下的 p 值。如果 n 很大要用正态近似：得到一个与 W 有关的正态随机变量 Z 的值，再用软件或查正态分布表得到 p 值。
(6)如果 p 值较小（比如小于或等于给定的显著性水平，譬如 0.05）则可以拒绝零假设。如果 p 值较大则没有充分的证据来拒绝零假设，但不意味着接受零假设。
​

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]Fisher Box, Joan. Guinness, Gosset, Fisher, and Small Samples. Statistical Science. 1987, 2 (1): 45–52.
[3]王呼生，常沛．《新编医学计算机信息应用》．北京：中国铁道出版社，2016.07
[4]吴喜之 赵博娟．非参数统计：中国统计出版社，2011 年