独立样本MannWhitney检验

# 1、作用

MannWhitney 检验用于分析一个定类变量与一个或者多个定量变量之间有无明显差异，与独立样本 t 检验不同的是，MannWhitney 检验不需要数据呈现正态分布，需要特别注意的是，以上说到的定类变量为二分类变量（三分类及以上使用 Kruskal-Wallis 检验），各分类频数可以不相等。
​

# 2、输入输出描述

输入：一个定类变量 X（如学校字段，包括甲学校、乙学校）与定量字段 Y（如甲 40 名学生与乙学校 60 名学生的高考数学成绩）。
输出：模型检验的结果，如甲学校与乙学校的学生高考数学成绩存在/不存在显著性差异。
​

# 3、案例示例

示例：如研究不同学校的学生(各学校学生数不一定相等)成绩是否存在差异性。
​

# 4、案例数据

独立样本MannWhitney检验

# 5、案例操作

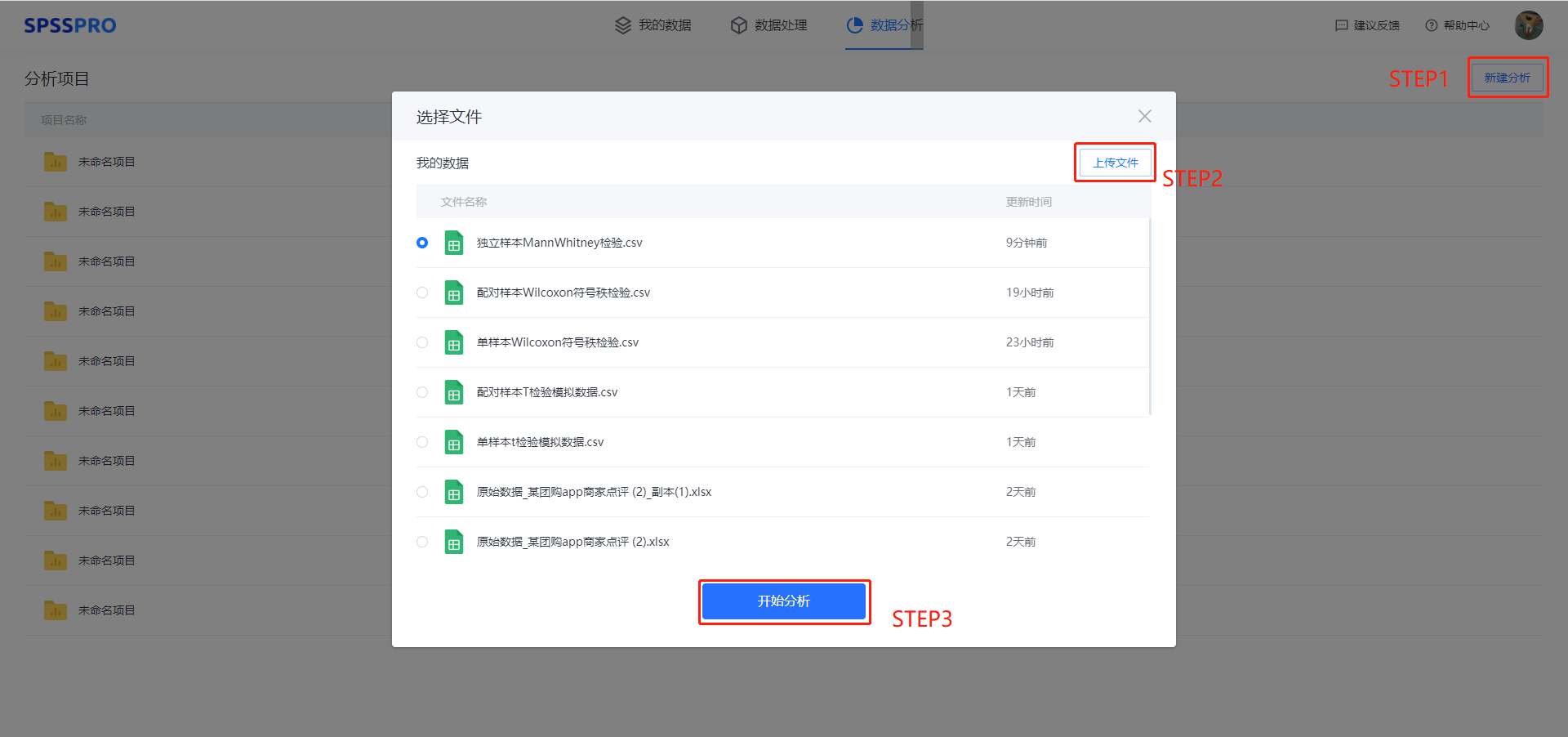
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【独立样本 MannWhitney 检验】；
step5：查看对应的数据数据格式，【独立样本 MannWhitney 检验】要求输入数据为定量变量，且至少有一项,另一个为定类变量，也是至少有一项；
step6：点击【开始分析】，完成全部操作；
​

# 6、输出结果分析

输出结果 1：正态性检验结果

​ 图表说明：因为成绩样本 N≥5000，故采用 K-S 检验，显著性 P 值为 0.000，水平上呈现显著性，拒绝原假设，因此数据不满足正态分布，可以进行独立样本 MannWhitney 检验，若数据满足正态分布则可以采用独立样本 T 检验。

输出结果 2：正态性检验直方图

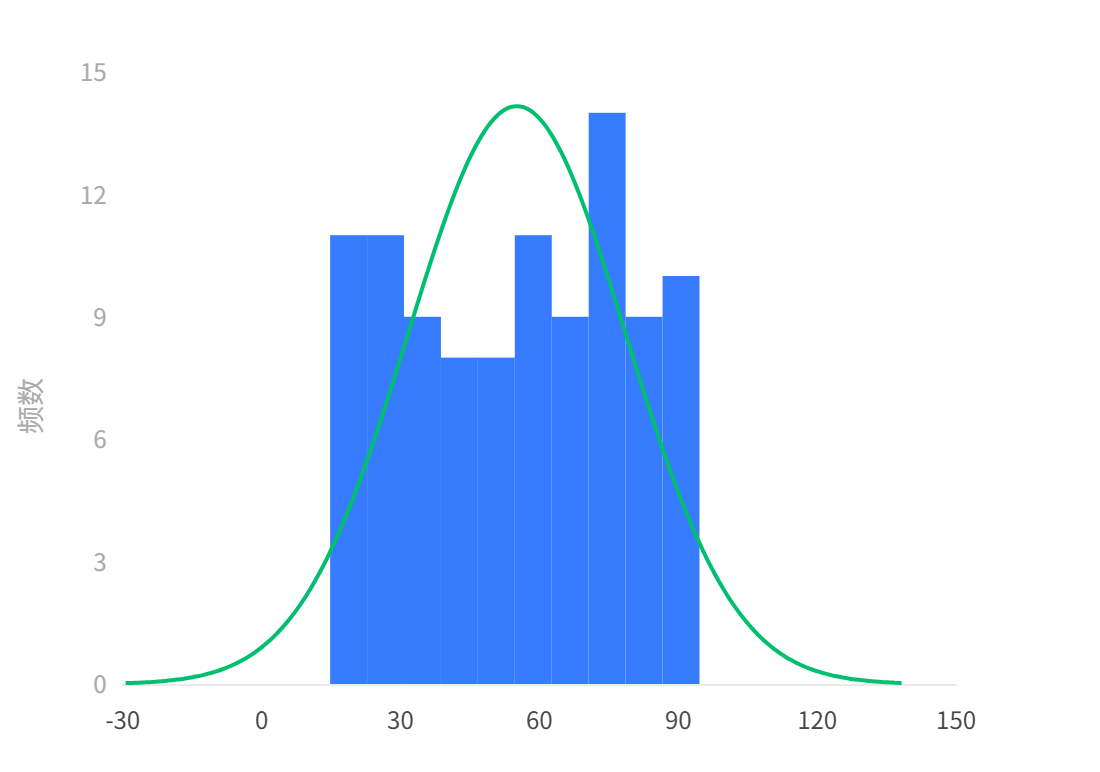
图表说明：上图展示了成绩数据的正态性检验直方图。从分布形态来看，数据未呈现正态分布的钟形特征，且在低分段0分出现明显峰值，30分后频数骤降，整体分布呈现左偏特征。结合直方图的非对称性和极端值，表明数据显著偏离正态性假设。因此，建议采用非参数检验方法Mann-Whitney U检验进行后续分析。
​

输出结果 3：MannWhitney U 检验分析结果表

图表说明：甲学校、乙学校在成绩上的中位数分别为：55.919/57.182，差异极小（差值1.263）。两校标准差接近（甲校23.434，乙校23.824），表明数据分布相似。Mann-Whitney U检验统计量为1185，对应 $p=0.916$，远高于显著性阈值（$\alpha =0.05$），统计结果不显著，说明两校成绩无统计学差异。其差异幅度 Cohen's d 值为0.032，远小于0.2的阈值，表明实际差异幅度可忽略不计。
​

输出结果 4：MannWhitney U 检验频率直方图

图表说明：由上图可以直观发现，甲学校成绩在较高分段的频数显著集中，整体分布呈现右偏特征；乙学校成绩主要分布在低分段，但中间分段存在少量分散分布。两校成绩分布形态差异明显，甲学校整体成绩偏高且集中，乙学校成绩分布范围更广且偏低，表明两校成绩存在显著分层现象。
​

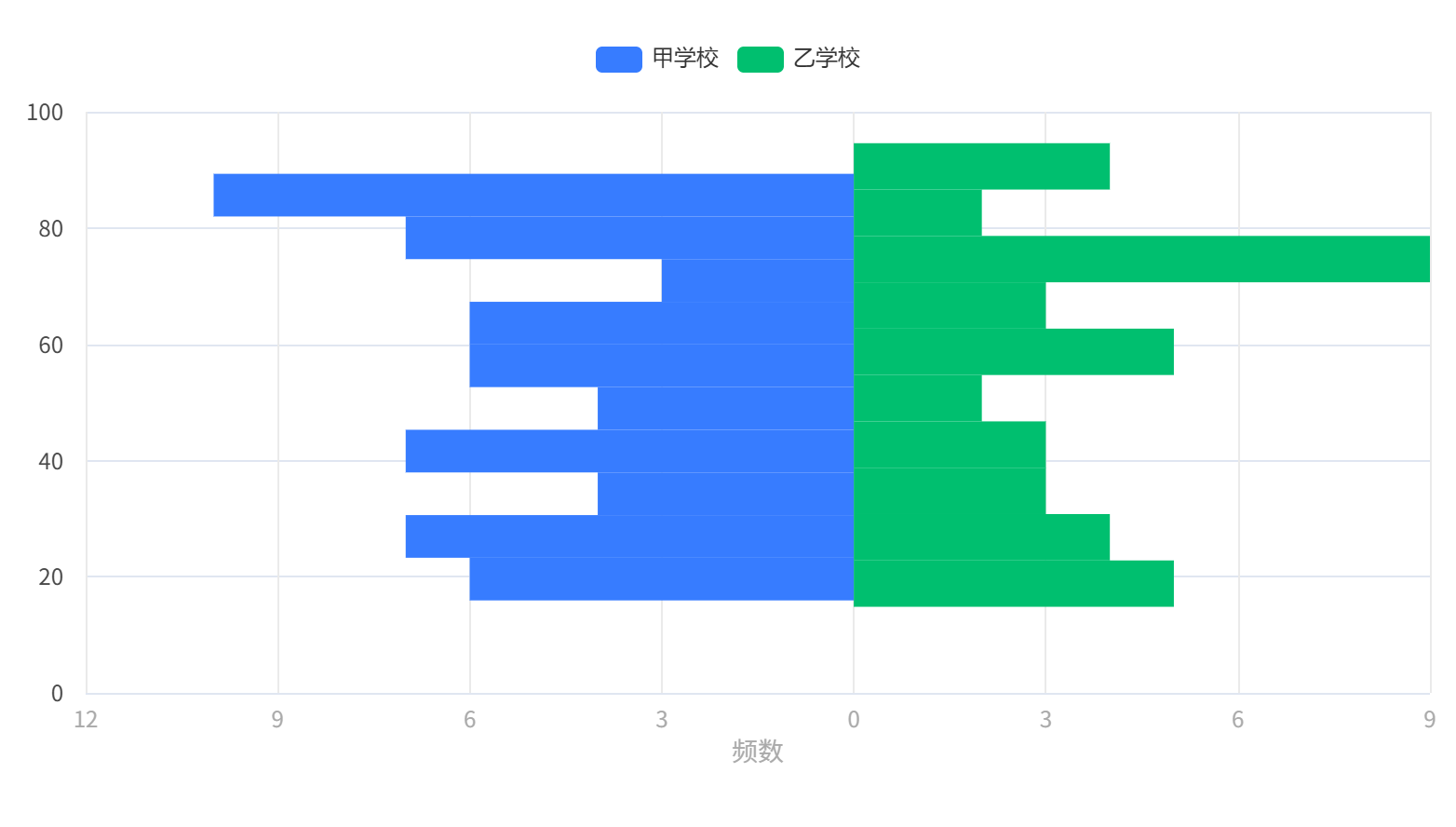
# 7、注意事项

• 独立样本 MannWhitney 检验中的两分类样本数量可以不一样，如果超过三个分类，则采用使用 Kruskal-Wallis 检验。
• 各差异性分析模型的使用场景如下总结：

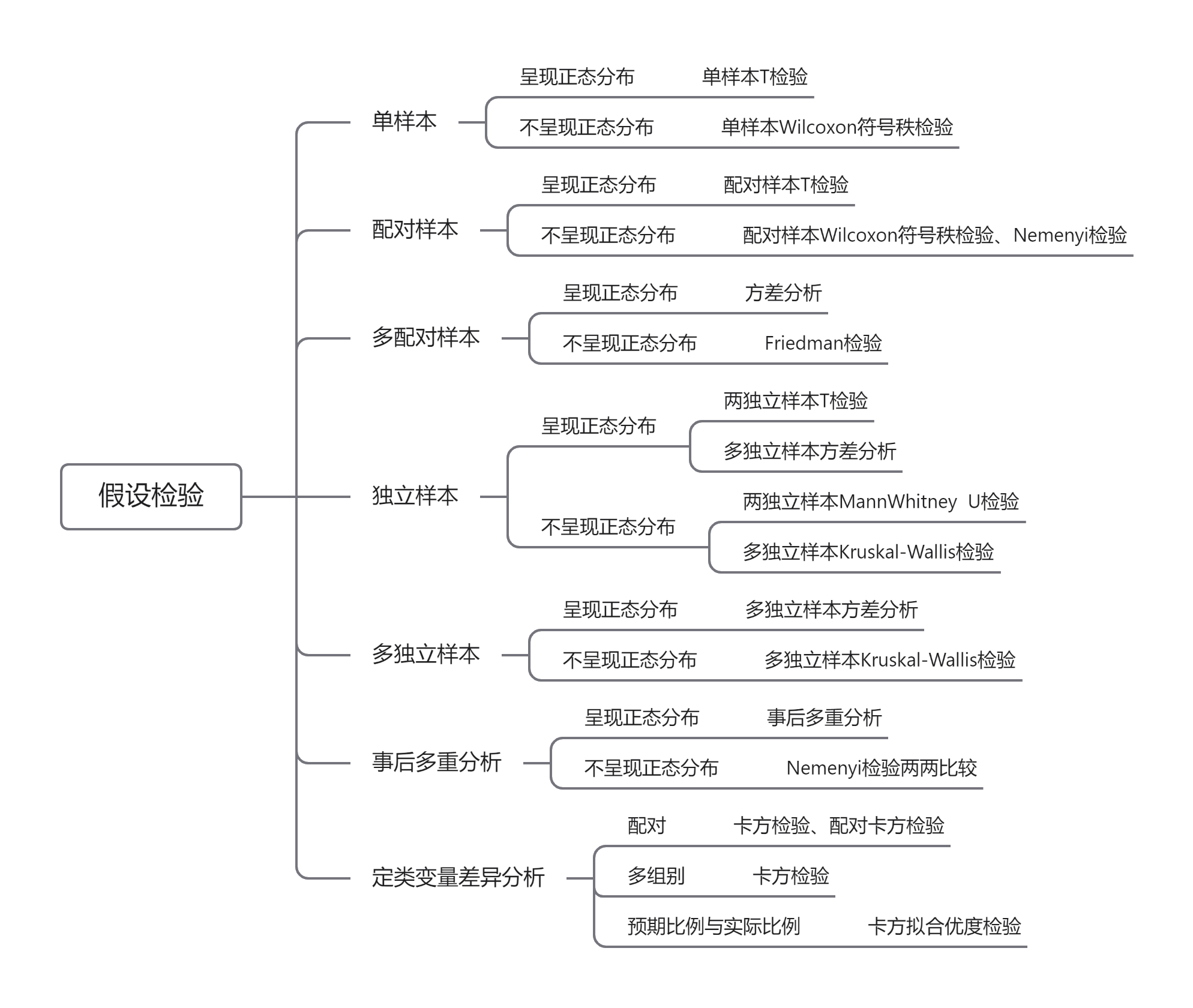
# 8、模型理论

Mann-Whitney 检验，又称符号等级检验，是一种非参数检验。
其计算方式如下：
设两个样本的数据量分布为 n1 和 n2，再令 R1 代表样本 1 的秩和，R2 代表样本 2 的秩和：

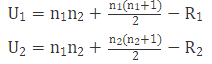
在检验时令：U=MIN(U1,U2),则当样本较大时

U的抽样分布迅速接近正态分布

或者使用等价公式不使用绝对值符号：

求出Z值后，查表即可判断两个样本的均值差异显著性。

# 9、手推步骤

# Step 1：数据合并并计算秩和

原始数据：

• 甲学校样本量 $n_1=60$
• 乙学校样本量 $n_2=40$

甲学校秩和 $R_1$：$R_1=2+3+5+\cdots +98+100=3045$
乙学校秩和 $R_2$：$R_2=\frac{(n_1+n_2)(n_1+n_2+1)}{2}-R_1=\frac{100\times 101}{2}-3045=5050-3045=2005$

# Step 2：计算 $U$ 值

公式：

$U_1=n_1{n}_2+\frac{n_1(n_1+1)}{2}-R_1=60\times 40+\frac{60\times 61}{2}-3045=2400+1830-3045=1185$

$U_2=n_1{n}_2+\frac{n_2(n_2+1)}{2}-R_2=60\times 40+\frac{40\times 41}{2}-2005=2400+820-2005=1215$

最终 $U$ 值：$U=min(U_1,U_2)=1185$

# Step 3：计算 $Z$ 值与 $P$ 值

$Z$ 值公式:

$Z=\frac{|U-\frac{n_1{n}_2}{2}|}{\sqrt{\frac{n_1{n}_2(n_1+n_2+1)}{12}}}=\frac{|1185-1200|}{\sqrt{\frac{60\times 40\times 101}{12}}}=\frac{15}{\sqrt{20200}}\approx 0.105$

查标准正态分布表：

• 单尾P值 $P(Z>0.105)\approx 0.458$
• 双尾P值 $2\times 0.458=0.916$

# Step 4：效应量（$Cohe{n}^{\prime }sd$）

计算过程：

$\text{Cohen’s }d=\frac{\text{中位数差值}}{\text{合并标准差}}=\frac{57.182-55.919}{23.473}\approx 0.032$

结论：甲学校与乙学校的成绩中位数无显著差异（$P=0.916$），差异幅度极小（$d=0.032$）。

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]杨维康,乔建芳,高行宜,钟文勤.秩和检验在鸟类栖息地选择分析中的运用[J].干旱区研究,2001(03):42-44.