多独立样本Kruskal-Wallis检验

操作视频

# 1、作用

多独立样本 Kruskal-Wallis 检验用于定类字段（X）与 1 个或 1 个以上的定量字段（Y，不需要正态分布）之间的差异性研究。需要注意的是，Kruskal-Wallis 检验可用于多分类定类字段数据的差异性分析，MannWhitney U 检验只能作用于二分类定类变量。

# 2、输入输出描述

输入：一个定类字段（如受教育程度）、一个或多个定量字段（如工资、家庭年收入）。
输出：模型检验的结果：同一因素不同分组（如：不同的受教育程度 X）对定量变量（如：工资 Y）产生/不产生显著性影响。

# 3、案例示例

示例：分析个人受教育程度（定类变量）是否给个人的经济收入（定量变量）带来显著性影响。

# 4、案例数据

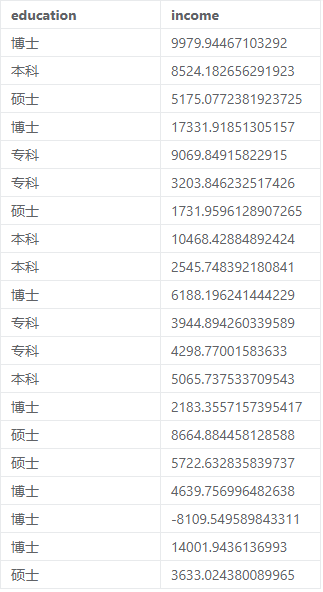
多独立样本Kruskal-Wallis检验案例数据

# 5、案例操作

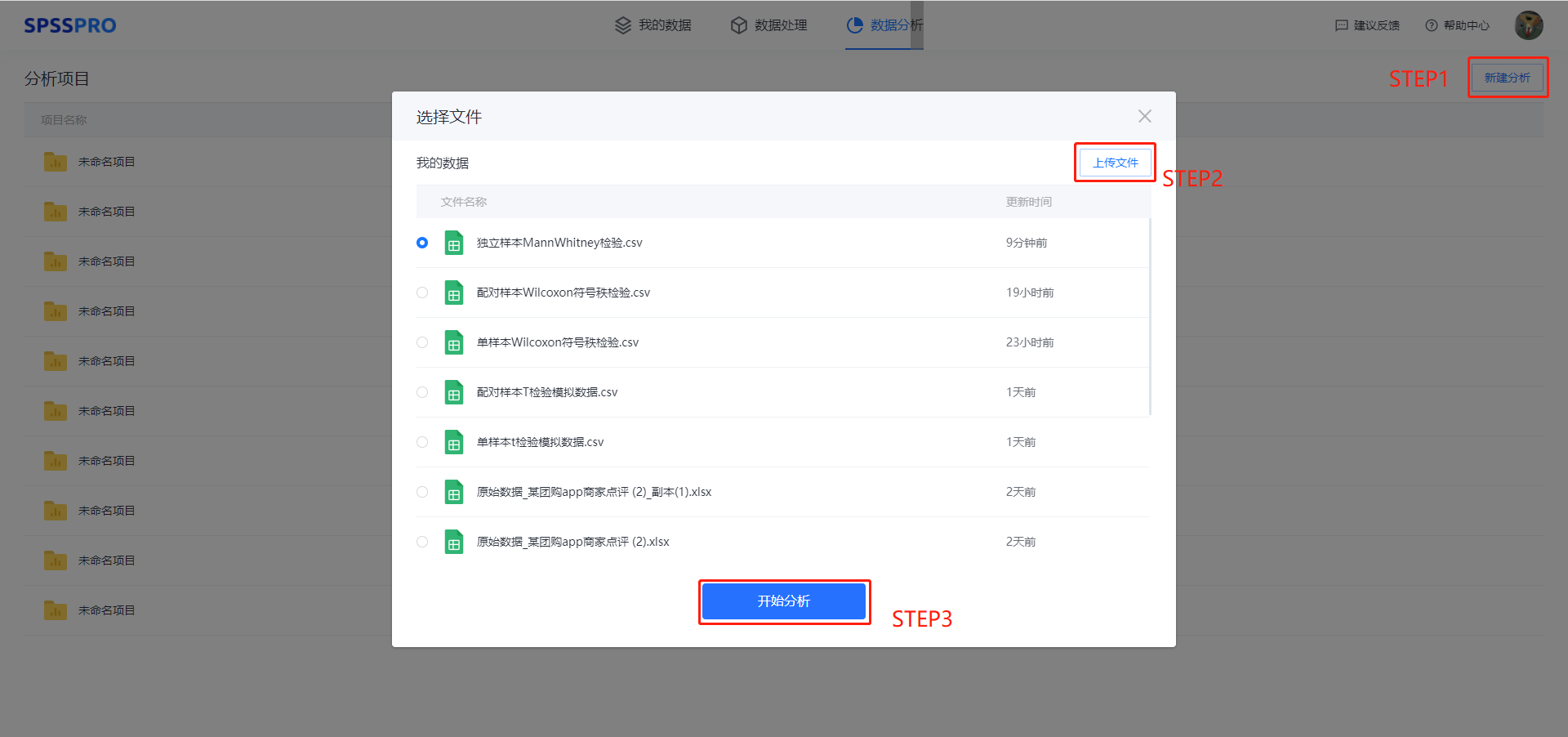
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；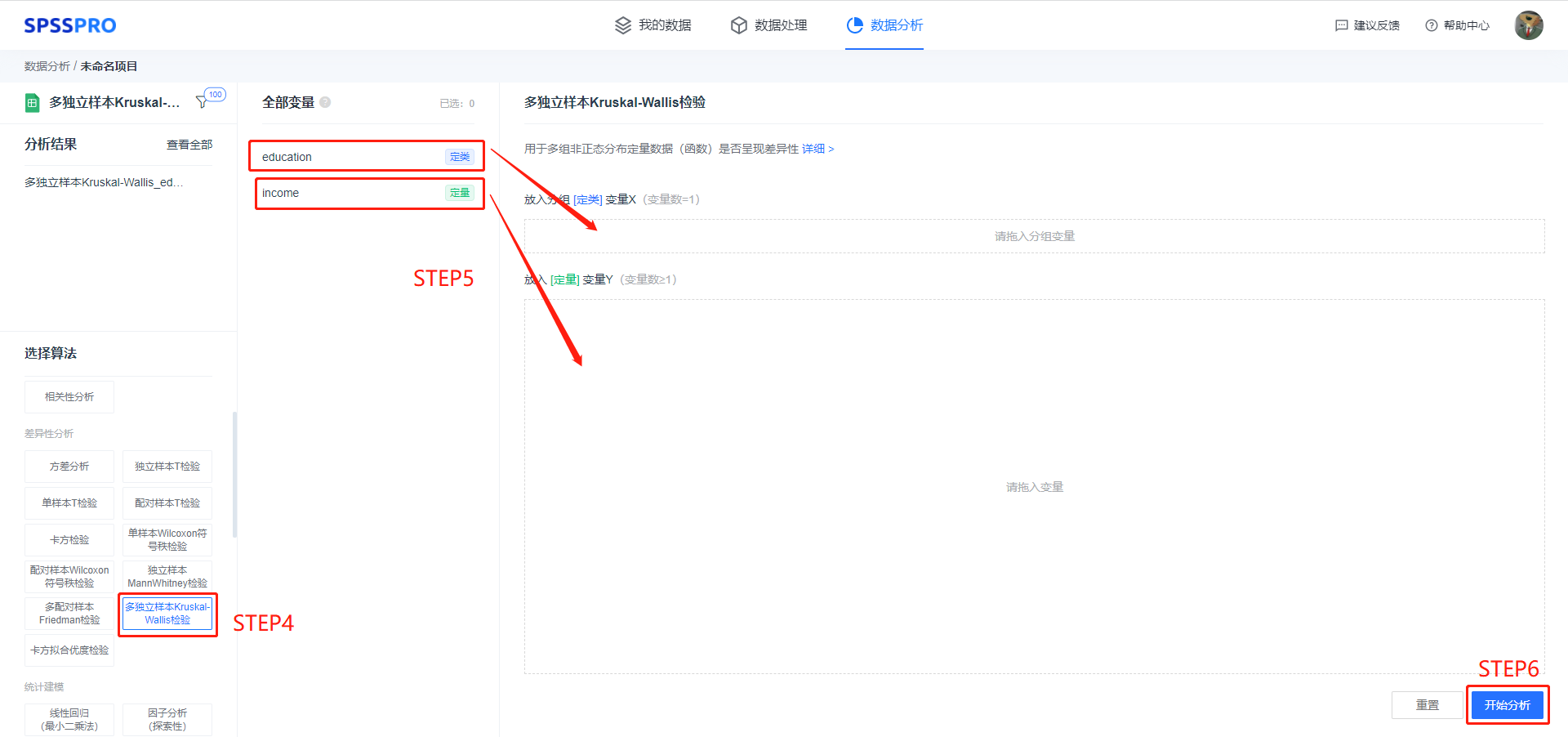

step4：选择【多独立样本 Kruskal-Wallis 检验】；
step5：查看对应的数据数据格式，【多独立样本 Kruskal-Wallis 检验】要求输入数据为定量变量，且至少有一项,另一个为定类变量，也是至少有一项；
step6：点击【开始分析】，完成全部操作；

# 6、输出结果分析

输出结果 1： 正态性检验结果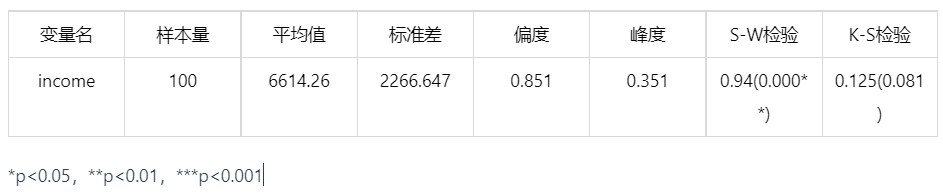

图表说明：
收入样本数量 N≥5000，故采用 K-S 检验，显著性 P 值为 0.081，水平上不呈现显著性，不能拒绝原假设，因此数据不满足正态分布。故进行多独立样本 Kruskal-Wallis 检验，满足正态分时，则使用多独立样本方差分析。

输出结果 2： 正态性检验直方图

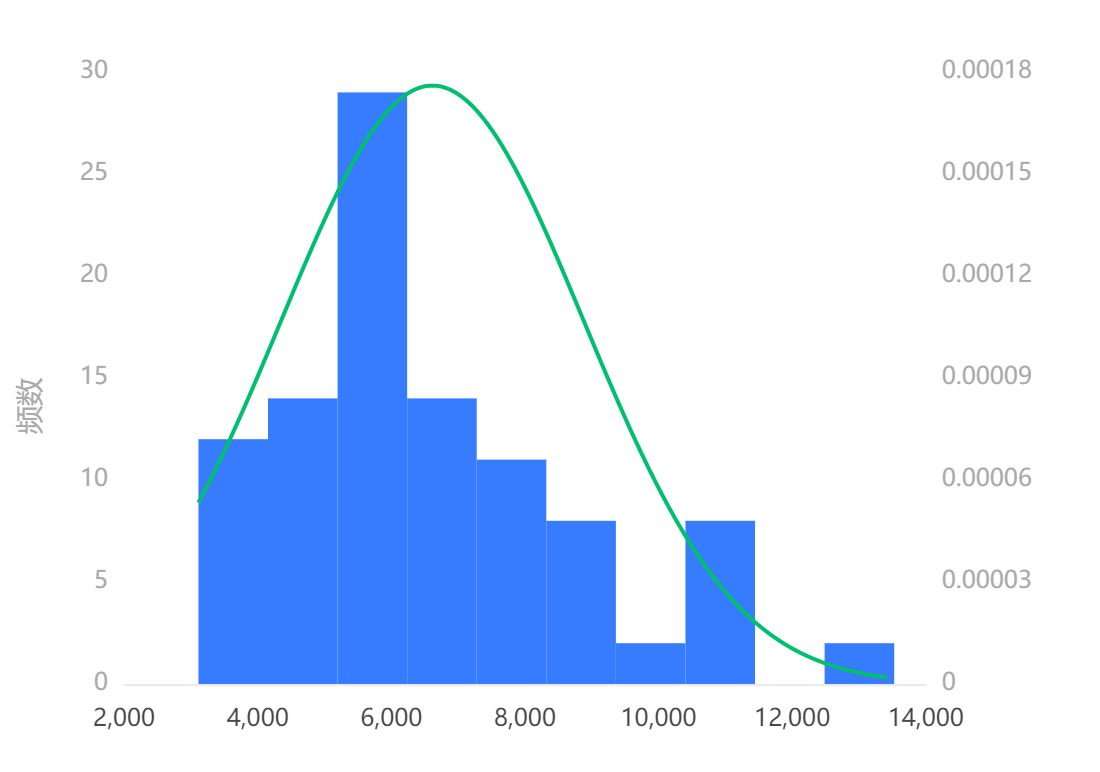
图表说明：上图展示了数据正态性检验的结果，正态图 10000 以下占比多，不呈现正态分布的钟形曲线，故可认为收入不是一个正态分布，可继续进行多独立样本 Kruskal-Wallis 检验。

**输出结果 3：**Kruskal-Wallis 检验分析结果表

图表说明：Kruskal-Wallis 检验结果显示，基于收入，检验结果 p 值为 0(<0.05)，因此统计结果显著，说明不同受教育程度在收入上存在显著差异。
其差异幅度 Cohen's f 值为：0.113，差异幅度非常小。

输出结果 4：事后多重分析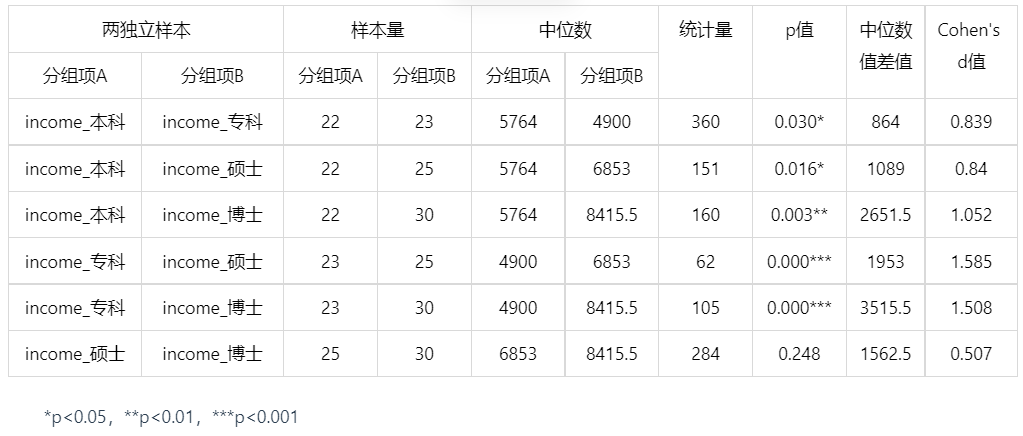

图表说明：
多独立样本 Kruskal-Wallis 检验只能检验是否具有差异性，接下来进行事后多重分析以判断是哪两组变量产生了差异。
本科、专科在 income 上的中位数分别为：5764.0/4900.0；检验结果 p 值为 0.030<0.05，因此统计结果显著，说明本科、专科在 income 上存在显著差异；其差异幅度 Cohen's f 值为：0.839，差异幅度非常大。
本科、硕士在 income 上的中位数分别为：5764.0/6853.0；检验结果 p 值为 0.016<0.05，因此统计结果显著，说明本科、硕士在 income 上存在显著差异；其差异幅度 Cohen's f 值为：0.84，差异幅度非常大。
本科、博士在 income 上的中位数分别为：5764.0/8415.5；检验结果 p 值为 0.003<0.05，因此统计结果显著，说明本科、博士在 income 上存在显著差异；其差异幅度 Cohen's f 值为：1.052，差异幅度非常大。
专科、硕士在 income 上的中位数分别为：4900.0/6853.0；检验结果 p 值为 0<0.05，因此统计结果显著，说明专科、硕士在 income 上存在显著差异；其差异幅度 Cohen's f 值为：1.585，差异幅度非常大。
专科、博士在 income 上的中位数分别为：4900.0/8415.5；检验结果 p 值为 0<0.05，因此统计结果显著，说明专科、博士在 income 上存在显著差异；其差异幅度 Cohen's f 值为：1.508，差异幅度非常大。
硕士、博士在 income 上的中位数分别为：6853.0/8415.5；检验结果 p 值为 0.25>0.05，因此统计结果不显著，说明硕士、博士在 income 上不存在显著差异；其差异幅度 Cohen's f 值为：0.507，差异幅度中等。
根据以上结果，可知，除去硕博的差异幅度是中等以外，其他的差异幅度都相当的大，可见学历的重要性。

# 7、注意事项

当定量变量非正态且定类变量超过二分类采用 Kruskal-Wallis 检验，二分类则采用 MannWhitney U 检验。
当定量变量为正态可采用多独立样本方差分析。
各差异性分析模型的使用场景如下总结：

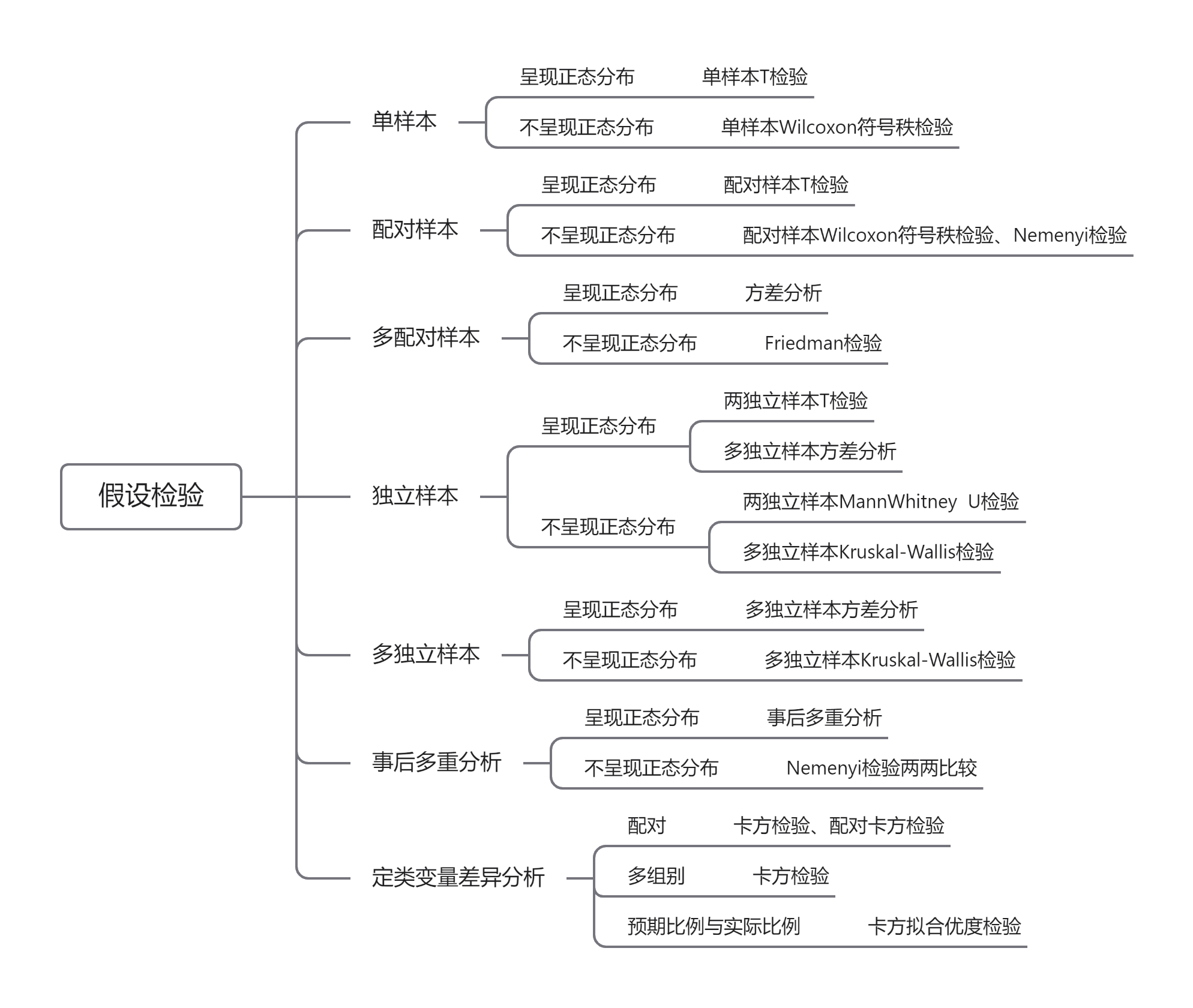
# 8、模型理论

多独立样本 Kruskal-Wallis 检验（又称 H 检验）的实质上是两独立样本时的 Mann-Whitney U 检验在多个独立样本下的推广，用于检验多个总体的分布是否存在显著差异。其原假设是：多个独立样本来自的多个总体的分布无显著差异。多独立样本 Kruskal-Wallis 检验的基本思想是：
首先，将多组样本数混合并按升序排序，求出各变量值的秩；然后，考察各组秩的均值是否存在显著差异。如果各组秩的均值不存在显著差异，则认为多组数据充分混合，数值相差不大，可以认为多个总体的分布无显著差异；反之，如果各组秩的均值存在显著差异，则是多组数据无法混合，有些组的数值普遍偏大，有些组的数值普遍偏小，可认为多个总体的分布存在显著差异，至少有一个样本不同于其他样本。为研究各组的秩差异，可借鉴方差分析的方法。
方差分析认为，各样本组秩的总变差一方面源于各样本组之间的差异（组间差），另一方面源于各样本组内的抽样误差（组内差）。如果各样本组秩的总变差的大部分可由组间差解释，则表明各样本组的总体分布存在显著差异；反之，如果各样本组秩的总变差的大部分不能由组间差解释，则表明各样本组的总体分布没有显著差异。
由上可以得出多独立样本非参数检验的目的（由独立样本数据推断多个总体的分布是否存在显著差异），基本假设（H0：多个总体分布无显著差异），数据要求（样本数据和分组标志）。
基于以上思路可以构造 K-W 统计量，即

需要检验的原假设为各组之间不存在差异，或者说各组的样本来自的总体具有相同的中心或均值或中位数。在原假设为真时，各组样本的秩平均应该与全体样本的秩平均

比较接近。
所以组间平方和为:

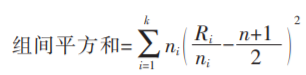
恰好是刻画这种接近程度的一个统计量，除以全体样本秩方差的平均，可以消除量纲的影响。样本方差的自由度为 n-1。所以

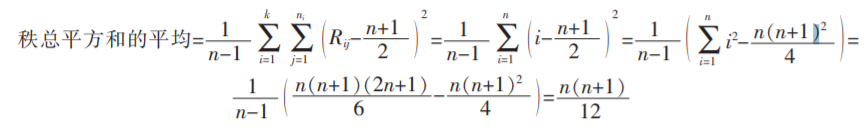
因此，Kruskal-Wallis 秩和统计量 K-W 为

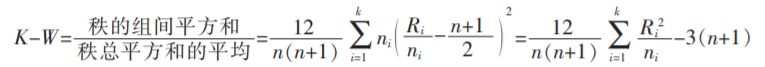
其中 k 为样本组数，n 是总样本量，ni 是第 i 组的样本量；Ri 是第 i 组样本中的秩总和，Rij 是第 i 组样本中的
第 j 个观察值的秩值。
如果样本中存在结值，需要调整公式中的 K-W 统计量，校正系数 C 为:

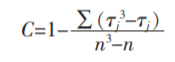
其中 τj 是第 j 个结值的个数。调整后的 KWc 统计量为

如果每组样本中的观察数目至少有 5 个，那么样本统计量 KWc 非常接近自由度为 k-1 的卡方分布。因此，用卡方分布来决定 KWc 统计量的检验。

# 9、手推步骤

# Step 1：数据整理和计算各组秩和（ $R_{i}$ ）

将收入数据，按升序排列，处理重复值后分配平均秩。
整理完整计算后各组秩和为：

本科组： $R_{1} = 1200$
专科组： $R_{2} = 800$
硕士组： $R_{3} = 1500$
博士组： $R_{4} = 2500$

# Step 2：计算 $K - W$ 统计量

公式：

$K - W = \frac{12}{N (N + 1)} \sum_{i = 1}^{k} \frac{R_{i}^{2}}{n_{i}} - 3 (N + 1)$

代入数据：

N = 100

，

k = 4

$\sum \frac{R_{i}^{2}}{n_{i}} = \frac{1200^{2}}{22} + \frac{800^{2}}{23} + \frac{1500^{2}}{25} + \frac{2500^{2}}{30} \approx 391, 613.97$

计算：

$K - W = \frac{12}{100 \times 101} \times 391, 613.97 - 3 \times 101 \approx 31.93$

# Step 3：校正结的影响

存在5个重复值（每个重复2次）：

$C = 1 - \frac{5 \times (2^{3} - 2)}{100^{3} - 100} \approx 0.999$

校正后统计量：

$K W_{c} = \frac{31.93}{0.999} \approx 31.97$

# Step 4：假设检验

自由度： $d f = 4 - 1 = 3$
卡方临界值（ $α = 0.05$ ）：7.815
结论： $K W_{c} = 31.97 > 7.815$ ，拒绝原假设，不同教育程度在收入上存在显著差异。

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]Conover W J. Practical Nonparametric Statistics[M]. 2th ed. New York：John Wiley &Sons，Inc，1980.
[3]张林泉.多独立样本 Kruskal-Wallis 检验的原理及其实证分析[J].苏州科技学院学报(自然科学版),2014,31(01):14-16+38.

建议反馈