卡方检验

操作视频

# 卡方检验

# 1、作用

在卡方检验中，最常用的就是Pearson卡方检验（Pearson's chi-squared test），它是一种非参数检验，适用于定类变量之间的关联性分析，可以用于衡量观察值与期望值之间偏离程度的统计检验方法。通过统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为 0，表明理论值完全符合。

Pearson卡方检验有两种类型：适配度检验和独立性检验。

适配度检验（chi-square goodness of fit best），即卡方拟合优度检验，常用于只有一个分类变量时，用于验证一组定类数据观察值的频数分配是否异于理论上的分布。在通常情况下，我们常期望各类型具有相同的比例。

独立性检验(chi-square test of independence) 是用于验证两个分类变量是否互相独立。

# 2、输入输出描述

输入：一个定类变量 X（如学校字段，包括甲学校、乙学校）与定类字段 Y（如甲学校 40 名学生与乙学校 60 名学生的体育成绩等级）

输出：模型检验的结果，如甲学校与乙学校的学生体育成绩等级存在/不存在显著性差异

# 3、案例示例

从某高中学随机抽取两个以上的班级，调查他们对待文理分科的态度是否有显著差异。

# 4、案例数据

卡方检验案例数据

# 5、案例操作

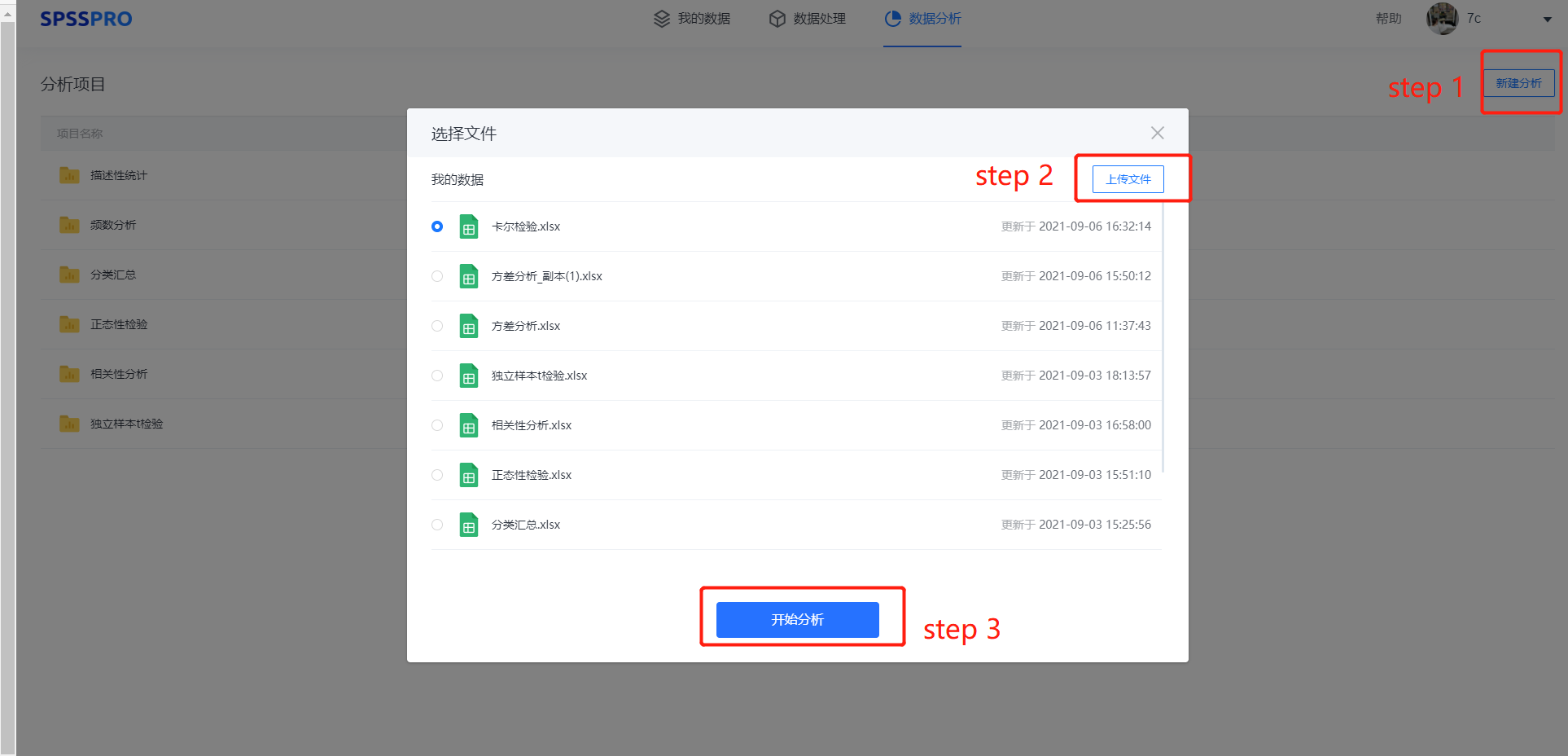
卡方检验上传数据

Step1：新建分析；

Step2：上传数据；

Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

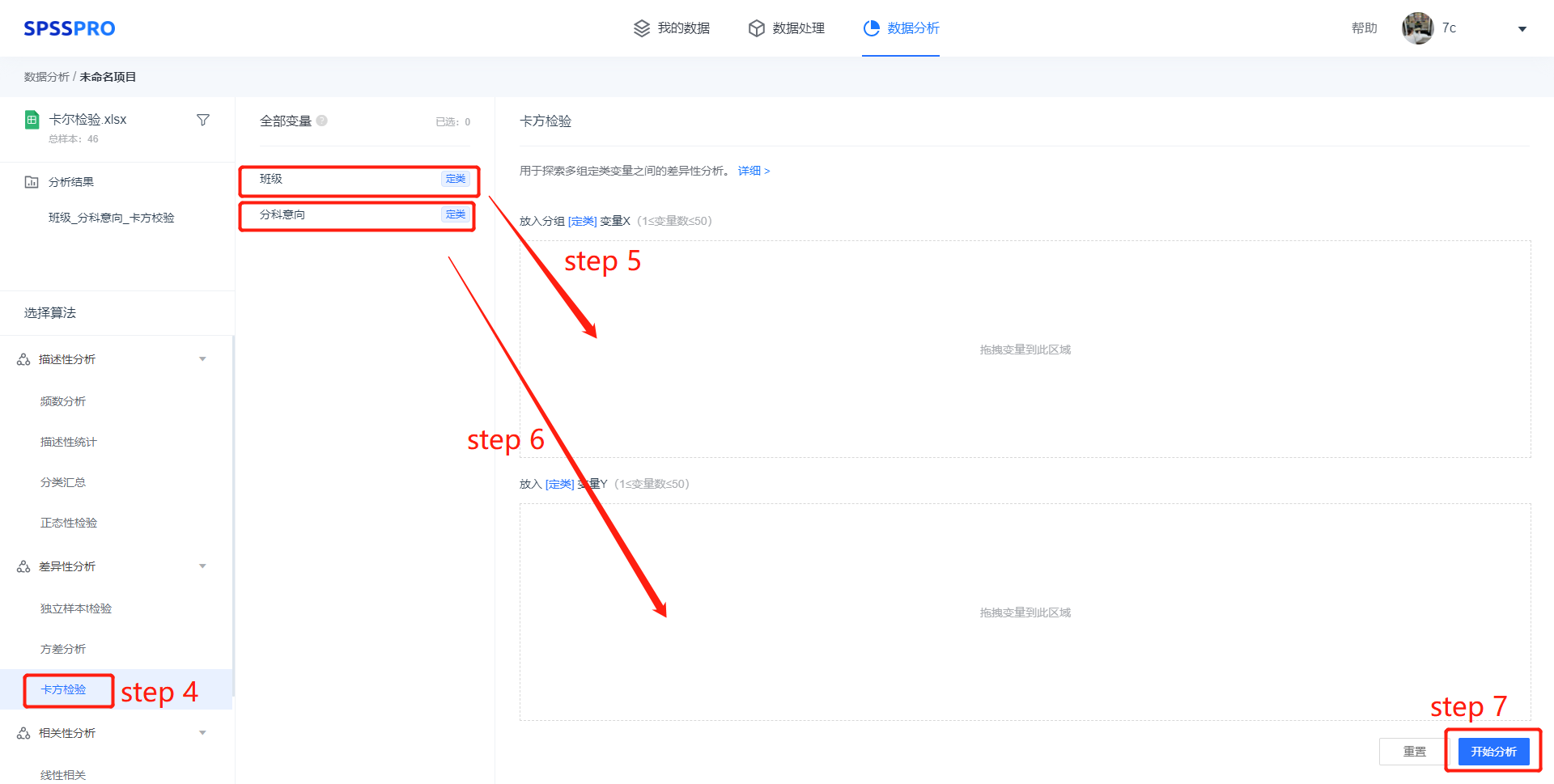
卡方检验操作

step4：选择【卡方检验】；

step5-6：查看对应的数据数据格式，【卡方检验】要求输入数据为分组定类变量 X，（1≤ 变量数 ≤50）；放入定量变量量 Y（1≤ 变量数 ≤50）；

step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：卡方检验分析结果

题目	名称	班级		总计	X²	校正 X²	P
		1.0	2.0
分科意向	1.0	8	16	24	3.069	2.119	0.080
	2.0	13	9	22

图表说明：上表展示了模型检验的结果，包括数据的频数、频数百分比、卡方值、显著性 P 值。P 值小于 0.01。卡方检验分析的结果显示，对于班级，显著性 P 值为 0.080，水平上不呈现显著性，接受原假设，因此对于班级和分科意向数据不存在显著性差异。

输出结果 2：卡方交叉热力图

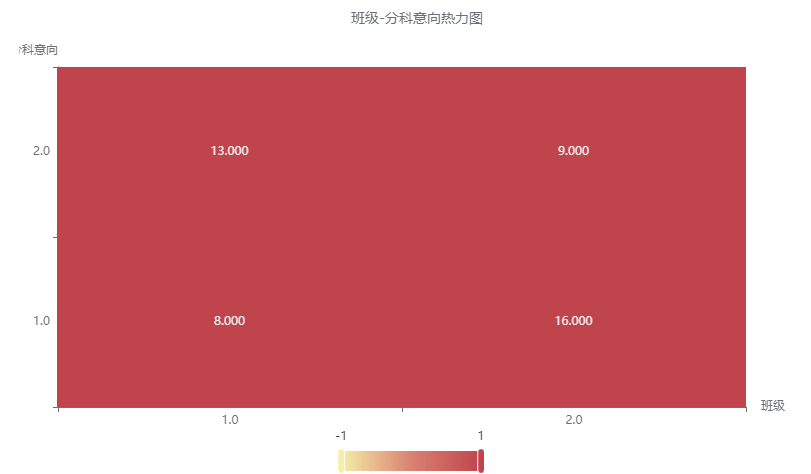
卡方交叉热力图

图表说明：上图展示了热力图的形式展示了交叉列联表的值，主要通过颜色深浅去表示值的大小。

输出结果 3：效应量化分析

字段名/分析项	Phi	Crammer's V	列联系数	lambda
分科意向	0.258	0.258	0.250	0.227

图表说明：上表展示了效应量化分析的结果，包括 phi、Crammer's V、列联系数、lambda ，用于分析样本的相关程度。效应量化分析的结果显示，分析项：分科意向 Cramer’s V 值为 0.2583106399751794，因此分科意向和班级的差异程度为中等程度差异。

# 7、注意事项

科学文献中，当提及卡方检验而没有特别指明类型时，通常即指皮尔森卡方检验，SPSSPRO 的卡方检验默认为皮尔逊卡方检验；

# 8、模型理论

当满足以下要求时，可以使用Pearson卡方检验：

（1）变量为定类变量

（2）样本是从总体中随机抽取的

（3）每个组中都至少有5个观测值

Pearson卡方检验通用的分析步骤如下：

（1）制作列联表，统计观察频数

（2）提出假设，设置显著性水平

（3）计算统计量，包括理论频数、 $x^{2}$ 统计值和自由度

x^{2} = \sum \frac{(O - E)^{2}}{E}

其中，O为实际的观测频数，E为理论频数

（3）查表得p值，与 $x^{2}$ 值进行比较，得出结论

若p<a，则拒绝原假设，接受备择假设；若p>a,则不拒绝原假设。

适配度检验分析步骤如下：

（1）提出原假设，设置显著性水平

H0：各个类别具有相同的比例

H1：各个类别的比例不全相同

a 通常可以用0.01,0.05,或0.1

（2）计算统计量。

理论频数：

E_{i} = \frac{N}{m}

其中，m为m个类别，N为总观察值；

$x^{2}$ 统计值：

x^{2} = \sum \frac{(O - E)^{2}}{E}

自由度：

d f = m - 1

(3) 查表得p值，与 $x^{2}$ 值进行比较，得出结论

若p<a，则拒绝原假设，接受备择假设,认为各类别不具有相同的比例；若p>a,则不拒绝原假设，暂时没有证据认为各类别具有不同的比例。

独立性检验分析步骤如下：

（1）提出假设，设置显著性水平

H0：变量A与变量B之间相互独立

H1：变量A与变量B不独立

a 通常可以用0.01,0.05,或0.1

（2）计算统计值

期望次数：

E_{i, j} = \frac{\sum_{n_{c} = 1}^{c} O_{i, n_{c}} * \sum_{n_{r} = 1}^{r} O_{n_{r}, j}}{N}

其中，r和c表示该列联表中共有r行c列； $O$ 为原始数据；N为总样本数。

$x^{2}$ 统计值为：

x^{2} = \sum_{i = 1}^{r} \sum_{j = 1}^{c} \frac{(O_{i, j} - E_{i, j})^{2}}{E_{i, j}}

自由度为：

d f = \frac{r - 1}{c - 1}

(3) 查表得p值，与 $x^{2}$ 值进行比较，得出结论

若p<a，则拒绝原假设，接受备择假设,认为两变量之间相互独立；若p>a,则不拒绝原假设，暂时没有证据认为变量之间具有相关性。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]茆诗松, 王静龙, 濮晓龙, 等. 高等数理统计 (第二版)[M]. 北京: 高等教育出版社, 2006.
[3]陆运清. 用 Pearson's 卡方统计量进行统计检验时应注意的问题[J]. 统计与决策, 2009 (15): 32-33.

建议反馈