多配对样本Friedman检验

操作视频

SPSSPRO教程-多配对样本Friedman检验

# 1、作用

Friedman 检验用于分析多组样本数一致的定量变量之间有无明显差异，需要特别注意的是，这些定量变量适用于非正态分布，如果变量数据呈现正态分布，建议选择方差分析。

# 2、输入输出描述

输入：样本数相同，且差值不呈现正态分布的两个定量变量。
输出：这两个定量变量是否存在差异性。

# 3、案例示例

示例：检验某医院 50 个病人注射某药剂第一、二、三、四周的血压是否一致。

# 4、案例数据

多配对样本 Friedman 检验案例数据

# 5、案例操作

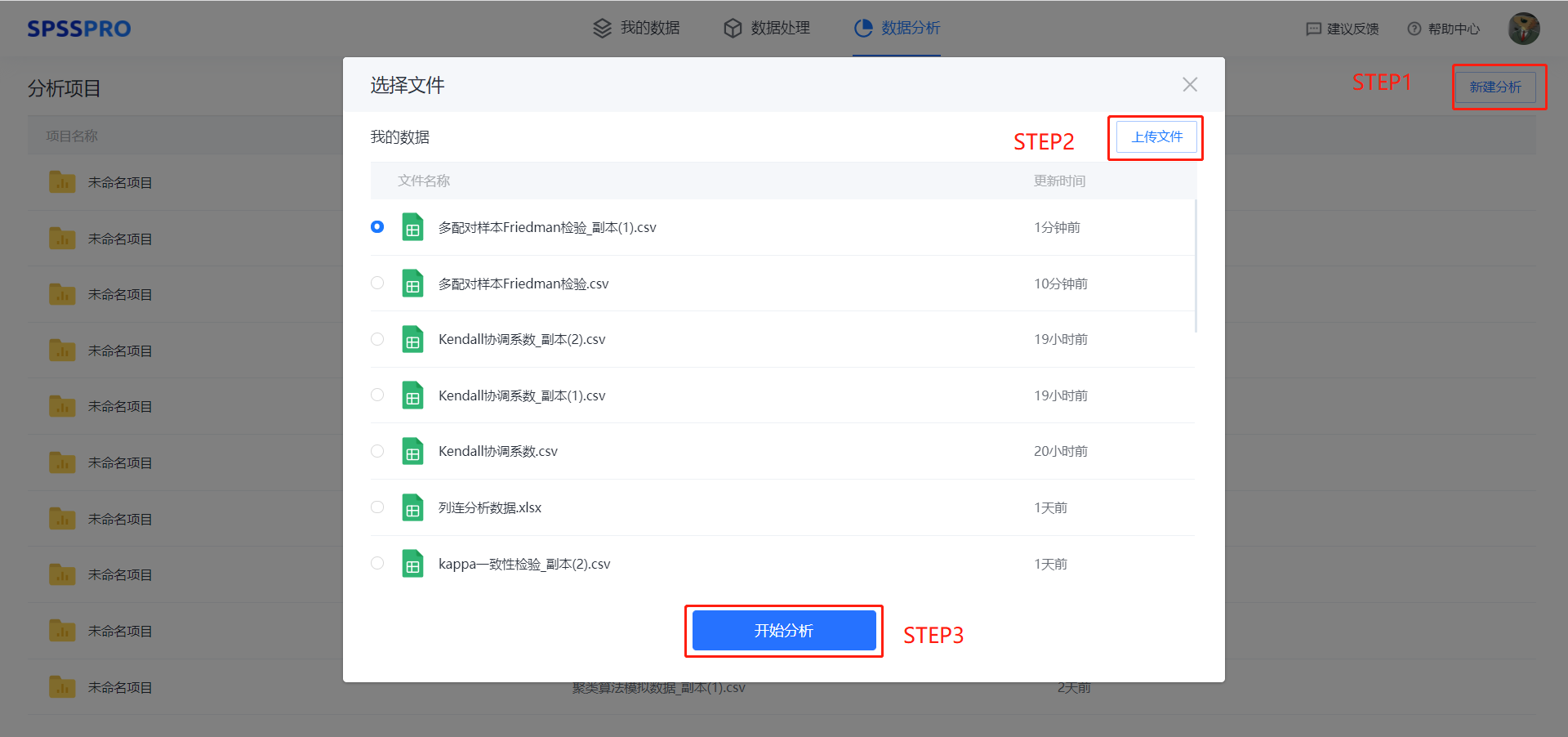
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；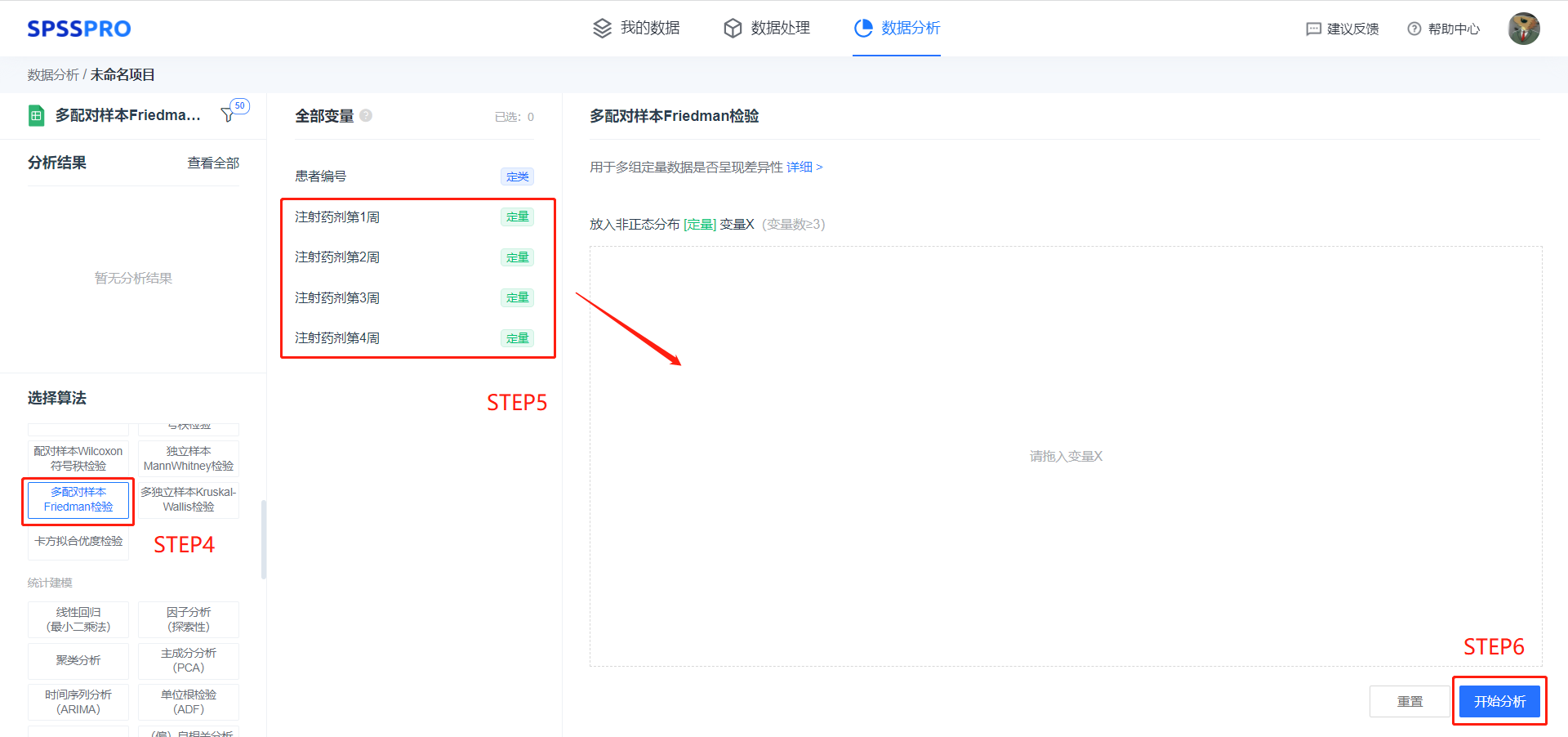

step4：选择【多配对样本 Friedman 检验】；
step5：查看对应的数据数据格式，【多配对样本 Friedman 检验】要求输入数据为定量变量，且至少有三项；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：正态性检验结果

图表说明：
一般进行正态性检验时有两种方法：Shapiro-Wilk 检验，适用于小样本资料（样本量 ≤5000）；另一种是 Kolmogorov–Smirnov 检验，适用于大样本资料（样本量>5000）; 若呈现显著性（p<0.05 或 0.01），则说明拒绝原假设（数据符合正态分布），该数据不满足正态分布，反之则说明该数据满足正态分布。
注射药剂第各周样本量为 100，小于 5000，故采用 S-W 检验，显著性 P 值为 0.008**，水平上不呈现显著性，不能拒绝原假设，因此数据不满足正态分布，可以进行 Friedman 检验。

输出结果 2：正态性检验直方图

图表说明：上图展示了定量变量服药前血压、服药后血压的差值数据正态性检验的结果：
以第一周为例，由图可得，数据不满足正态分布，可以进行 Friedman 检验。

输出结果 3：Friedman 检验分析结果表

图表说明：通过 Friedman 检验分析结果表可知，显著性 p 值为 0.000<0.05,因此统计结果显著，说明注射药剂第 1 周、注射药剂第 2 周、注射药剂第 3 周、注射药剂第 4 周之间存在显著差异；
其差异幅度 Cohen's f 值为：0.229，差异幅度较小。

输出结果 4：箱线图对比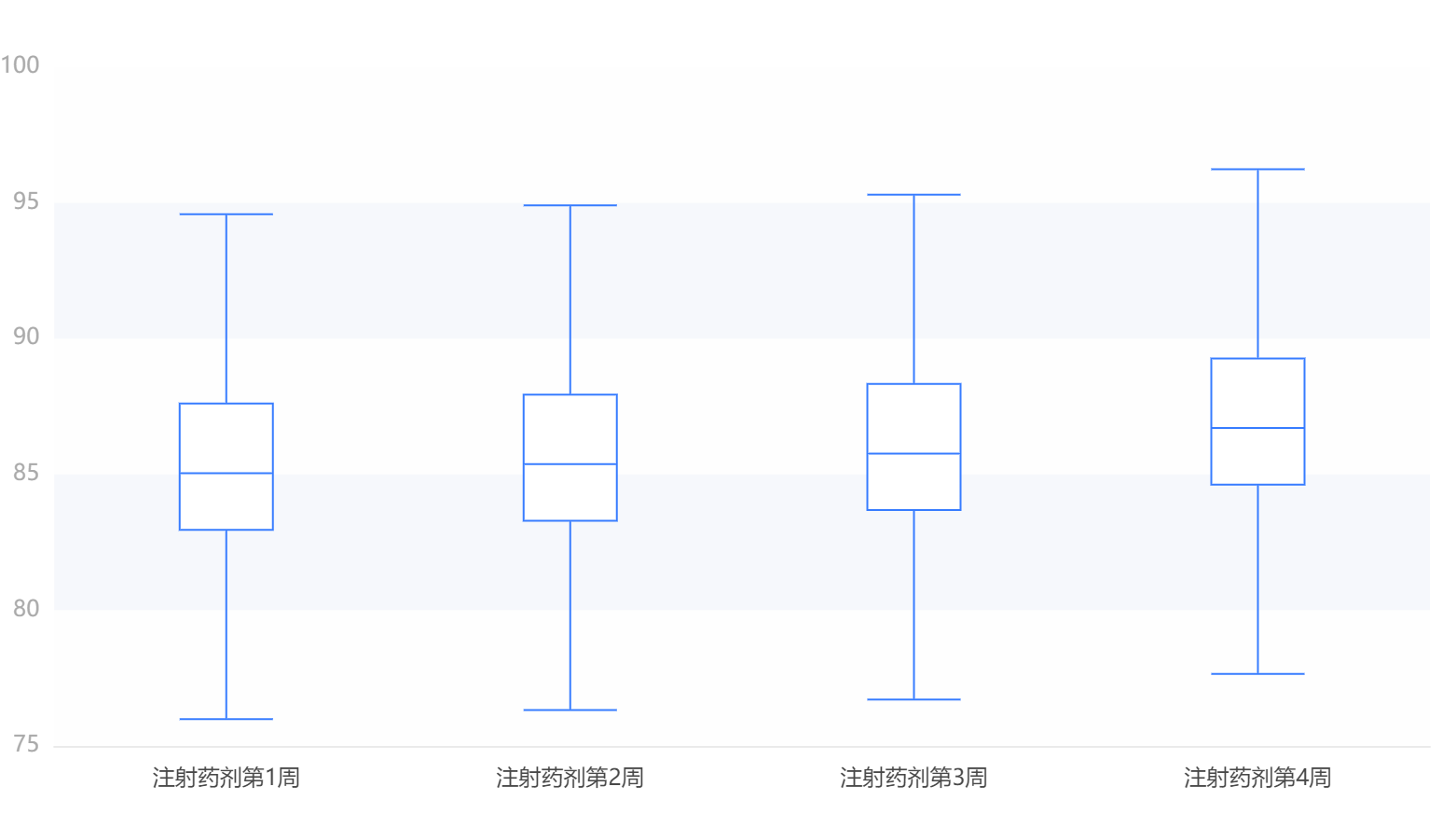

图表说明：箱线图是利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法，它也可以粗略地看出数据是否具有有对称性，分布的分散程度等信息，特别可以用于对几个样本的比较。
可见四个样本差异很小，且每周服药后的血压有提升的趋势。

输出结果 5：事后多重比较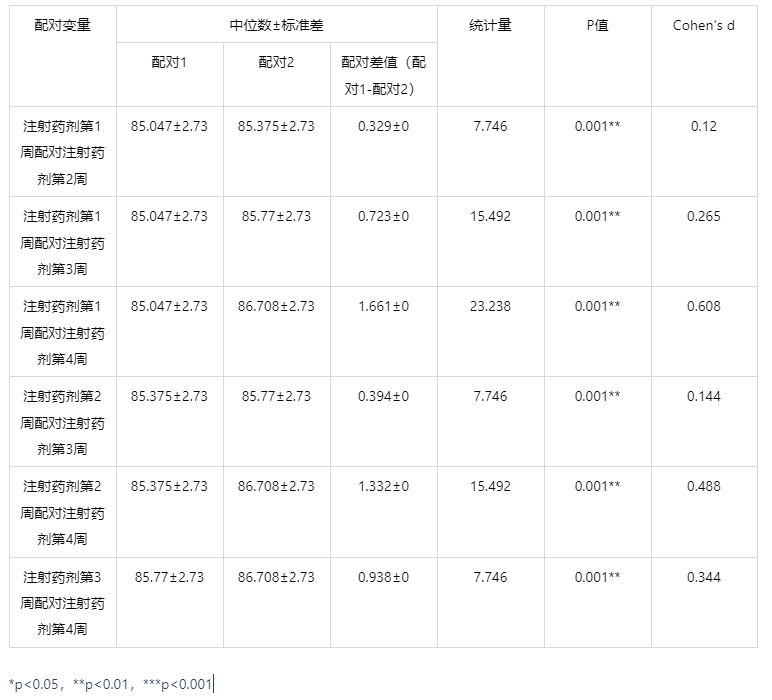

图表说明：
Friedman 检验只能判断各总体平均数间是否有差异，多重比较可用来进一步确定哪两个变量间有差异，哪两个变量间没有差异。
由于各周血压的 P 值均小于 0.01，故可以认为，每次注射了新药之后，血压都有差异性。从配对差值可以看出，差异性主要是上升，每次注射新药后，血压都会少量的上升。从 Cohen's d 值和配对差值可以看出，第三周到第四周的提升幅度是最大的。

# 7、注意事项

当需要比较多配对样本的差异情况时，如果发现数据呈非正态分布并无法转换为正态分布时，选择 Friedman，否则使用方差分析。
各差异性分析模型的使用场景如下总结：

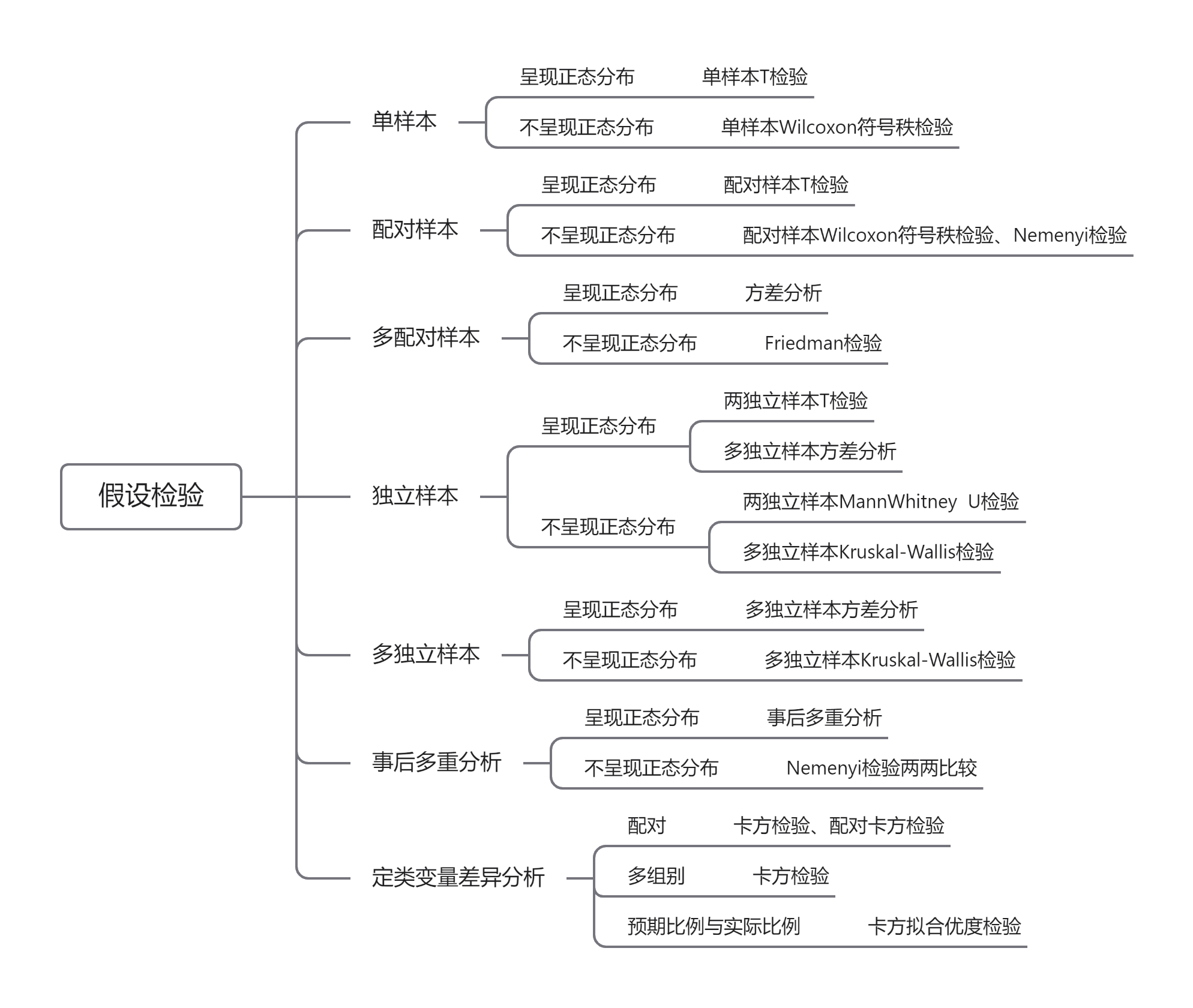
# 8、模型理论

假设有 k 个样本(处理)，b 个区组，记 θ1，θ2，…，θk 为其位置参数，则检验问题为:
H0:θ1=θ2=…= θk
H1:不是所有的 θi 都相等
由于区组的影响，要首先在每个区组中计算各个处理的秩，再把每个处理在各个区组中的秩相加。
记Ｒ ij 为第 j 个区组中 i 处理的秩，则秩按照处理而求得的和为：

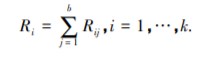
Friedman 统计量定义为:

对于有限的k和b，有零假设下的分布表可查，查表时要做变换：

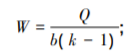
当查不到时，对于固定的k，当b→∞时，在零假设下有Friedman统计量Q→χ2(k－1)。

# 9、手推步骤

# Step 1：计算 $F r i e d m a n$ 统计量 $Q$

公式：

$Q = \frac{12}{b k (k + 1)} \sum_{i = 1}^{k} R_{i}^{2} - 3 b (k + 1)$

参数：

b = 100

（区组数），

k = 4

（处理数），

\sum R_{i}^{2} = 100^{2} + 200^{2} + 300^{2} + 400^{2} = 300, 000

代入计算：

$Q = \frac{12}{100 \times 4 \times 5} \times 300, 000 - 3 \times 100 \times 5 = \frac{12}{2000} \times 300, 000 - 1500 = 1800 - 1500 = 300$

# Step 2：显著性检验

自由度： $d f = k - 1 = 3$
卡方临界值（ $α = 0.05$ ）： $χ_{0.95}^{2} (3) = 7.815$
由于 $Q = 300 ≫ 7.815$ ，P值远小于0.001，拒绝 $H_{0}$ 。

# Step 3：效应量计算

结合公式和罗列数据，可得：

$f = \sqrt{\frac{Q}{b (k - 1)}} = 0.229$

# Step 4：事后多重比较（ $N e m e n y i$ 检验）

公式：

$z = \frac{R_{i} - R_{j}}{\sqrt{\frac{b k (k + 1)}{6}}} \approx 23.238$

对应P值远小于0.001，所有配对比较均显著。

# 10、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com. (opens new window)
[2]程晓亮.鞍山地区经济数据的非参数统计分析[J].鞍山师范学院学报,2017,19(04):6-8.

建议反馈