频谱分析

# 1、作用

频谱分析是信号处理中的重要技术，它可以帮助我们理解信号在频域上的特性。不同类型的谱（如功率谱、能量谱、相位谱、幅值谱）提供了不同方面的信息，有助于对信号进行更深入的分析和处理。

# 2、输入输出描述

输入：1个定量信号序列x。
输出：不同类型的谱信息。

# 3、案例示例

案例：假设我们有一个声音信号，我们想要分析该信号的频谱特性。

# 4、案例数据

# 5、案例操作

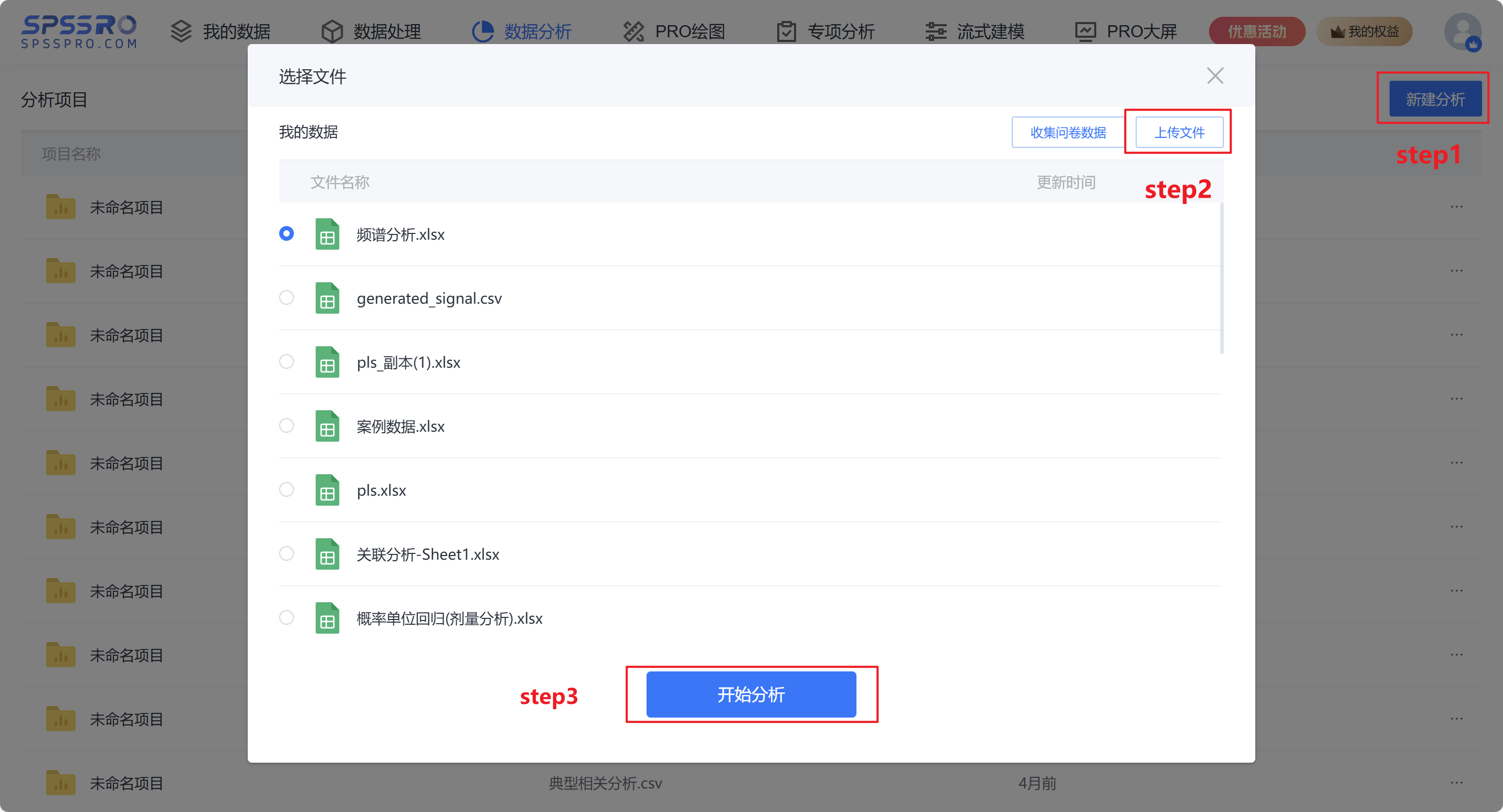
Step1：新建项目；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

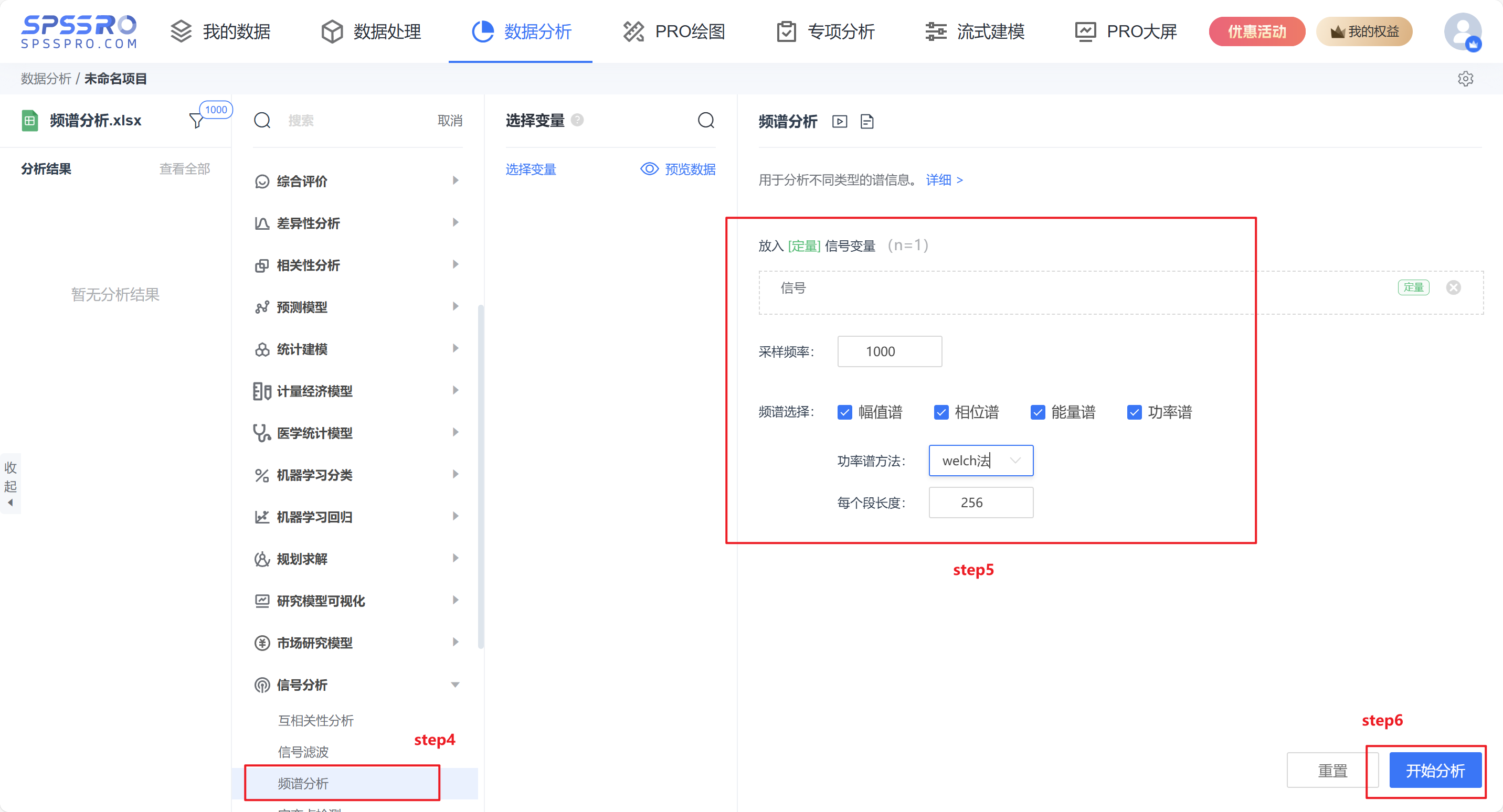
step4：选择【突变点检测】；
step5：选择突变点检测的方法；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

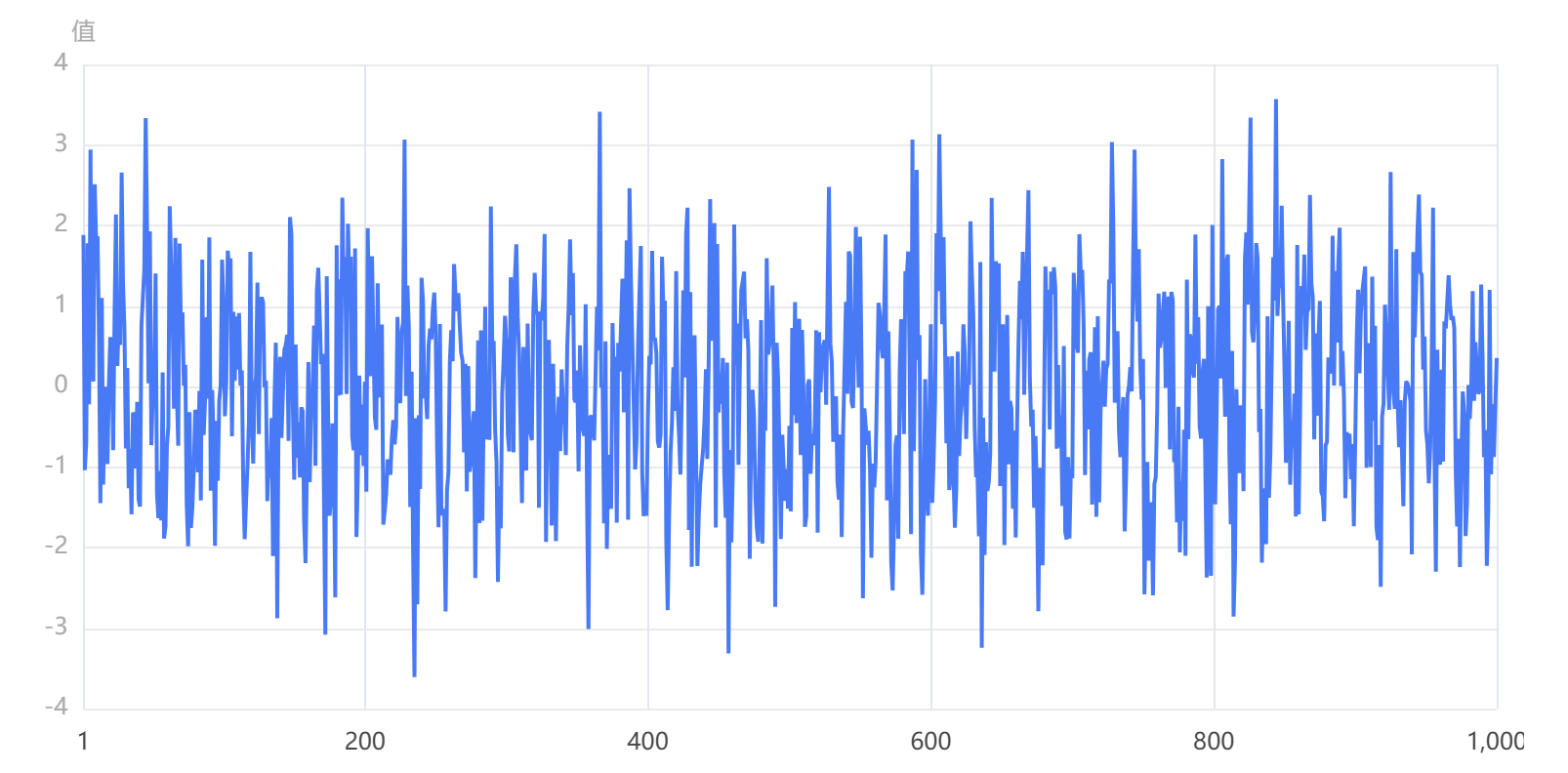
输出结果1：时域谱

输出结果2：幅值谱

输出结果3：相位谱

输出结果4：能量谱

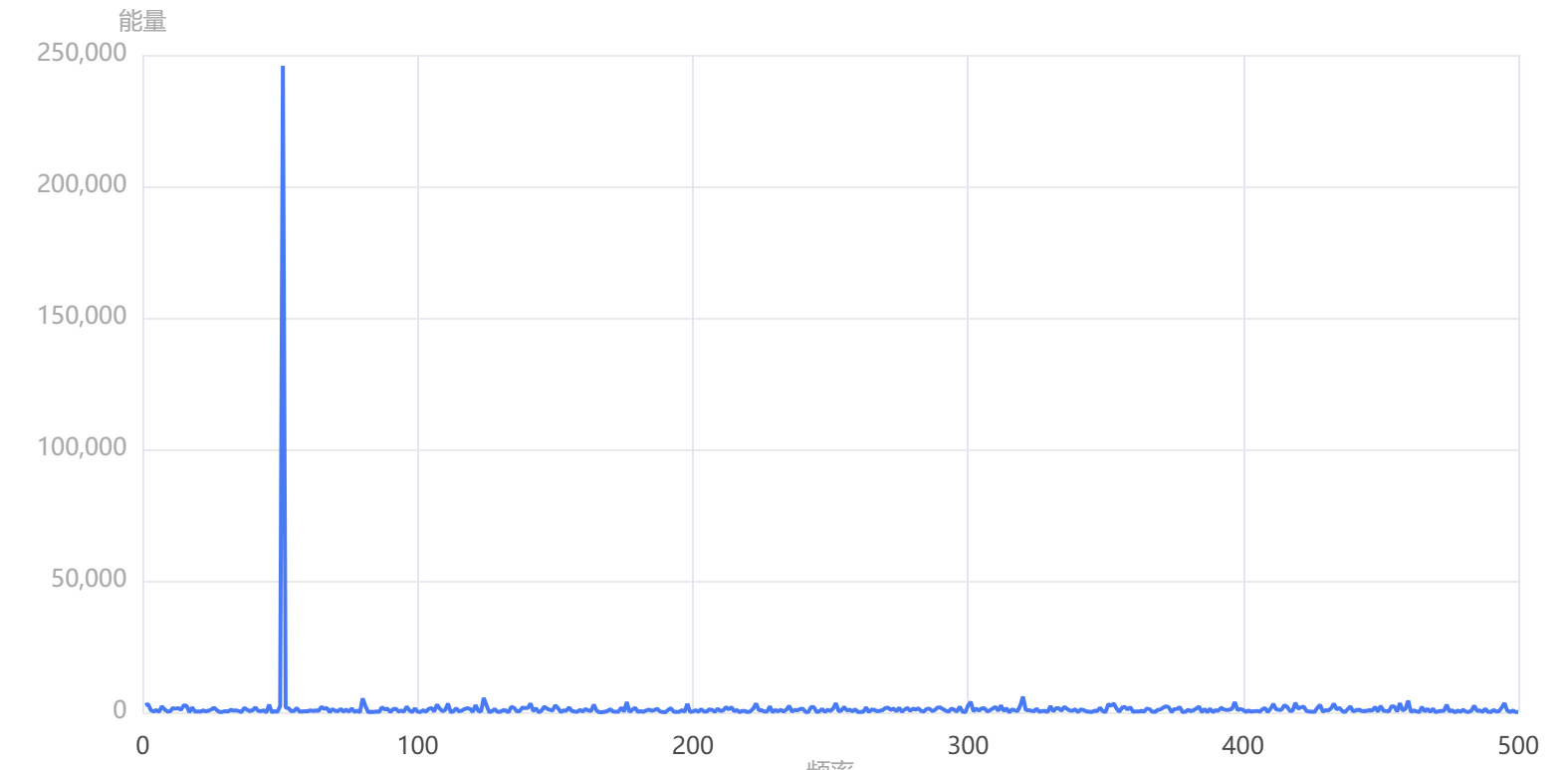
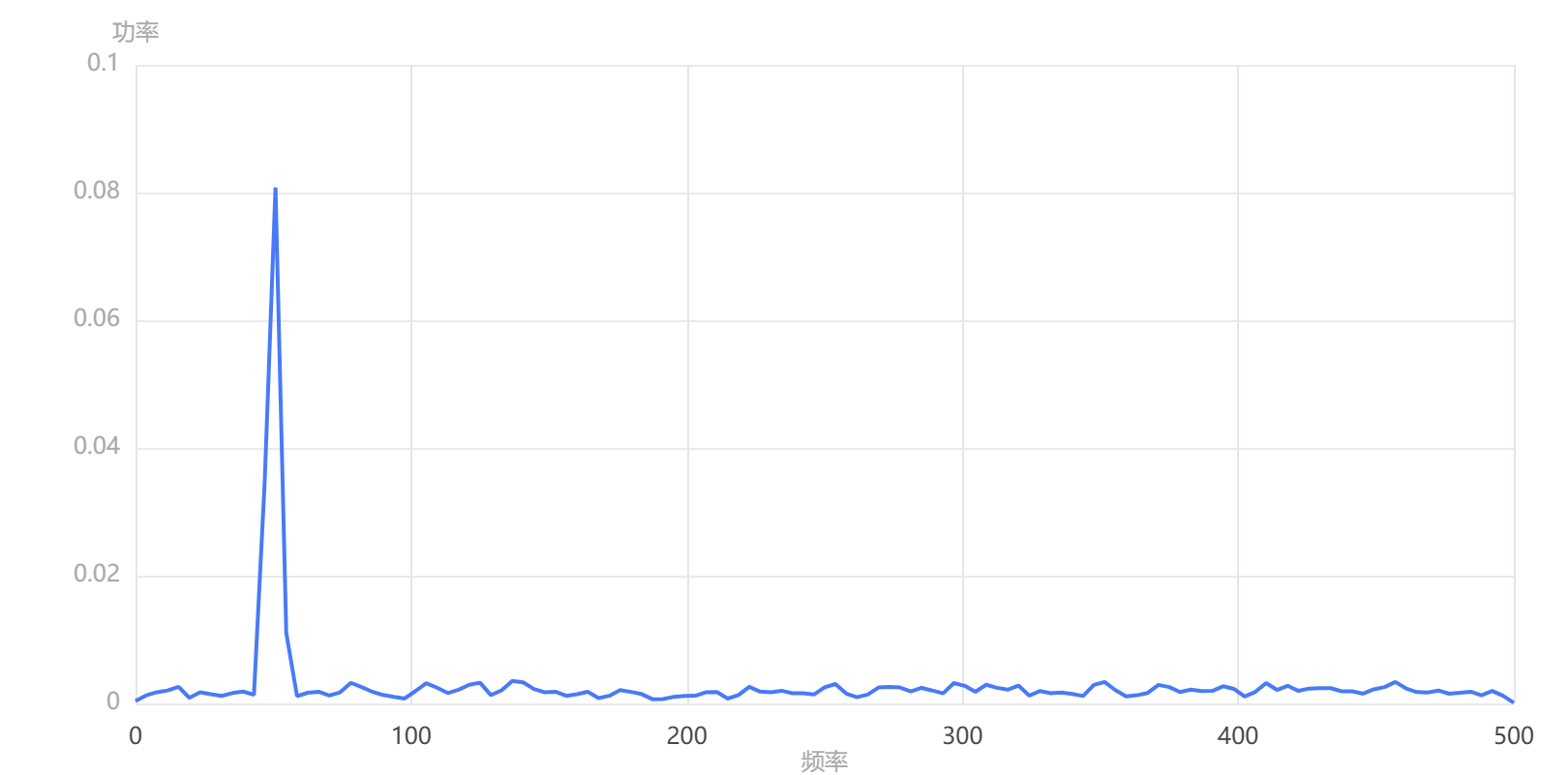
输出结果5：功率谱

# 7、注意事项

采样频率指的是在单位时间内采样的次数。 平台要求的采样频率以赫兹（Hz）作为单位 ，它表示每秒钟从连续信号中采集多少个样本。

# 8、模型理论

（1）幅值谱
幅值谱表示信号在不同频率上的幅度，反映了信号的频率成分强度。

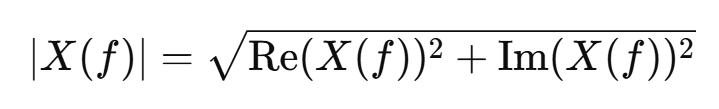
其中，X(f)信号的傅里叶变换结果，Re和Im分别表示实部和虚部。

（2）相位谱
相位谱描述信号各频率成分的相位信息，表明波形的位移和时延。

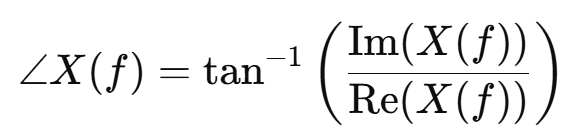
相位谱提供了信号各频率成分的相位信息。

（3）能量谱
能量谱描述信号在频域的能量分布，适用于有限能量的信号。

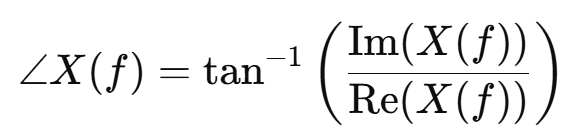
能量谱是幅值谱的平方，表示每个频率成分的能量。

（4）功率谱
功率谱可以揭示信号在不同频率上所含的功率信息，用于找出信号的主导频率成分。 下列展示几种计算方法；周期图法、自相关法、welch法；
（4.1）周期图法
周期图法是一种最直接的频谱估计方法，通过对信号进行快速傅里叶变换（FFT）来计算频谱。计算步骤：

• 计算信号的傅里叶变换（DFT）。
• 对傅里叶变换的结果取模平方，得到功率谱。
• 将结果归一化（通常除以信号长度 N）。

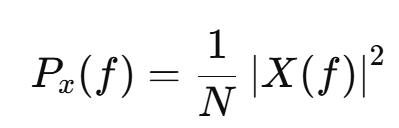
（4.2）welch法
Welch 方法是一种改进的周期图法，通过对信号进行分段、加窗和平均来提高谱估计的平滑性。Welch 方法将信号划分为多个重叠的片段，对每一段使用窗函数处理，求其功率谱，然后将这些分段谱进行平均，以降低估计方差。

• 将信号分成 K段，每段长度为 N_w，通常使用 50% 重叠。
• 对每一段信号加窗（如汉宁窗、汉明窗）。
• 计算每段的 DFT，然后取模平方，得到每段的功率谱。
• 对所有段的功率谱进行平均，得到最终的功率谱。

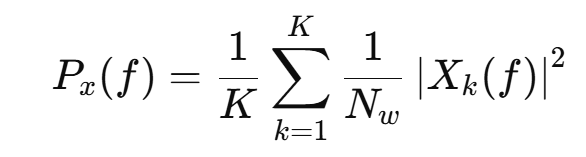
（4.3）自相关法
自相关法基于维纳-辛钦定理，通过信号的自相关函数的傅里叶变换来估计功率谱密度。维纳-辛钦定理表明，信号的功率谱密度等于信号自相关函数的傅里叶变换。

• 计算信号的自相关函数 Rx[m]。
  
• 对自相关函数计算傅里叶变换，得到功率谱。

在功率谱分析中，通常关注的不是绝对的数值大小，而是找到峰值频率、低频或高频成分， 可以相对比较不同频率成分的强弱，但更重要的是相对变化而非绝对值。通过强度的变化趋势可以跟踪信号特征的变化（如设备故障）。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.