信号滤波

# 1、作用

信号滤波用于去除噪声、抑制干扰、增强信号质量，以提高信号传输的可靠性和性能，从而为数据分析、系统控制、诊断判断等提供支持。

# 2、输入输出描述

输入：1个定量信号序列x。 输出：滤波后的数据。

# 3、案例示例

案例：假设我们有一个声音信号，我们希望去除噪声并保留声音信号的主要部分。

# 4、案例数据

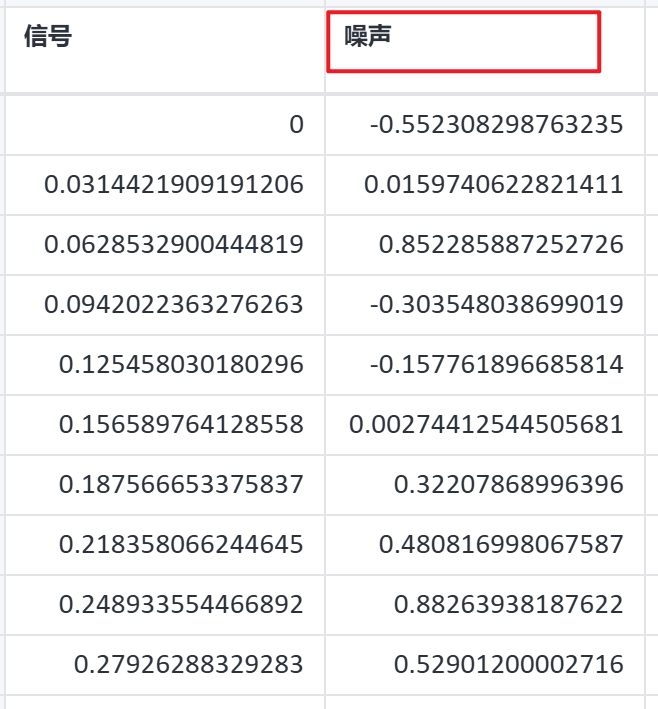
# 5、案例操作

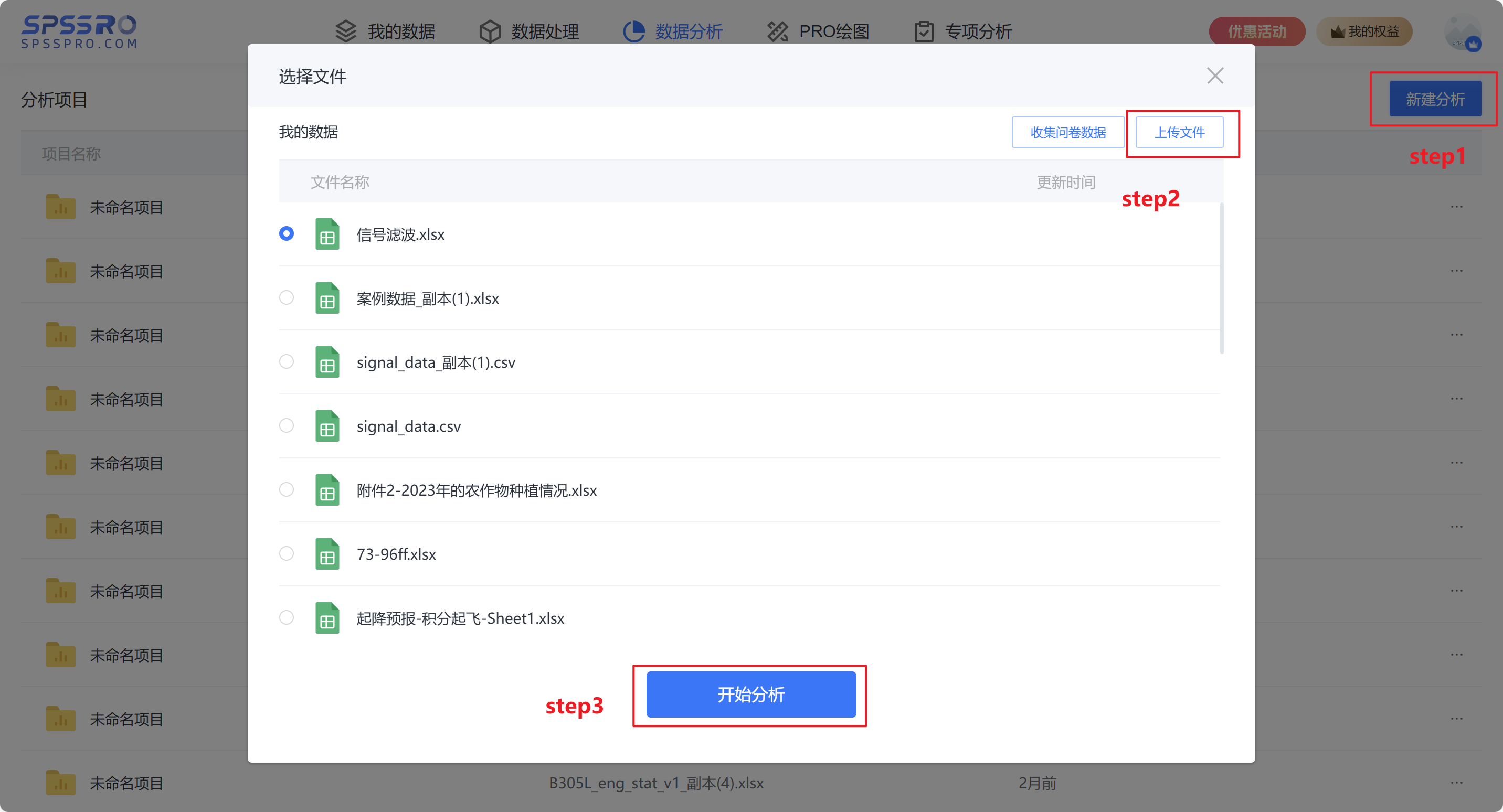
Step1：新建项目；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；
step4：选择【信号滤波】；
step5：选择滤波方法相关参数，并确定是否需要生成滤波后的信号；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：原信号与滤波后信号对比图

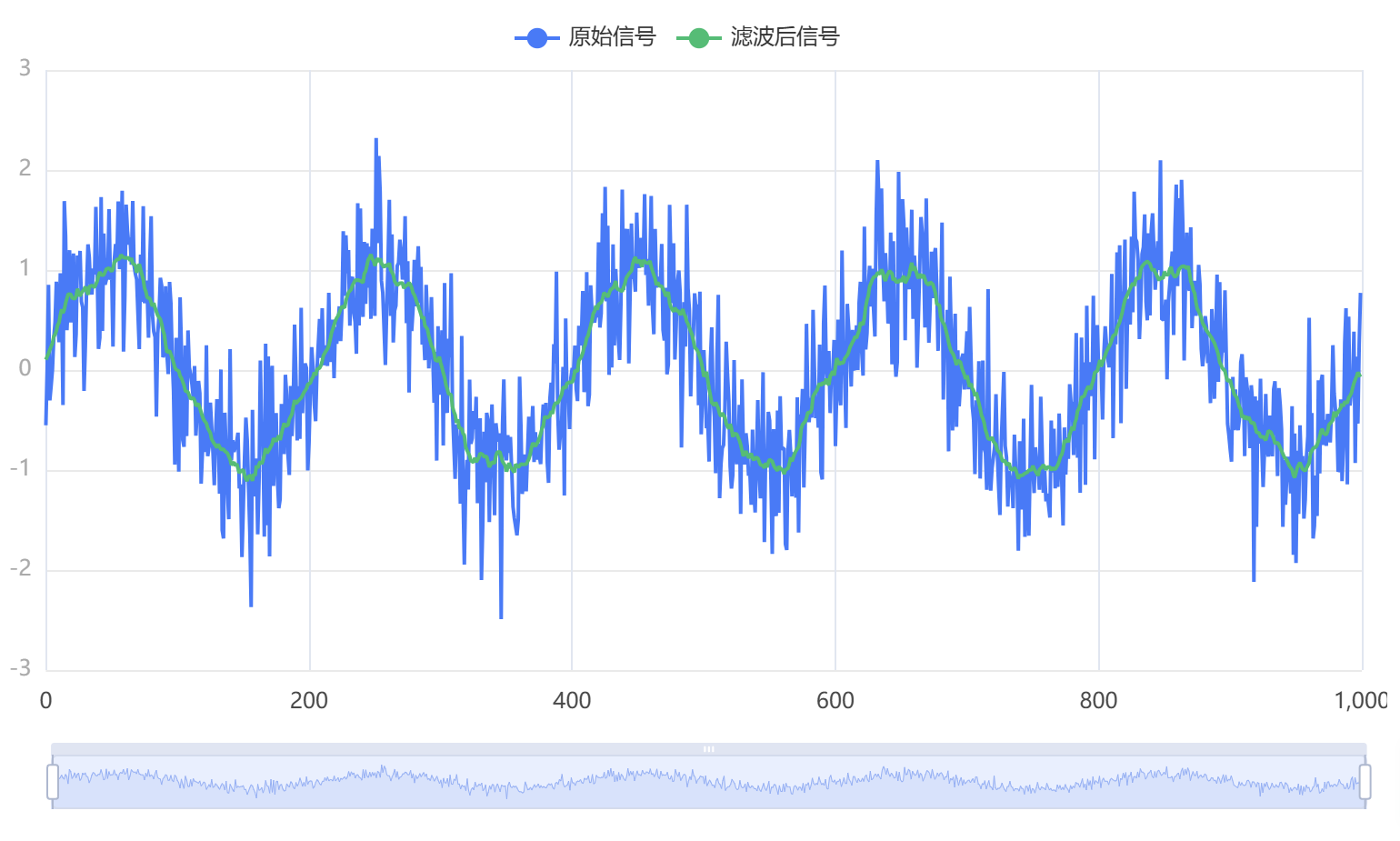
图表说明：上图是原信号和滤波后的信号对比图，通过对比图，可以清晰地看到滤波后信号相对于原始信号的变化。

# 7、注意事项

• 协变量应是定量变量。
• 各处理组协变量的均值最好差别不要太大，否则最终修正所依赖的协变量总体均值会在各处理组的x范围外，就算是各处理组的回归外推，可能会不准确。

# 8、模型理论

信号滤波包含三种方法：滑动滤波、维纳滤波、和巴特沃斯滤波

（1） 滑动滤波
滑动滤波器是一种简单的时域滤波方法，通过对输入信号在滑动窗口内的值求平均来平滑信号。它是最常见的低通滤波器之一，特别适用于去除高频噪声。假设窗口大小为 N，则输出 y(n)是从 x(n)到 x(n−N+1)的平均值：

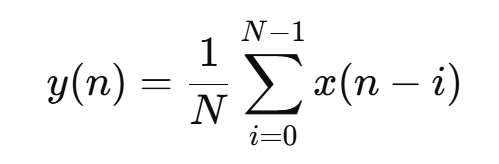
（2） 维纳滤波
维纳滤波是一种基于最小均方误差准则的统计滤波器，主要用于去除信号中的噪声，同时尽可能保留信号的有用成分。 假设有一组已知的信号和噪声的先验统计特性（如均值和方差），维纳滤波通过这些信息来找到最优滤波器，以最小化噪声对信号的影响。在实际应用中，尤其是图像处理和时间序列处理场景，信号和噪声的特性往往是局部变化的，因此需要在局部窗口内动态估计这些特性。

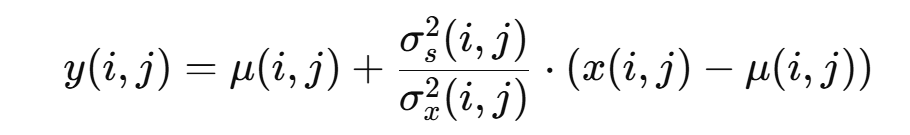
• x(i,j) 是带有噪声的输入信号 ；
• y(i,j) 是滤波后的信号值；
• μ(i,j)是窗口内的局部均值，即窗口内所有像素或数据点的平均值；
• [σ_x(i,j)]²是窗口内的局部方差，即信号与噪声的总体方差， 反映了输入信号（带噪声）的总体波动性 ;
• [σ_s(i,j)]²是信号的局部方差，即去除噪声后的纯信号在局部窗口内的波动情况 ;

（3） 巴特沃斯滤波
巴特沃斯滤波器广泛应用于噪声抑制。通过在适当的频率范围内去除高频或低频噪声，滤波器能够有效地清理信号。 可以通俗地理解为一种信号过滤工具，主要用于清理噪声或隔离频率成分，以使信号更加清晰和有用。它就像是一个“筛子”，只允许特定频率范围的信号通过，阻止不需要的频率成分。
低通滤波器：允许低频信号通过，而阻止高频信号通过。这种滤波器通常用于去除信号中的高频噪音或者使信号变得更加平滑。
● 高通滤波器：允许高频信号通过，而阻止低频信号通过。这种滤波器通常用于去除信号中的低频噪音或者突出高频成分。
● 带通滤波器：只允许特定频率范围内的信号通过，而阻止其他频率的信号通过。这种滤波器通常用于提取特定频率范围内的信号或者滤除特定频率范围外的噪音。
● 带阻滤波器：阻止特定频率范围内的信号通过，而允许其他频率的信号通过。这种滤波器通常用于去除特定频率范围内的干扰或噪音。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.