互相关性分析

# 1、作用

用于分析待分析信号在不同超前量或滞后量下与基准信号的皮尔逊相关性。可以识别出两个信号之间最强的关联性出现在哪个时间偏移处。这对于理解事件的因果关系、预测或系统动态响应等方面是非常有用的。

# 2、输入输出描述

输入：1个定量基准信号序列，1个定量待比较信号序列。
输出：待分析信号在不同超前量或滞后量下与基准信号的皮尔逊相关系数。

# 3、案例示例

案例：环境学家想要研究城市交通流量对空气质量的影响。具体来说，想要了解道路上车辆数量的增加是否会导致附近空气中污染物（比如二氧化氮NO₂）浓度的增加。因此，监测一个交通繁忙的路口的车流量和该区域的空气质量，得到数据后进行互相关性分析。

# 4、案例数据

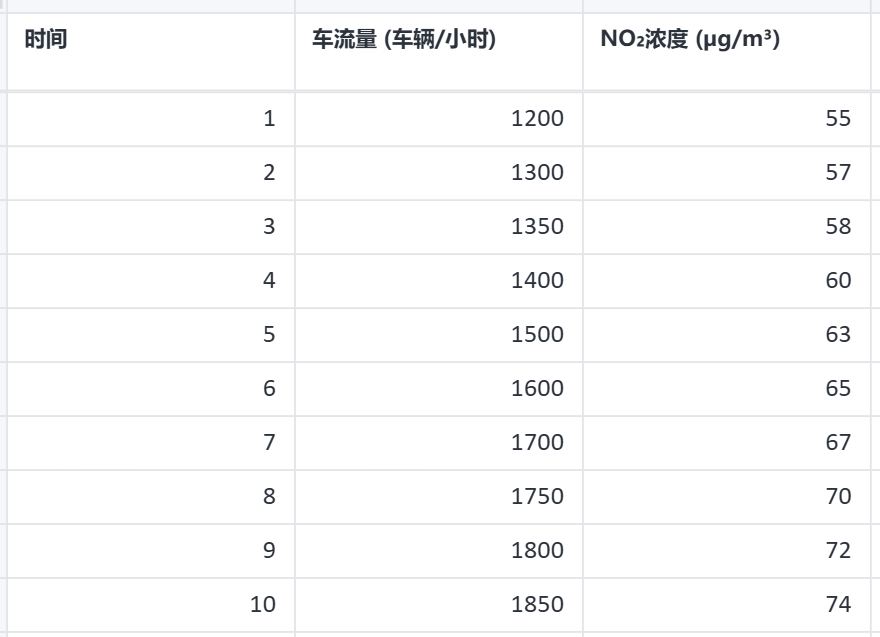
# 5、案例操作

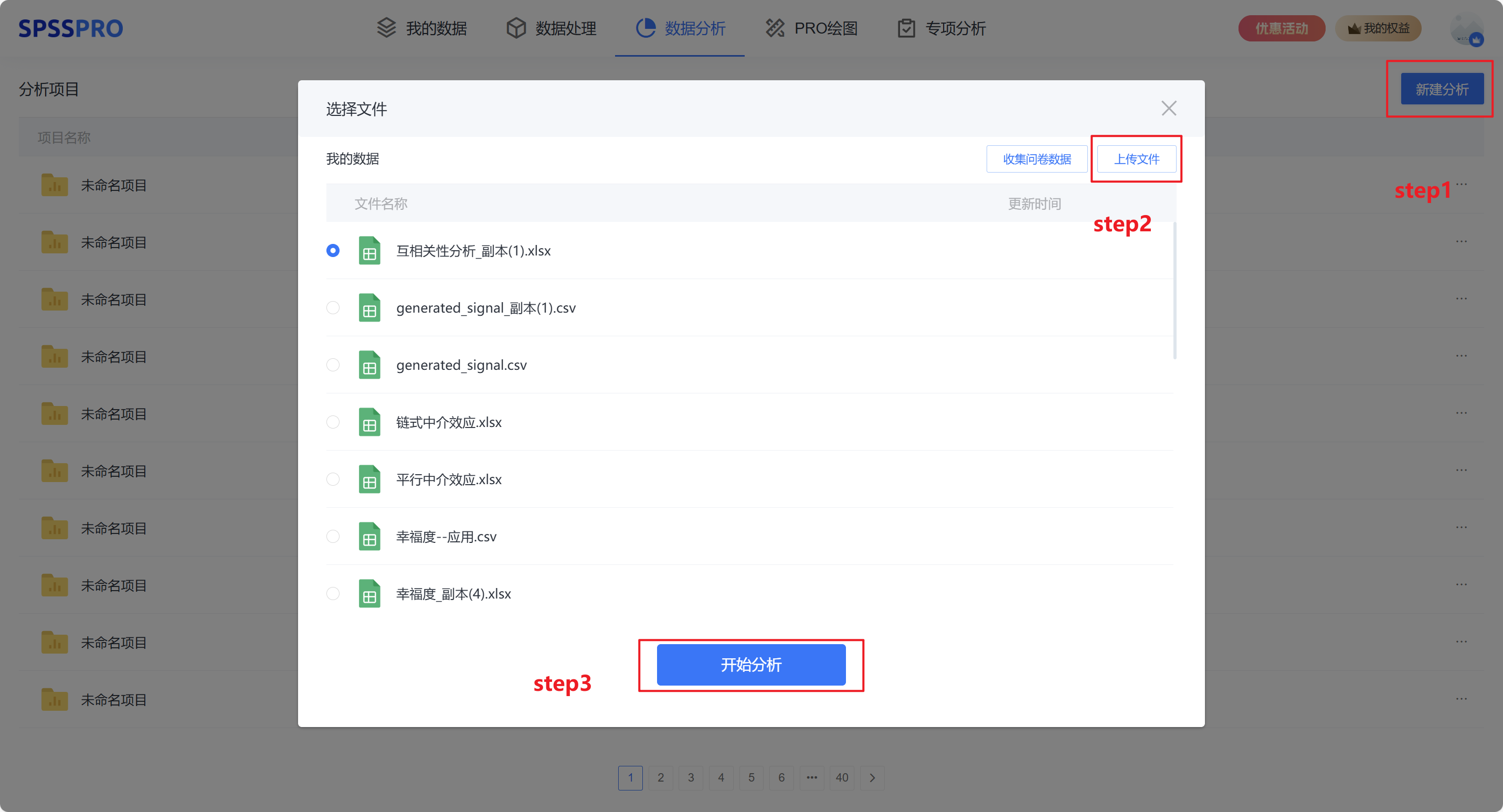
Step1：新建项目；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

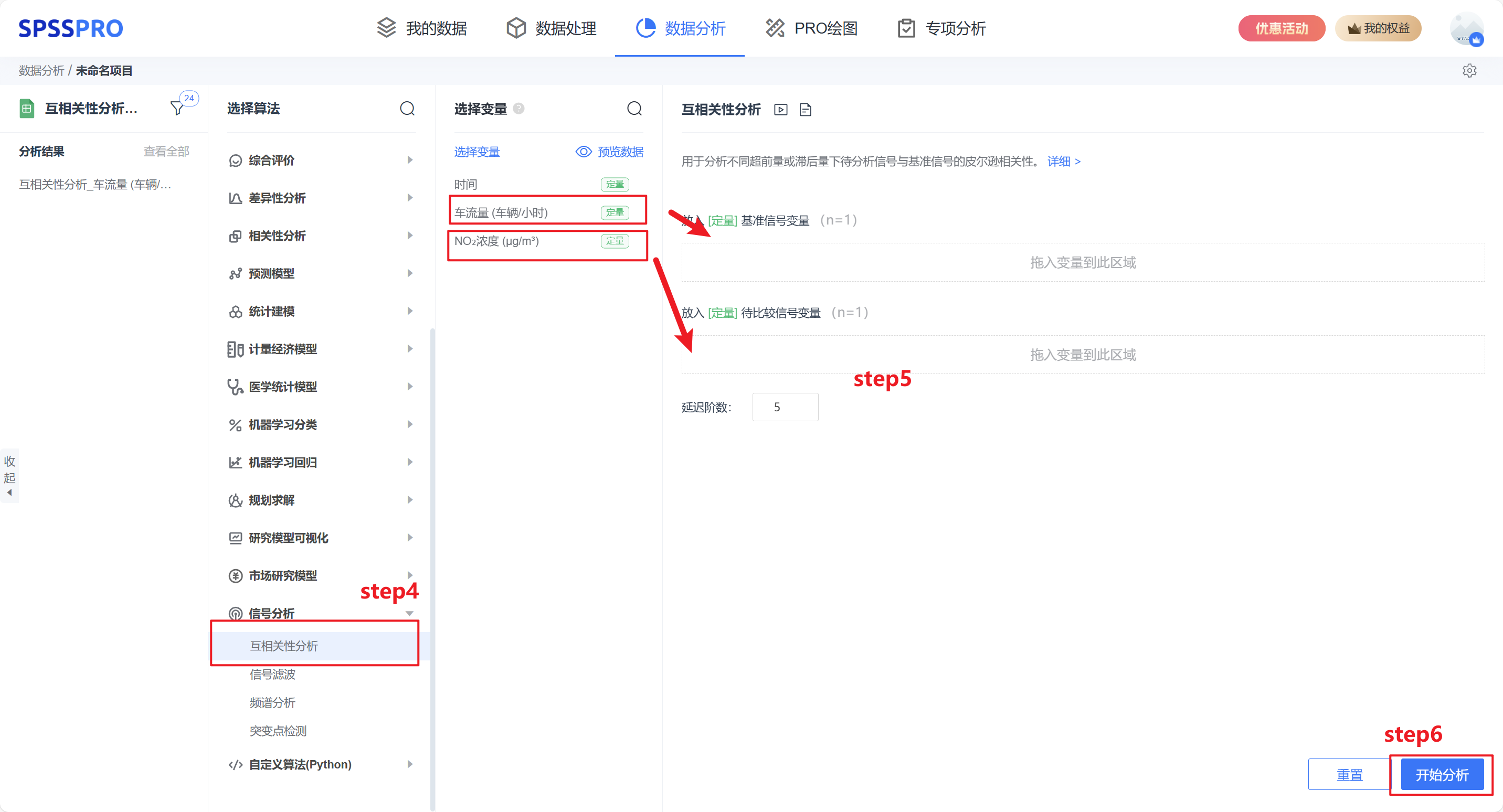
step4：选择【互相关性分析】；
step5：选择互相关性分析的延迟阶数；

• 延迟阶数为0：表示信号是同步的，即两个信号在相同时间点上进行比较。
  
• 延迟阶数为正数：表示后续信号（例如NO₂浓度）受前续信号（如车流量）的影响。
  
• 延迟阶数为负数：表示前续信号（如车流量）受后续信号（NO₂浓度）的影响。
  

step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：基准信号-变量1趋势图

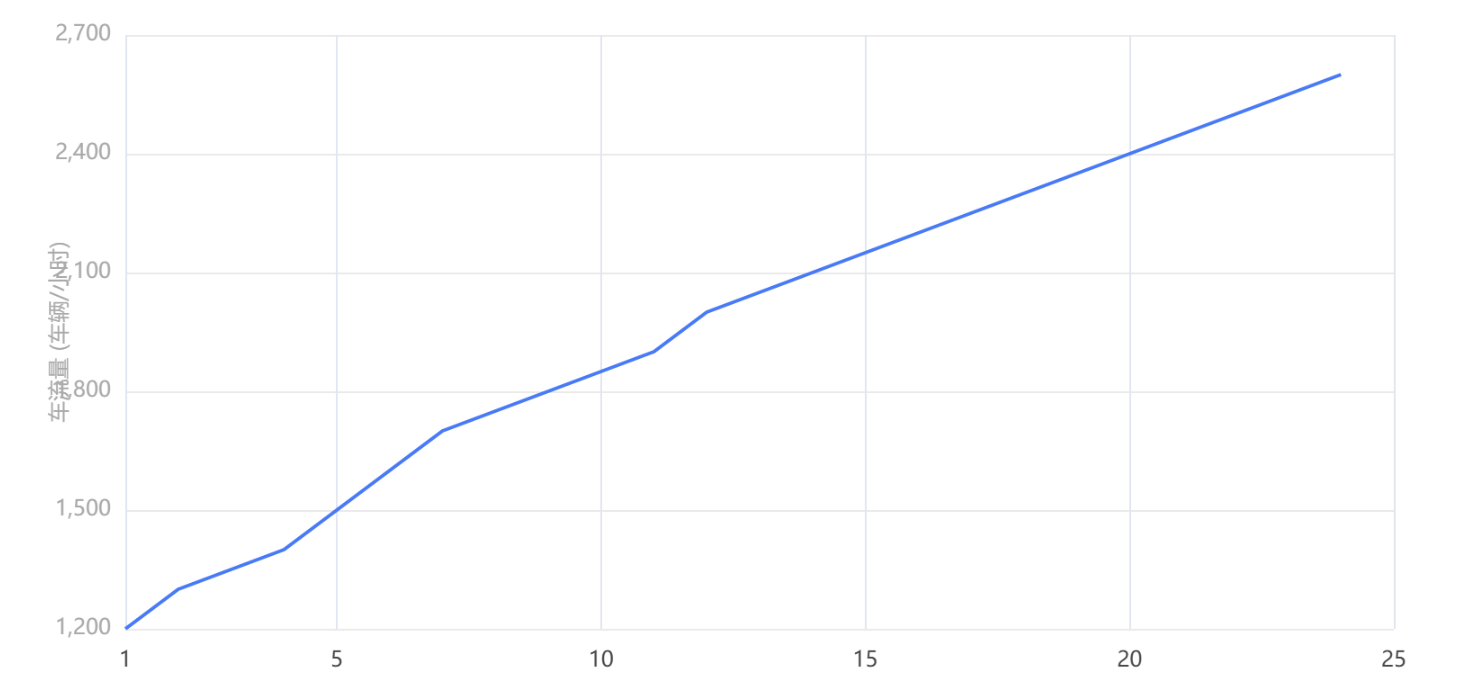
图表说明：上图展现了变量1的趋势图

输出结果2：待比较信号-变量2趋势图

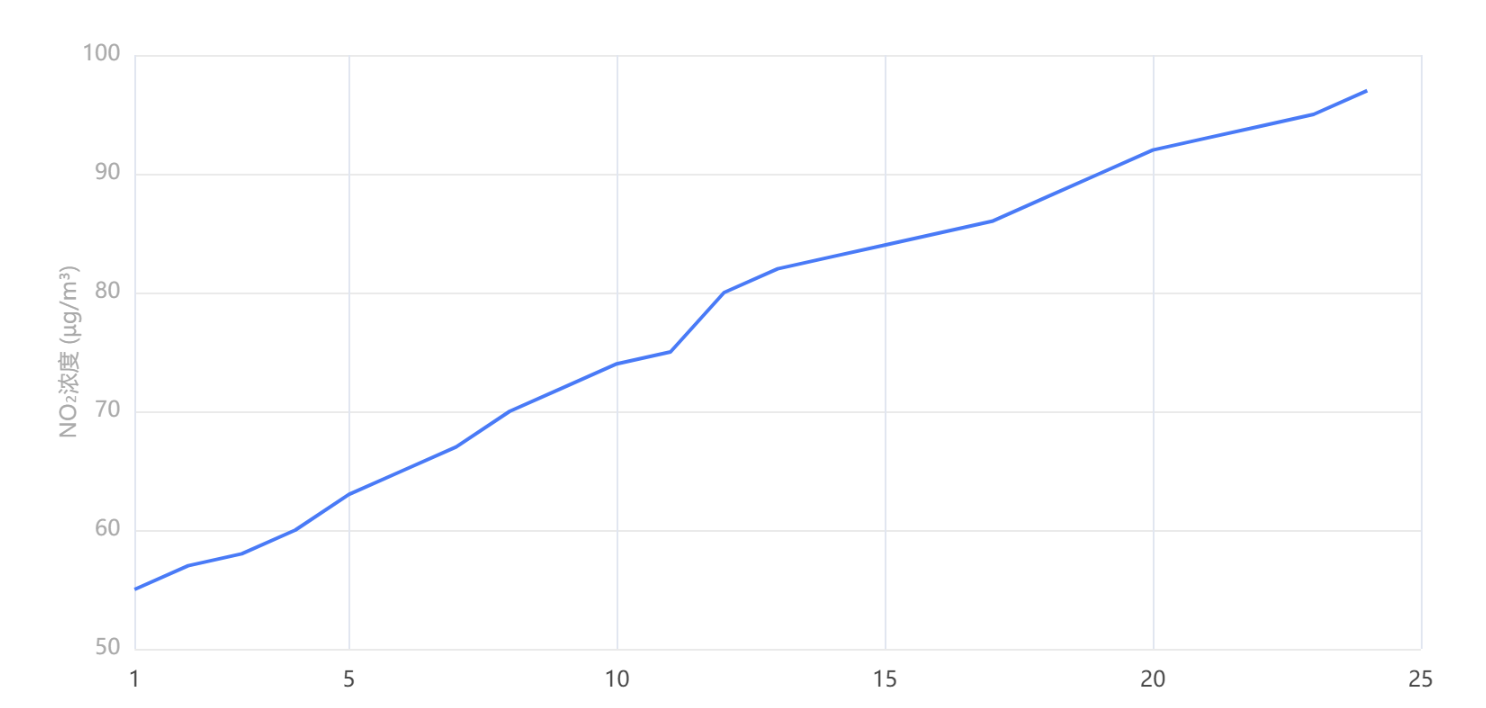
图表说明：上图展现了变量2的趋势图

输出结果3：互相关性分析图

图表说明：上图展示了待分析信号在不同超前量（X 负半轴）或滞后量（X周正半轴）下与基准信号 的 Pearson 相关系数。

● X轴表示滞后量，负值表示待分析信号相对于基准信号是超前的，正值表示它是滞后的。例如，-5表示待分析信号比基准信号提前5个时间单位，而+5表示待分析信号比基准信号延后5个时间单位；
● Y轴表示皮尔逊相关系数的值，值越接近+1，表示在对应的滞后量下，两个信号之间正相关性越强；
● 相关系数接近 0 表明两个信号之间没有线性关系；
● 如果最高的相关系数发生在正滞后处，这意味着待分析信号落后于基准信号；
● 如果最高的相关系数发生在负滞后处，这意味着待分析信号领先于基准信号。

具体的分析结论可以从以下几个方面来进行：

• 即时影响强度**：找到相关性最高的位置，如果在延迟为0时的相关性最高，表明车流量的变化会立即影响NO₂浓度，支持了车辆排放对空气污染物浓度的直接贡献。**
• 持续性影响**：在较大延迟（如5小时）下依然有较高的相关性，可能说明车流量的影响存在持续性，即污染物浓度会随着车流量的增加而持续在空气中残留。这可能与气象条件（如风速、温度）或地形有关。**

# 7、注意事项

在计算互相关性分析时，靠近边界的数据（开始和结束部分）没有足够的前后信息 ，所以延迟阶数不能特别大，一般延迟范围选择为总样本数的10%-20%以内比较合理 ，否则可能会导致计算的互相关结果不准确 ；

# 8、模型理论

互相关分析是一种用于评估两个信号之间相似性和时间偏移的统计工具。它通过计算一个信号在不同时间偏移下与另一个信号的相关性，帮助识别它们之间的关联性及其强度，此处的关联性是使用pearson相关1系数；

通过计算不同时间偏移下的互相关函数，可以识别：信号之间最强的关联性出现在哪个时间偏移处、事件之间的因果关系、系统的动态响应特性。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.