分位数回归

# 1、作用

分位数回归既能研究在不同分位点处自变量 X 对于因变量 Y 的影响变化趋势，也能研究在不同分位点处的哪些自变量 X 是主要影响因素。原理是将数据按因变量进行拆分成多个分位数点，研究不同分位点情况下时的回归影响关系情况。

# 2、输入输出描述

输入：自变量 X 至少一项或以上的定量变量或二分类定类变量，因变量 Y 要求为定量变量。
输出：自变量在不同分位点处的显著性及自变量系数在不同分位点的变化趋势。

# 3、案例示例

案例：建立分位数回归来分析产品质量、广告投放对产品销售的影响。

# 4、案例数据

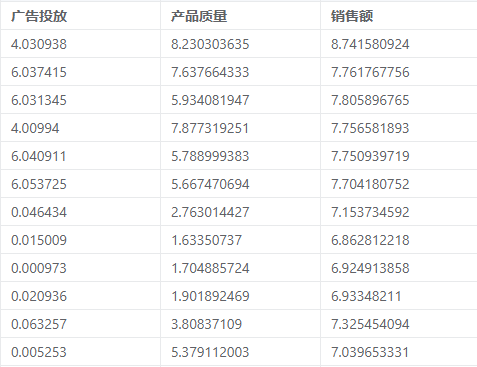
# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；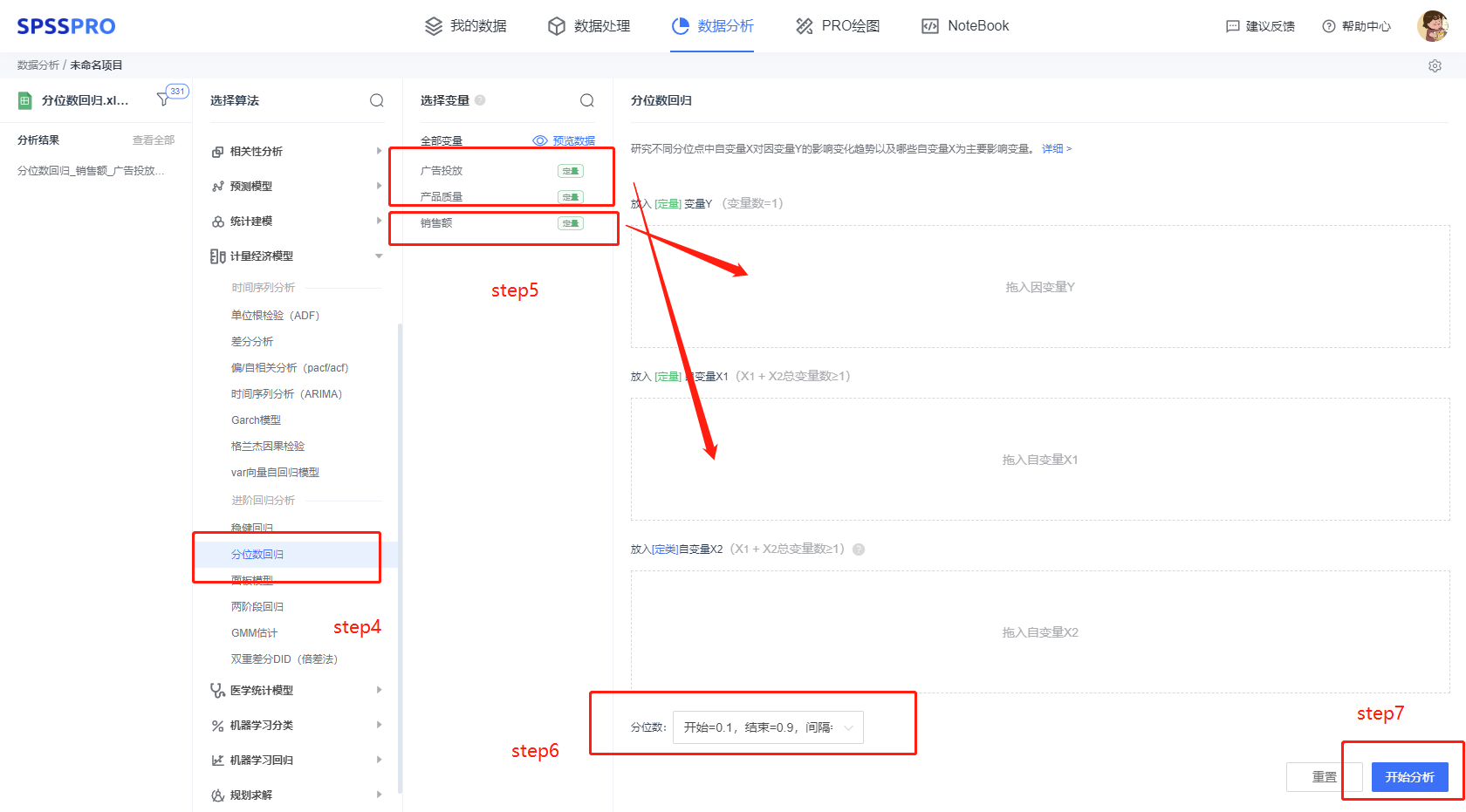

step4：选择【分位数回归】；
step5：查看对应的数据数据格式，按要求输入【分位数回归】的数据。
step6：选择分位数。
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：分位数回归结果表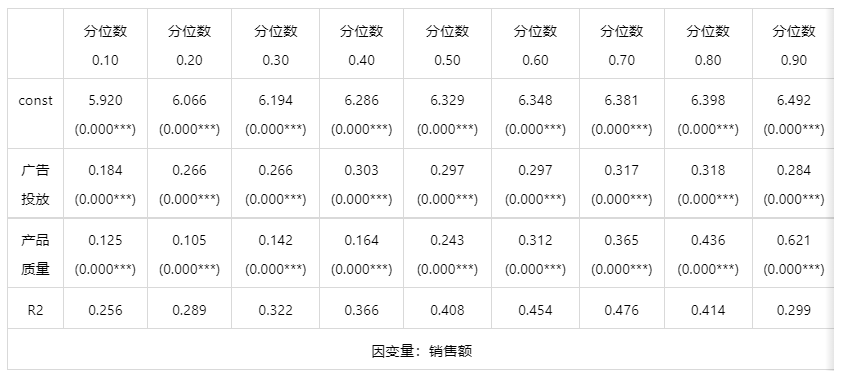

图表说明：上表格展示了分位数回归的参数结果，包括分位数点、变量、样本量、拟合度 R² 等，可从两方面来进行分析：
● 在不同分位数处自变量对因变量的回归系数呈现的变化趋势。横向来看表格，比如，对于产品质量，它的回归系数随着分位数的增大而不断增大，这说明随着产品质量的不断提高，对产品销售的影响逐渐增大。
● 在不同分位数处各个自变量的显著性。纵向来看表格，对于某个分位点，如 0.5 分位点，两个自变量的系数都是显著的（p 值小于 0.05），说明广告投放和产品质量都对销售额有影响。

输出结果 2：分位数回归系数及其置信区间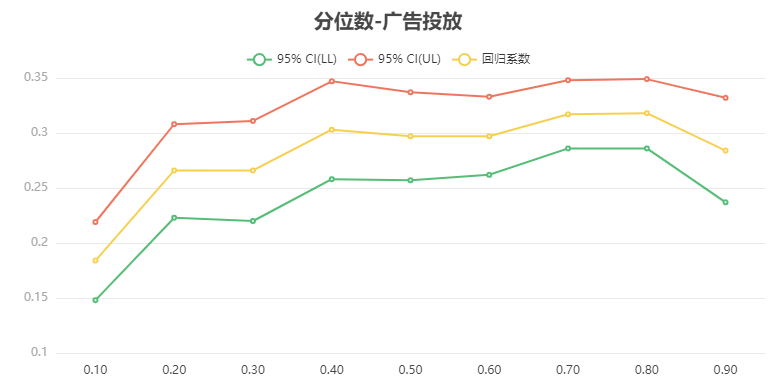

图表说明：上图展示了分位数回归的参数结果，可以对每个变量的分位数回归图进行影响幅度分析。对于变量-广告投放，从分位数 0.2 起，广告投放对产品销售来说有明显的提升，并且从分位数 0.2-分位数 0.9 过程中，广告投放对产品销售的影响较为平稳。由此我们可以得到结论，广告投放资源的 0.2 分位点处就能得到对销售有利的影响，且在 0.4 分位点就能达到最高影响销售的力度，没必要花到最大的广告投放资源。

图表说明：上图展示了分位数回归的参数结果，可以对每个变量的分位数回归图进行影响幅度分析。对于变量-产品质量，分位点的回归系数整体上是逐渐增加的，并且在 0.9 分位点处对销售的影响是最高的，这说明随着产品质量的不断提高，对产品销售的影响逐渐增大。

# 7、注意事项

• 若样本量太小，会存在部分分位数回归系数的 p 值为 NaN，此时需增大样本量。

# 8、模型理论

普通线性回归模型关注的是均值，研究的是在某些解释变量在取值固定的条件下响应变量的期望均值，模型估计方法是最小二乘法，使各个样本残差平方和(MSE)最小。

分位数回归提出的原因，就是因为不希望仅仅是研究 y 的期望，而是希望能探索 y 的完整分布状况，或者说可能在某些情况下我们更希望了解 y 的某个分位数。进一步的我们可以画出不同的分位数回归曲线，这样才能能更加明显地反映出，随着 x 的增大，y 的不同范围的数据是不同程度地变化的，而这个结论通过以前的回归分析是无法得到的，这就是分位数回归的作用。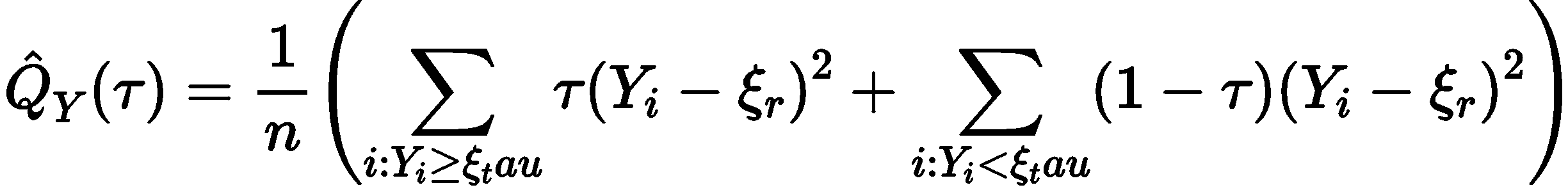

本质上，分位数回归就是一个加权最小二乘法（虽然形式上有点不一样），给不同的 y 值（大于分位点和小于分位点的 y）不同的权重，比如现在我们有一个数据集是 1 到 10 各整数，我们希望求 0.7 分位数，假设这个 0.7 分位数是 q，然后所有大于 q 的数都被赋上权重 0.7，小于 q 的赋予权重 0.3。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] koenker R，Bassett GW．Regression quantiles[J]．Econometrica，1978，46：33-50．