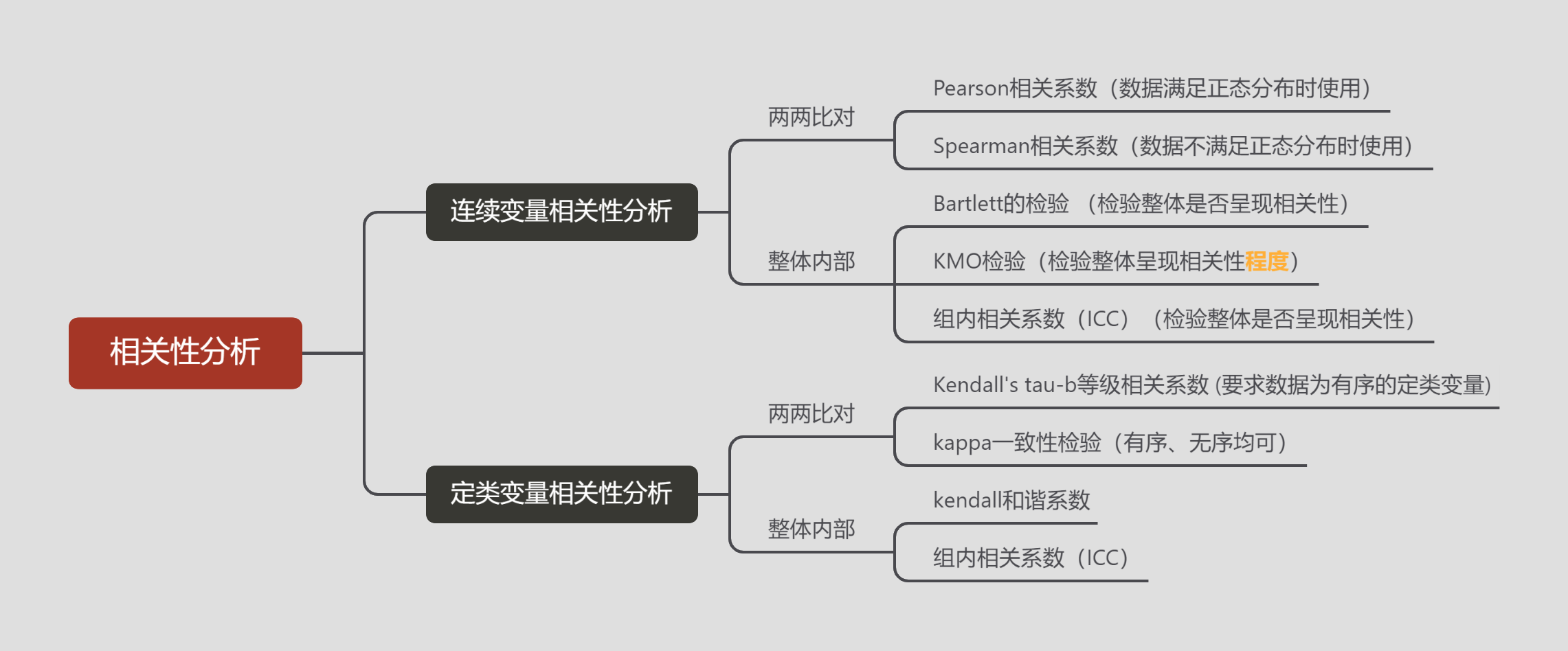
Kendall一致性检验

# 1、作用

肯德尔（Kendall）系数用于定类数据的相关性检验，与此类似的有 Kappa 系数一致性检验。这两者不同的是：Kappa 系数与皮尔逊一样是比较两项之间的相关性；而 Kendall 系数用于判断总体（全部数据）的相关性，适用于数据是多列相关的等级资料，即可是 k 个评分者评(N)个对象，也可以是同一个人先后 k 次评 N 个对象。通过求得 kendall 和谐系数，可以较为客观地选择好的作品或好的评分者。
​

# 2、输入输出描述

输入：三组以上定类变量。
输出：整体的一致性程度。

# 3、案例示例

分析 10 个旅游评论家对 5 个景点的打分一致性程度。
​

# 4、案例数据

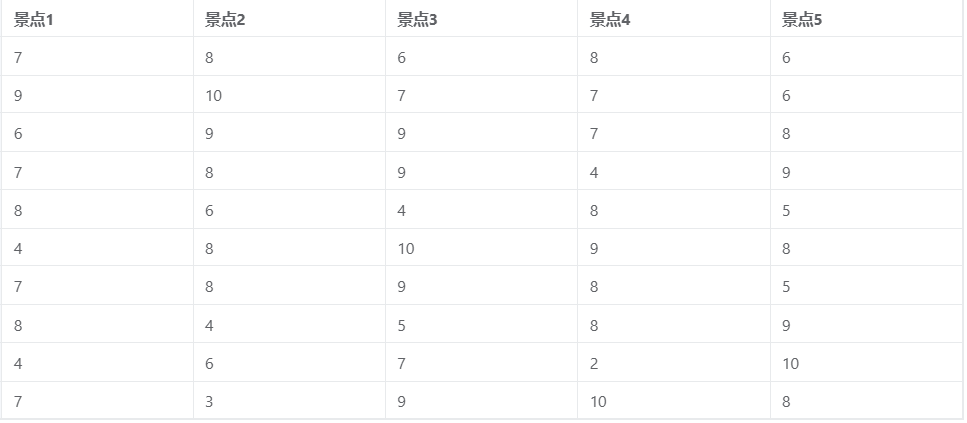
Kendall 协调系数案例

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；


step4：选择【Kendall 协调系数】；
step5：查看对应的数据数据格式，【Kendall 协调系数】要求输入变量为至少两项或以上的定量变量或者有序定类变量。
step6：点击【开始分析】，完成全部操作。
​

# 6、输出结果分析

输出结果：Kendall 一致性检验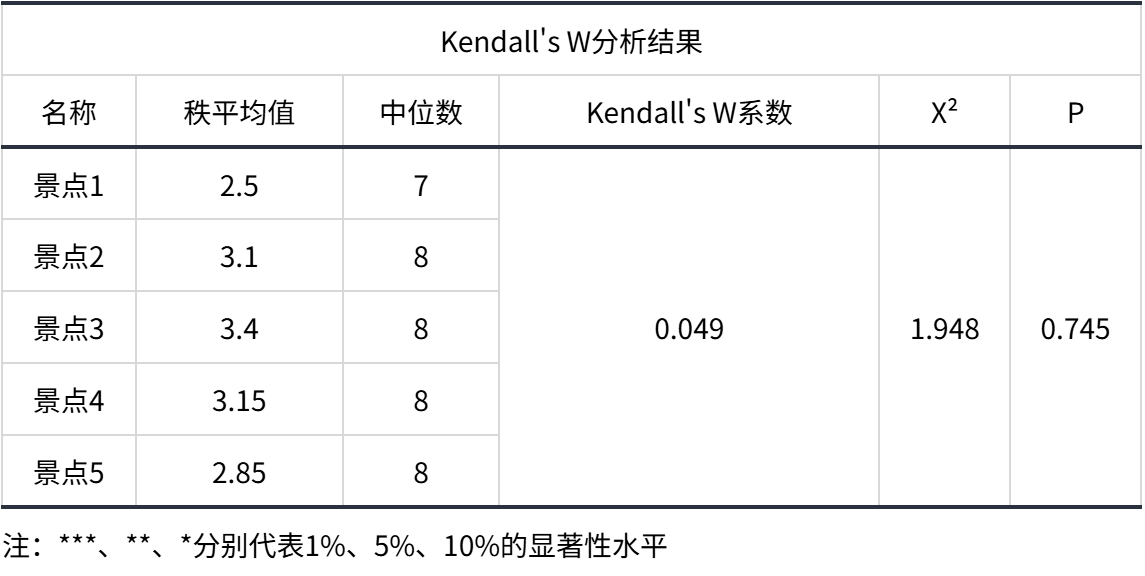

图表说明：
上表展示了模型检验的结果，包括：秩平均值、中位数、Kendall 协调系数 𝑊、卡方值、显著性 𝑝 值；
Kendall系数一致性检验的结果显示，总体数据的显著性P值为0.745，水平上不呈现显著性，不能拒绝原假设，因此数据不能呈现一致性，同时模型的Kendall协调系数𝑊值为0.049，因此相关性的程度为极低的一致性。可见五位评委对景点的评分不具有一致性。

# 7、注意事项

• Kendall 协调系数与其他分析的区别为：
  
  

# 8、模型理论

Kendall’s W 检验, 即肯德尔和谐性分析, W 统计量称和谐性系数或一致性系数 ( coefficient of concordance) , 用于度量一致性好坏。常用于考察多位评分者评分的一致性程度。对同一份数据作分析, Kendall’s W 检验拒绝 H0 与否和 Friedman 检验完全相同, 但它们所检验的 H0 不相同 , Kendall’s W 是 Friedman 统计量正态化的结果, 取值在 0~1 之间, 用以度量不同测量之间的一致性, 系数越接近 1。一致性越高。计算公式如下:

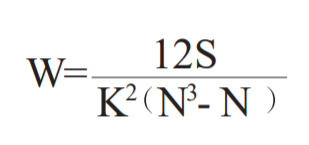
式中,S 为秩和与其平均值之差的平方和,K 为秩评定的组数,N 为被评秩的对象数。
用卡方检验,构造统计量 χ2=K(N-1)rw,其中自由度为 N-1。
判断准则:
如果 χ2< χ2 (df)α, 那么有 100(1- α)%的把握可以断定 K 个变量总体不存在相关。
如果 χ2≥χ2 (df)α,那么有 100(1-α)%的把握可以断定 K 个变量总体存在相关。
​

# 9、手推步骤

# Step 1：数据秩次转换和计算平均值 $\overline{R}$

所有评委的秩次分配后，各景点的总秩和 $R_j$ 如下：

景点1：35；景点2：29；景点3：26；景点4：28.5；景点5：31.5

$\overline{R}=\frac{\sum R_j}{N}=\frac{35+29+26+28.5+31.5}{5}=30$

# Step 2：计算平方和 $S$

计算如下：

$S=\sum (R_j-\overline{R}{)}^2=(35-30{)}^2+(29-30{)}^2+(26-30{)}^2+(28.5-30{)}^2+(31.5-30{)}^2=49$

# Step 3. 计算Kendall协调系数 $W$

计算如下：

$W=\frac{12S}{K^2(N^3-N)}=\frac{12\times 49}{{10}^2\times (5^3-5)}=\frac{588}{12,000}\approx 0.049$

# Step 4:计算卡方统计量 ${\chi }^2$

计算如下：

${\chi }^2=K(N-1)W=10\times 4\times 0.049=1.948$

# Step 5:显著性检验

• 自由度 $df=N-1=4$
• 查卡方分布表，临界值 ${\chi }_{0.05}^2(4)=9.488$
• 由于 ${\chi }^2=1.948<9.488$，不拒绝原假设，$P$ 值 > 0.05。

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]李娟生,李江红,刘小宁,申希平,米友军.Kendall’s W 分析方法在医学数据处理中的应用及在 SPSS 中的实现方法[J].现代预防医学,2008(01):33+42.