Kappa一致性检验

# 1、作用

Kappa 系数用于定类数据的相关性检验，定量数据的相关性检验为皮尔逊相关系数。一般 Kappa 系数可用于衡量分类精度，或者投票等定类数据。
​

# 2、输入输出描述

输入：两个或以上的定类变量或有序定类变量，若为 Flesis Kappa，则为三组以上的定类变量或有序定类变量。
输出：两两变量之间是否呈现显著性相似以及相似的程度，若为 Flesis Kappa，则为变量整体的一致性程度。

# 3、案例示例

问卷调查一个班级的两个体育老师对学生体育锻炼的态度（分为：从不、偶尔、经常）划分情况，需要检验是否存在一致性。
​

# 4、案例数据

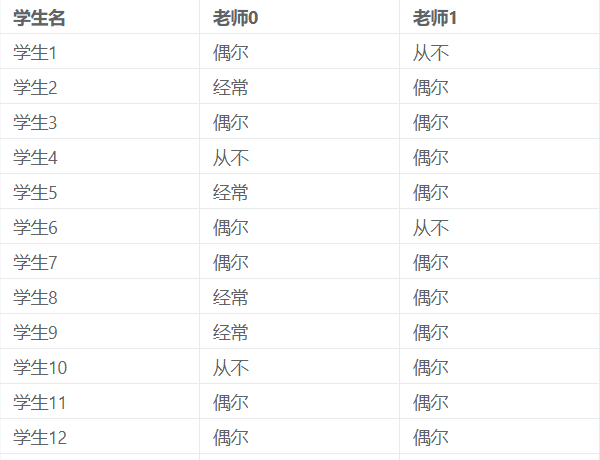
Kappa一致性检验

# 5、案例操作

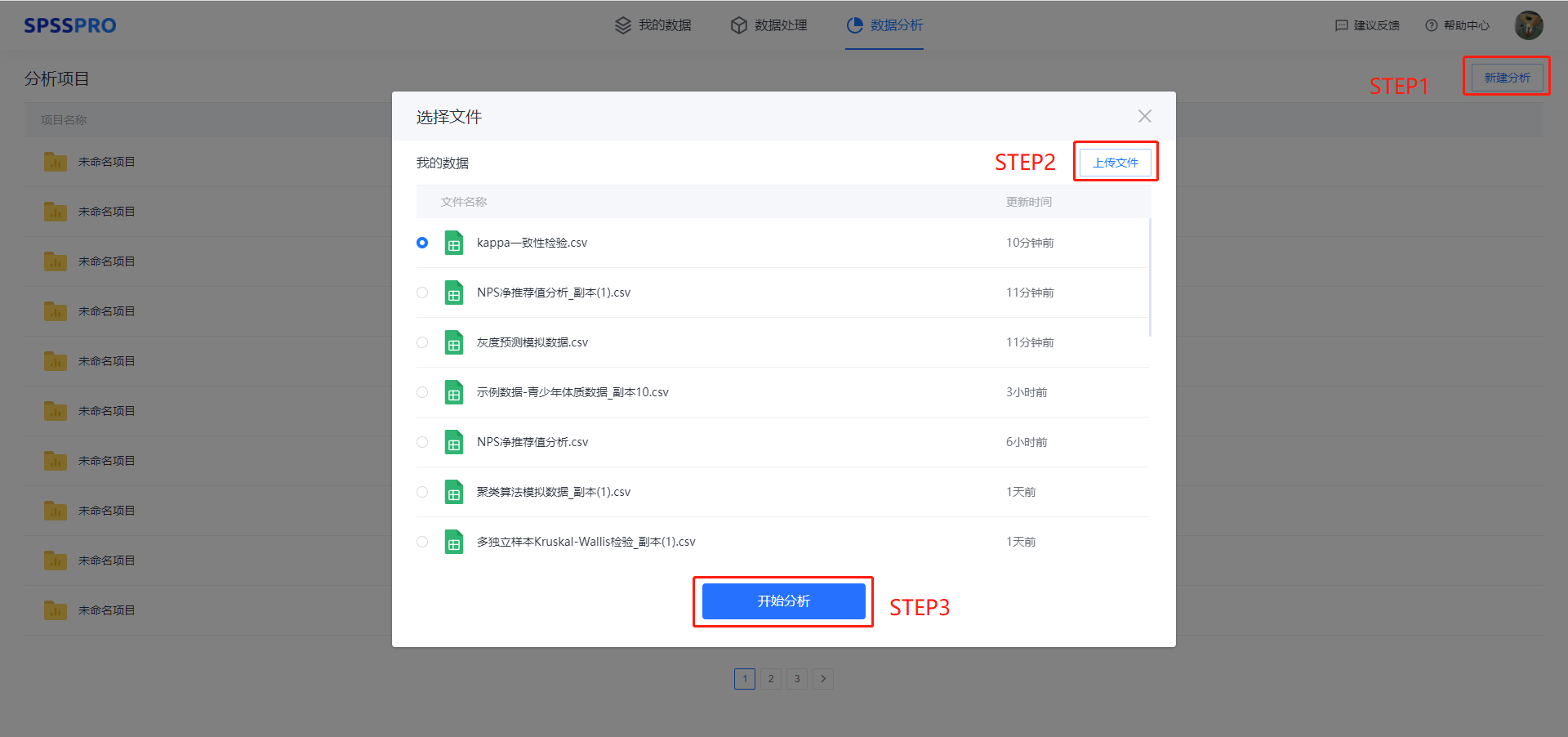
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；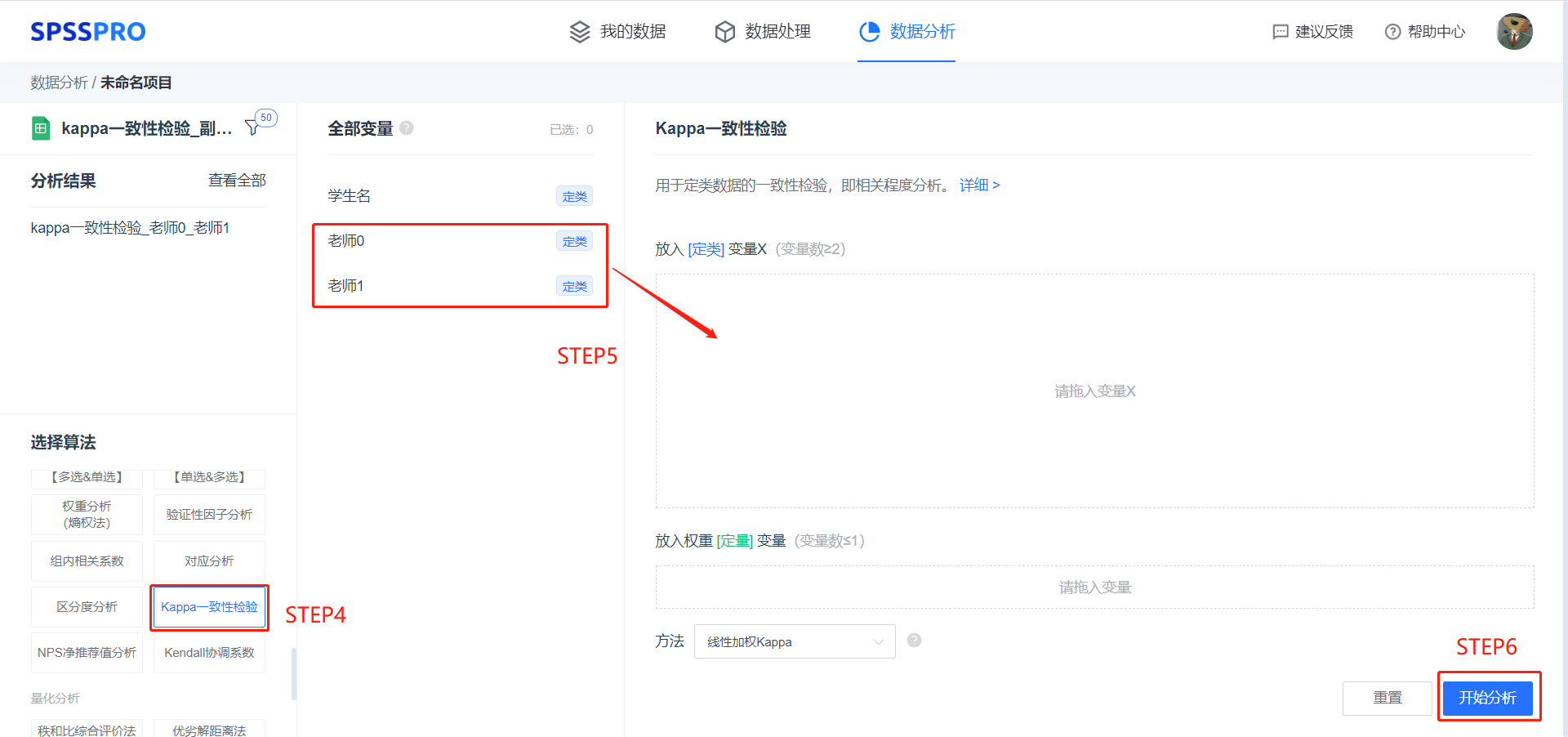

step4：选择【Kappa 一致性检验】；
step5：查看对应的数据数据格式，【Kappa 一致性检验】要求输入变量为至少两项或以上的定类变量,
如果是数据有序(不同结果会有不同的后果)则还要选择方法(故选择线性加权 KAPPA)，将定量变量拖入。
如果数据存在权重（如：已经分类汇总）则需要拖入定量变量。
step7：点击【开始分析】，完成全部操作

# 6、输出结果分析

输出结果 1：Kappa 一致性检验

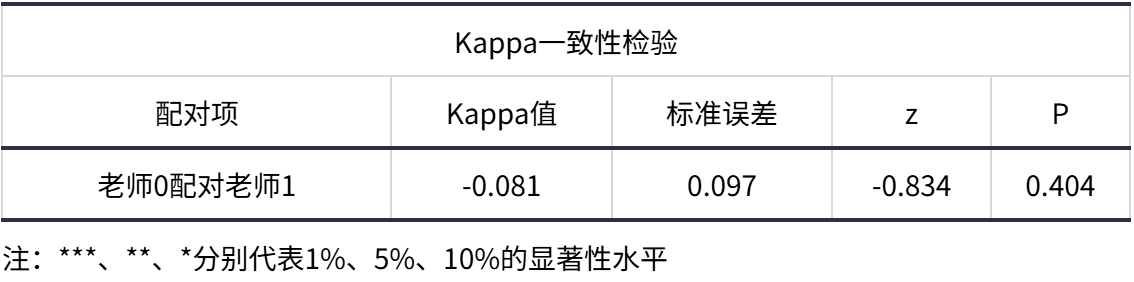
图表说明：
上表展示了Kappa系数检验的参数结果表，包括了Kappa系数、显著性P值。
1）先对不同变量之间是否存在统计上的显著性关系进行检验，判断P值是否呈现显著性。
2）若呈现显著性，则说明两变量之间存在相关性，反之，则两变量之间不存在相关性。
可以看到显著性P值为0.404，水平上不呈现显著性，不能拒绝原假设，说明两位老师之间不存在一致性。同时，Kappa系数的值为-0.081，因此相关性的程度为极低的一致性。
​

输出结果 2：Kappa 相关系数矩阵热力图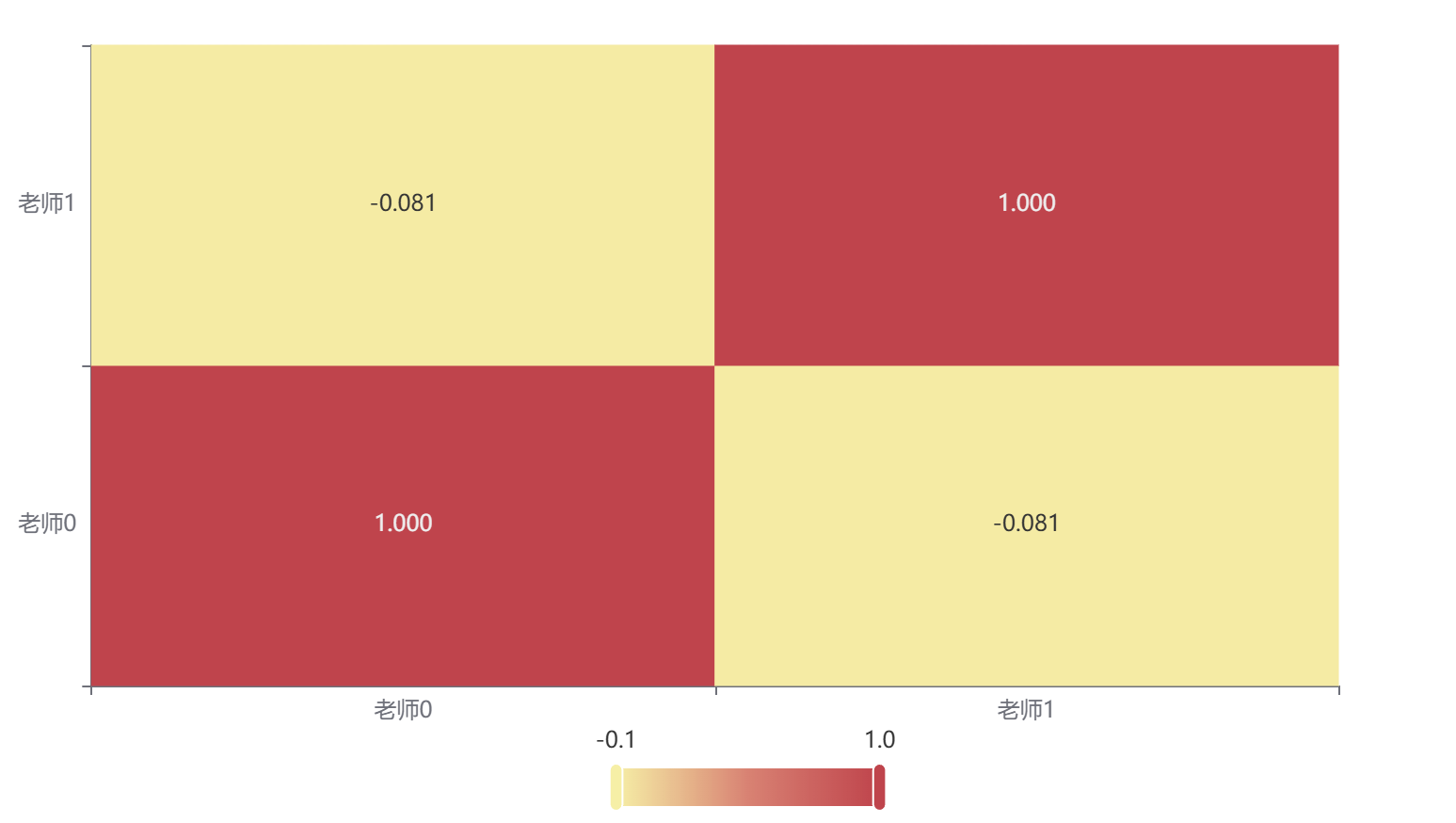

图表说明：
上图展示了热力图的形式展示了 Kappa 值，主要通过颜色深浅去表现值的大小。kappa 值为-0.081，故颜色较淡。

# 7、注意事项

• KAPPA 与其他分析的区别为：

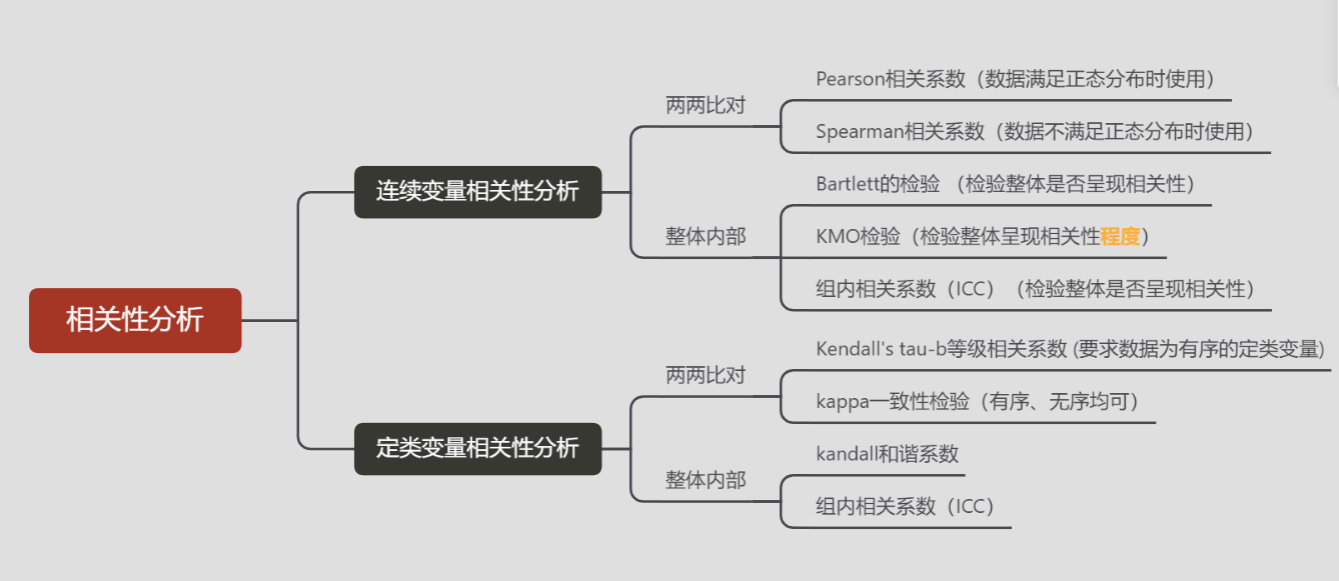
• Kappa 值的大小代表的相关性解释：

# 8、模型理论

kappa 系数是一种衡量分类精度的指标。它是通过把所有地表真实分类中的像元总数（N）乘以混淆矩阵对角线（Xkk）的和，再减去某一类地表真实像元总数与该类中被分类像元总数之积对所有类别求和的结果，再除以总像元数的平方减去某一类地表真实像元总数与该类中被分类像元总数之积对所有类别求和的结果所得到的。

其中，P0是每一类正确分类的样本数量之和除以总样本数，也就是总体分类精度 。
假设每一类的真实样本个数分别为a1,a2,...,aC，而预测出来的每一类的样本个数分别为b1,b2,...,bC
总样本个数为n，则有：

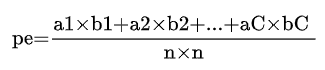
# 9、手推步骤

# Step 1：构建混淆矩阵

两位老师的评分类别为：从不、偶尔、经常。统计实际频数如下：

说明：

• "从不-从不"：学生18、50（共2例）。
• "经常-经常"：学生15、37、48（共3例）。

# Step 2：计算观察一致性比例（$p_o$）

一致情况频数总和：$2+17+3=22$
总样本数：$n=50$

$p_o=\frac{22}{50}=0.44$

# Step 3：计算期望一致性比例（$p_e$）

计算每个类别的边际比例乘积之和：

$p_e=\frac{(8\times 12)+(29\times 33)+(17\times 9)}{50\times 50}=\frac{96+957+153}{2500}=\frac{1206}{2500}=0.4824$

# Step 4：计算Kappa系数（$k$）

代入公式：

$k=\frac{p_o-p_e}{1-p_e}=\frac{0.44-0.4824}{1-0.4824}=\frac{-0.0424}{0.5176}\approx -0.081$

# Step 5:计算标准误差（$SE$）与 $Z$ 值

标准误差公式：

$SE=\sqrt{\frac{p_o(1-p_o)}{n(1-p_e{)}^2}}=\sqrt{\frac{0.44\times 0.56}{50\times (1-0.4824{)}^2}}\approx 0.097$

$Z$ 值：

$Z=\frac{k}{SE}=\frac{-0.081}{0.097}\approx -0.835$

显著性检验:根据$Z$值查标准正态分布表，得P值约为0.404（双尾检验）。由于$P>0.05$，无显著一致性,，无法拒绝原假设。

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]唐万, 胡俊, 张晖,等. Kappa 系数:一种衡量评估者间一致性的常用方法(英文)[J]. 上海精神医学(Shanghai Archives of Psychiatry), 2015(1):62-67.