Cochran's Q检验

操作视频

# 1、作用

Cochran's Q 检验也是用于非参数差异性检验的一种，适用于分析多个样本（样本数一致）差异性的统计检验，用于三个字段以上的数据的总体差异性的统计检验。与 Friedman 检验与 Nemenyi 检验不一样的是，Cochran's Q 检验只适用定类字段。

# 2、输入输出描述

输入：三个或以上的二分类定类变量变量。
输出：变量整体上是否呈现显著性差异。

# 3、案例示例

分析 50 个同学对一模、二模、三模的三次高考模拟考试的体验，体验分为难或简单，检验三次考试难度是否一样。

# 4、案例数据

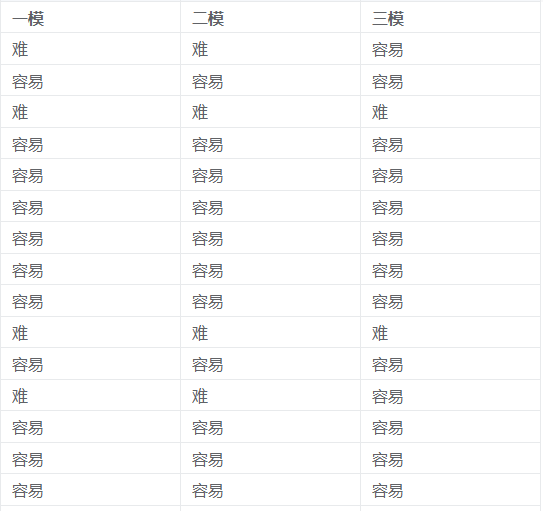
Cochran's Q 检验案例数据

# 5、案例操作

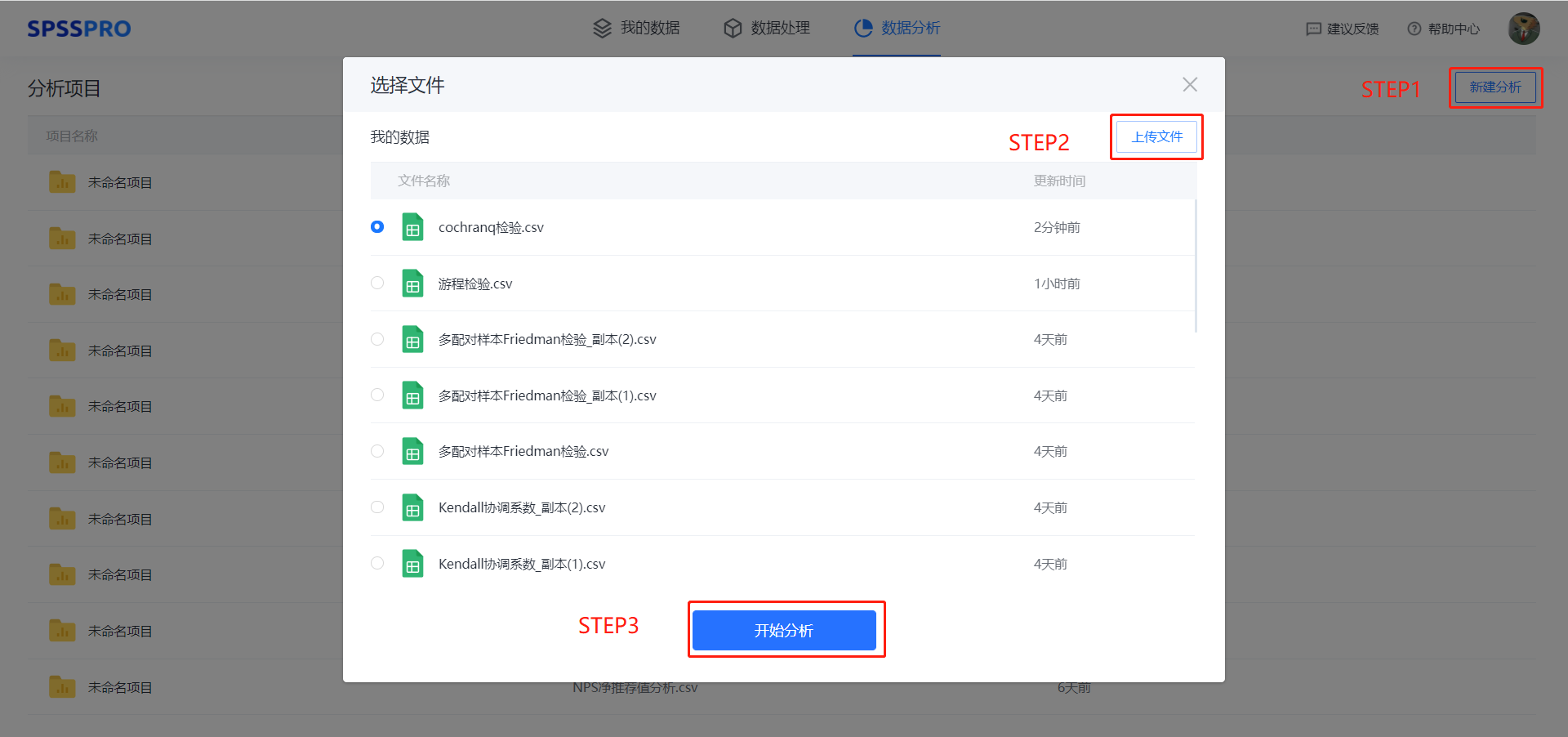
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；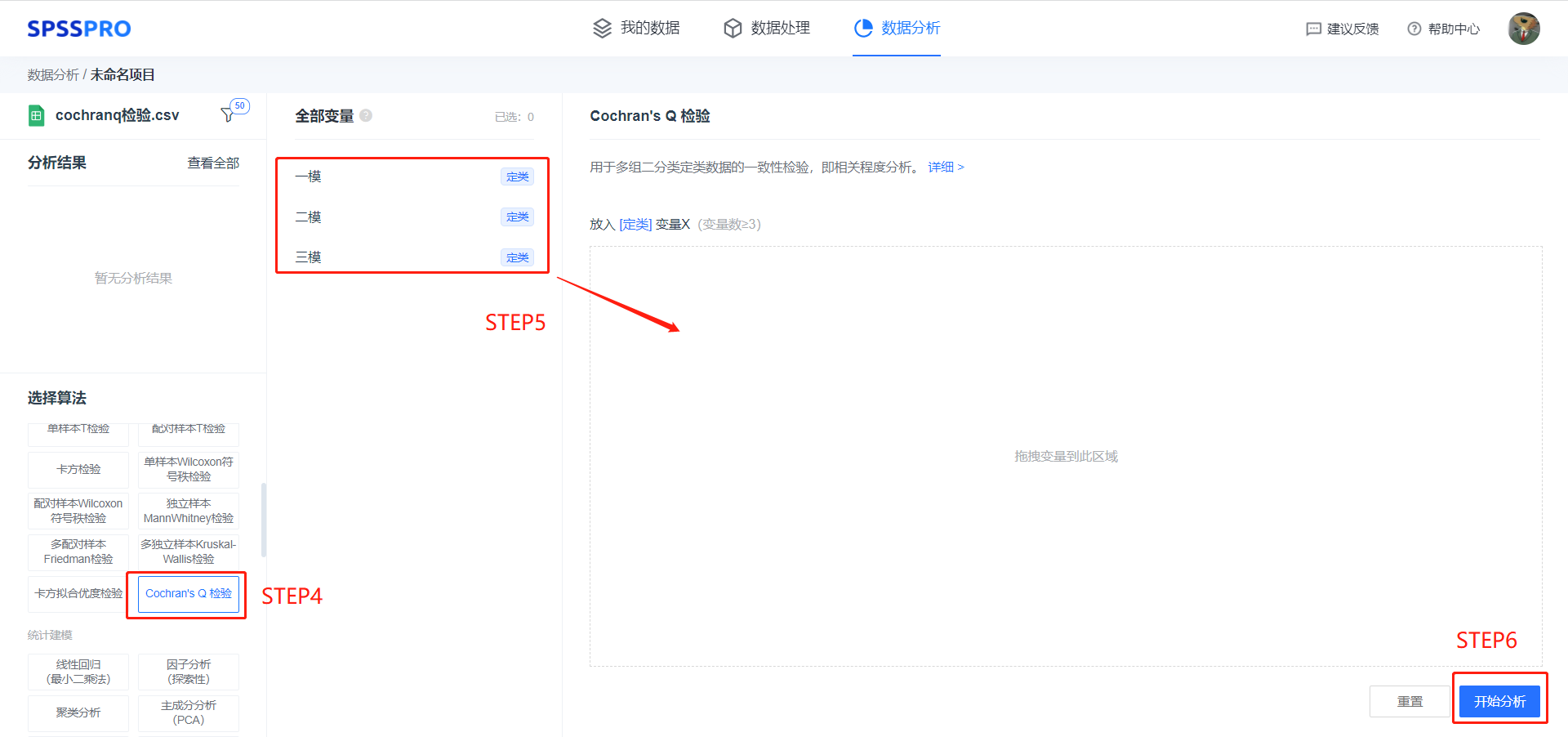

step4：选择【Cochran's Q 检验】；
step5：查看对应的数据数据格式，【Cochran's Q 检验】要求输入数据为分组定类变量 X，（变量数>=3）；
step6：点击【开始分析】，完成全部操作；

# 6、输出结果分析

输出结果 1：Cochran's Q 检验

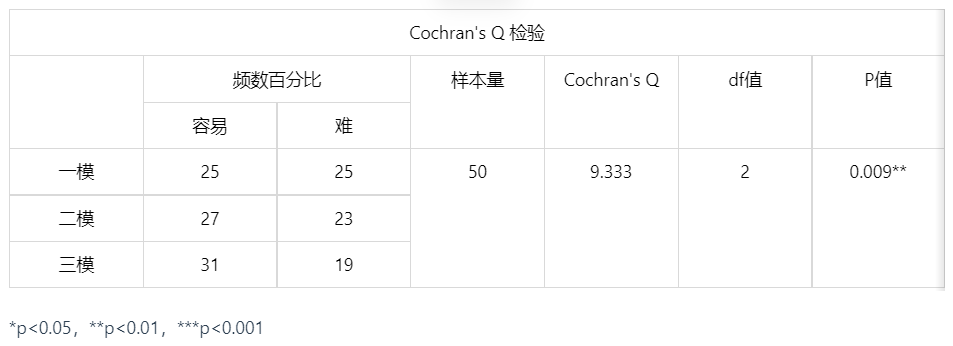
图表说明：Cochran’s Q 检验的结果显示，基于字段:一模、二模、三模：整体的显著性 P 值为 0.009，水平上呈现显著性，拒绝原假设，因此说明数据总体存在差异性，可以认为三次考试难度不一样。

输出结果 2：频数分析堆叠图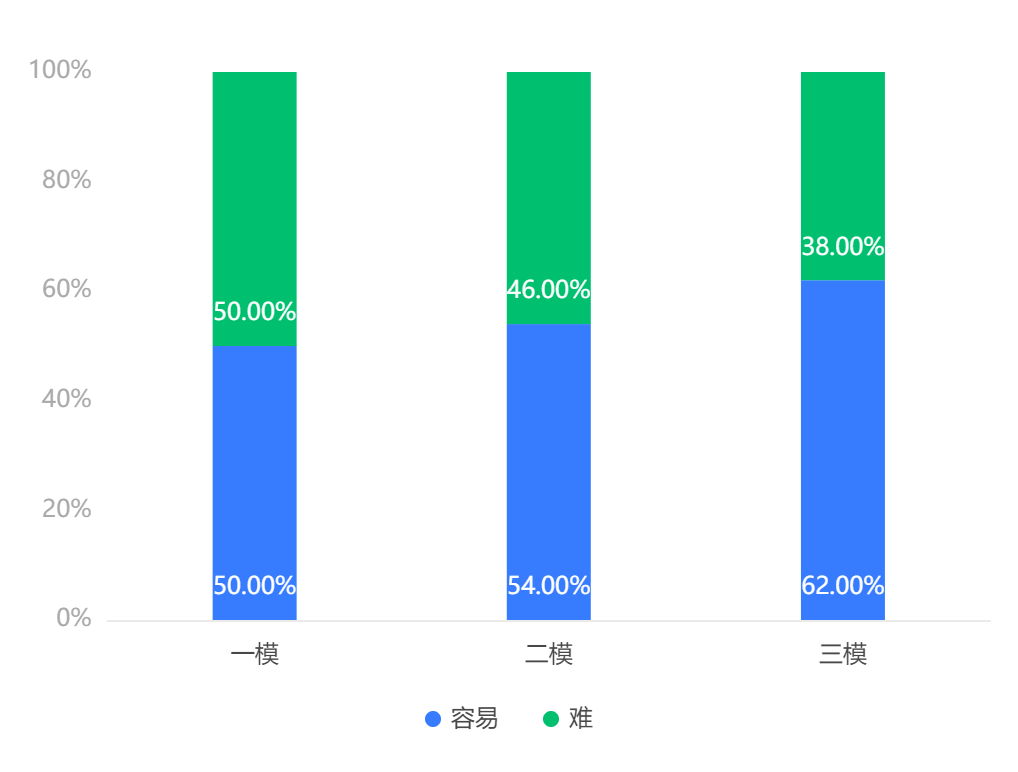

图表说明：上图以堆叠直方图展示了二分类变量的情况。可见考试难度一次比一次简单。

# 7、注意事项

必须为 2 分类变量，如果不是 0、1 格式的二分类变量，SPSSPRO 会自动在后台转换为 0、1 格式再运行 Cochran's Q 检验。

# 8、模型理论

若有 k 个相关样本,每个样本有 n 个观测结果，检验 k 个样本间是否有显著差异，可以建立双侧备择，假设组为：
H0:k 个样本间无显著差异
H1:k 个样本间有显著差异
由于三个以及三个以上样本间的差异的方向不便于判定，因而，通常只建立双侧备择进行检验。
为对假设作出判定，所分析的数据测量层次为定类尺度即可。获得的数据可排成一个 n 行 k 列的表。如果 H0 为真，那么将测量结果分为"成功"和"失败"的话，"成功"和"失败"应随机地分布在表中的各行各列。
Cochran's Q 统计量的定义为：

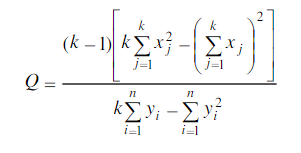
式中，xj是第j列的总数，yi是第i行的总数。

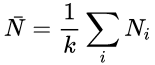
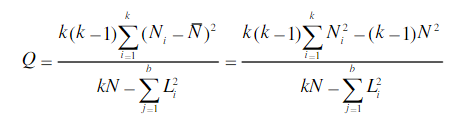
式中，k为处理数；b为区组数;N为行总和;L为列总和；
由于Q统计量的抽样分布近似为自由度df = k - 1的

分布，所以根据自由度df = k - 1,给定的显著性水平α，能够在附表中查找

α，若Q >=

α则在显著性水平α下拒绝 $H_0$ ，表明样本之间存在着显著差异。

# 9、手推步骤

# Step 1: 数据准备

将数据中的“难”更改为 $0$ ，“容易”更改为 $1$ 。三个模型（一模、二模、三模）的频数统计如下：

一模：难=25，容易=25
二模：难=23，容易=27
三模：难=19，容易=31
样本量 $n = 50$ ，处理数 $k = 3$ 。

# Step 2: 列总和计算

计算如下：

$x_{1} = 25, x_{2} = 27, x_{3} = 31$

$\sum x_{j} = 25 + 27 + 31 = 83$

$\sum x_{j}^{2} = 25^{2} + 27^{2} + 31^{2} = 625 + 729 + 961 = 2315$

# Step 3: 行总和计算

$y_{i} = 0$ 的样本数：17
$y_{i} = 1$ 的样本数：4
$y_{i} = 2$ 的样本数：2
$y_{i} = 3$ 的样本数：27
$\sum y_{i} = (0 \times 17) + (1 \times 4) + (2 \times 2) + (3 \times 27) = 89$

$\sum y_{i}^{2} = (0^{2} \times 17) + (1^{2} \times 4) + (2^{2} \times 2) + (3^{2} \times 27) = 255$

# Step 4: $Q$ 值计算

计算过程如下：

$分子 = (3 - 1) [3 \times 2315 - 83^{2}] = 2 \times (6945 - 6889) = 112$

$分母 = 3 \times 89 - 255 = 12$

$Q = \frac{112}{12} \approx 9.333$

# Step 5: 显著性检验

自由度 $d f = k - 1 = 2$
查卡方分布表， $Q = 9.333$ 对应的 $P 值 \approx 0.009$ （显著性水平 $α = 0.01$ ）

# 10、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]茆诗松, 王静龙, 濮晓龙, 等. 高等数理统计 (第二版)[M]. 北京: 高等教育出版社, 2006.
[3]王重, 刘黎明. 拟合优度检验统计量的设定方法[J]. 统计与决策, 2010(5):154-156.

建议反馈