正态性分析

操作视频

SPSSPRO教程-正态性分析

# 正态性分析

# 1、作用

正态性分析是统计学中用来检验数据是否符合正态分布的方法和技术。正态分布（也称为高斯分布）是一种对称的概率分布，其特点是均值、中位数和众数相等，而且数据围绕均值对称分布，形成一个钟形曲线。

许多经典的推断统计方法，如 t 检验、ANOVA（方差分析）、线性回归等，都基于数据服从正态分布的假设。当数据近似正态分布时，这些方法通常具有更好的效果和可靠性。

# 2、输入输出描述

输入：一个或多个定量变量（如 30 名员工这个月的工资）。
输出：模型检验的结果，数据满足/不满足正态分布。

# 3、案例示例

案例：电信公司需要检验用户电话银行月费和最近一个月消费金额是否满足正态性。
PS：

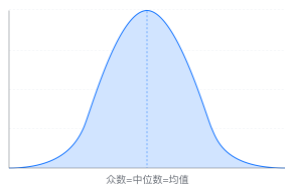
正态性分析案例示例

标准正态分布特征：均值=中位数=众数；
右偏态特征：众数<中位数<均值；
左偏态特征：众数>中位数>均值。

# 4、案例数据

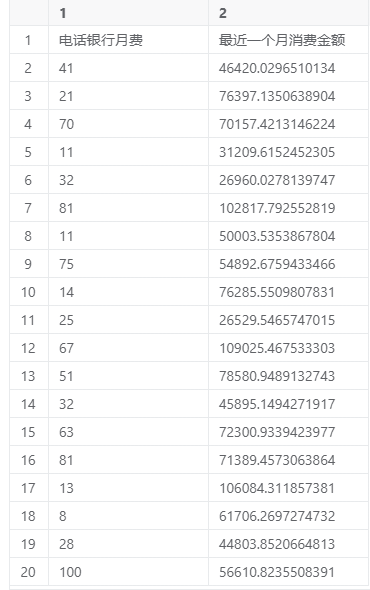
正态性分析案例数据

一个或多个定量变量指的是：一个或多个定量变量(电话银行月费/最近一个月消费金额)为变量X。
若输入多个定量变量，则对多个定量变量重复进行正态性分析。

# 5、案例操作

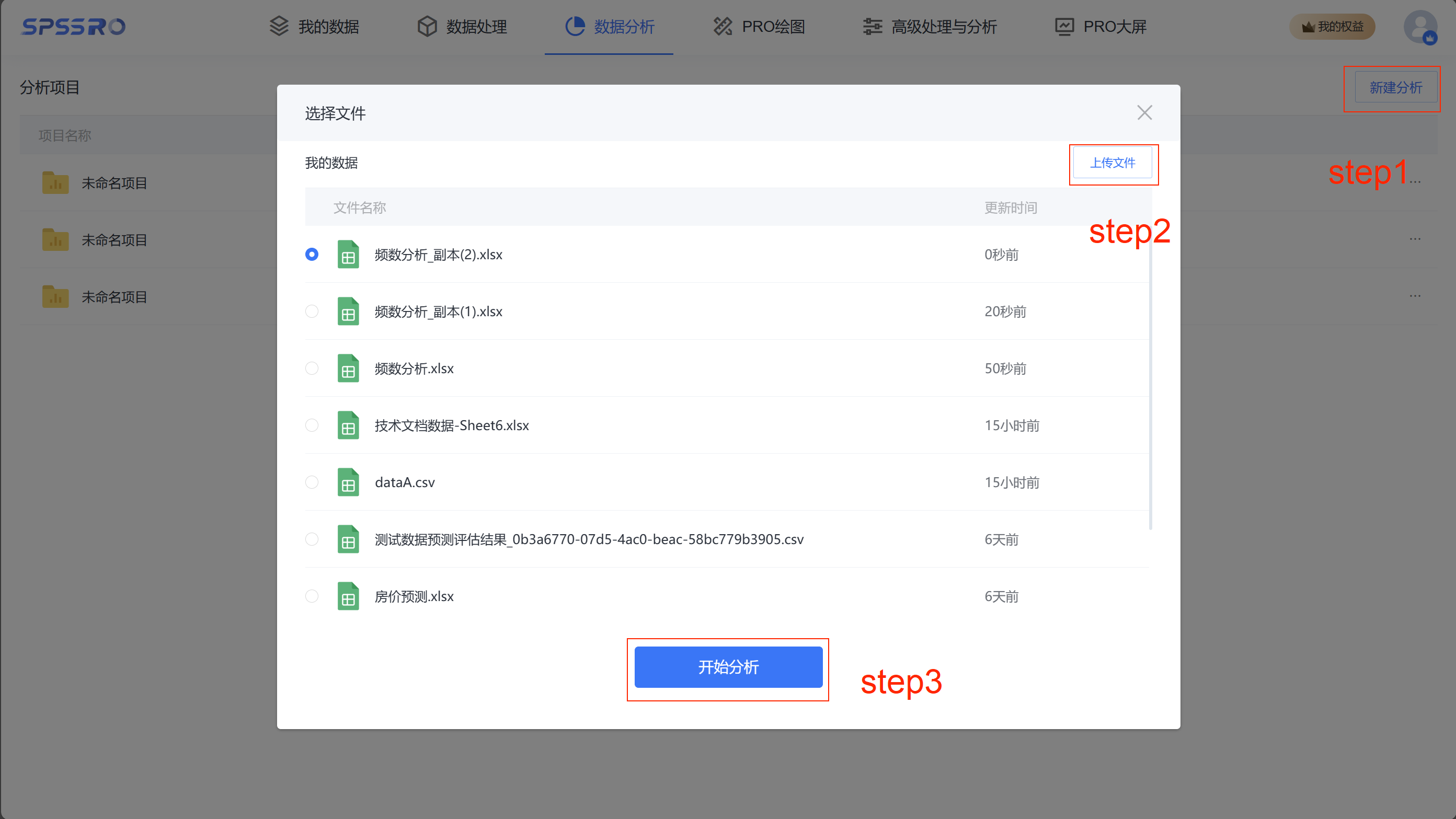Step1：新建分析；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

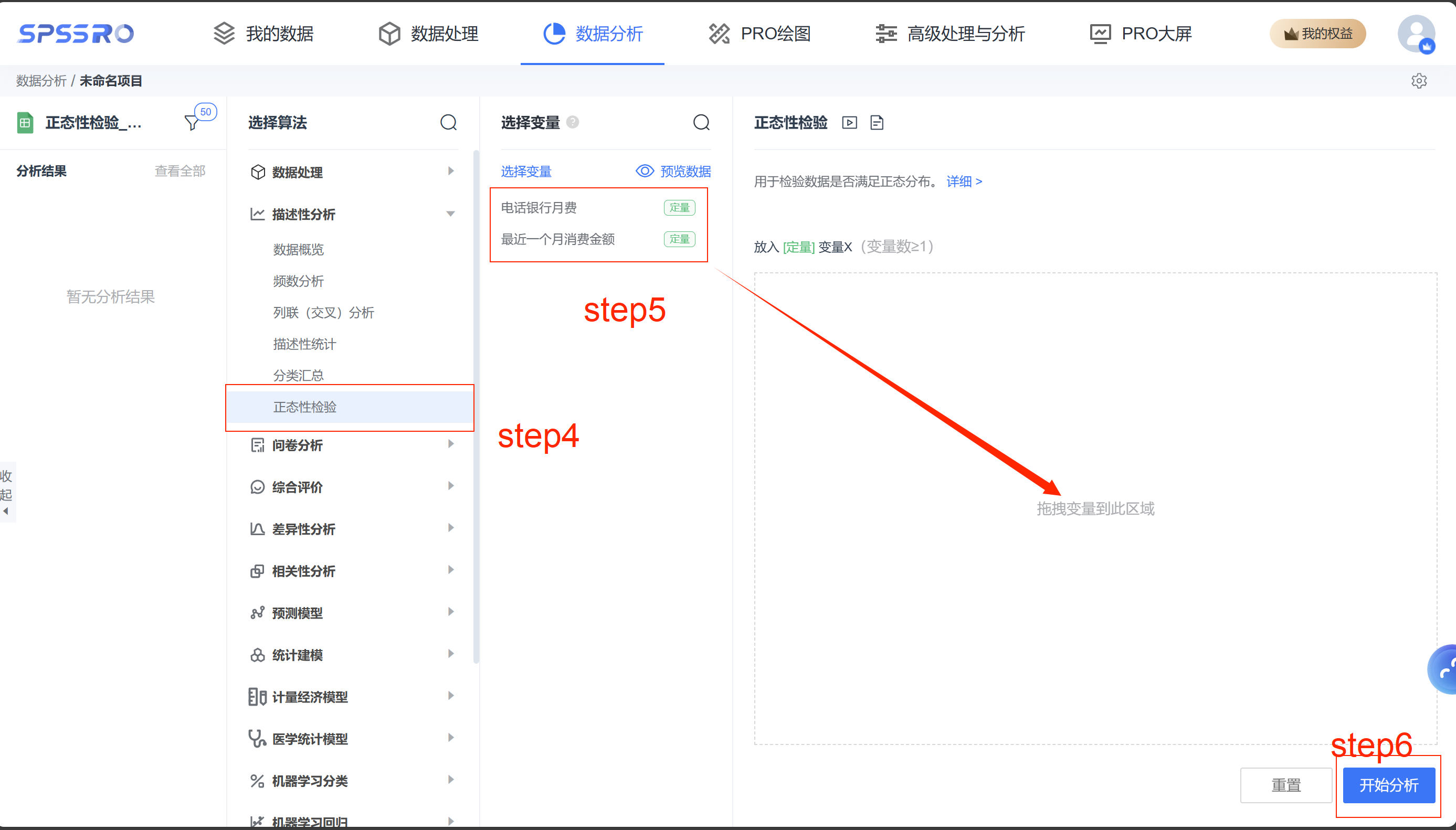
Step4：选择【正态性检验】；
Step5：查看对应的数据数据格式，【正态性检验】要求输入数据为定量变量，且至少有一项；
Step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：总体描述结果

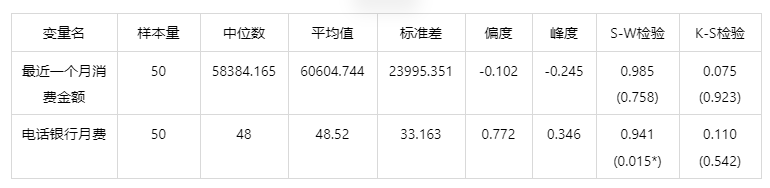
图表说明:上表展示了电话银行月费、最近一个月消费金额描述性统计和正态性检验的结果，包括中位数、平均值等，用于检验数据的正态性。以电话银行月费样本为例，电话银行月费样本【N <= 5000，采用 S-W 检验】，显著性 P 值为 0.015，水平呈现显著性，拒绝原假设，因此数据不满足正态分布。
结果分析：根据检验来看，最近一个月消费金额满足正态性，电话银行月费不满足正态性，然而通常现实研究情况下很难满足检验，若其样本峰度绝对值小于10并且偏度绝对值小于3，结合正态分布直方图、PP图或者QQ图可以描述为基本符合正态分布。

输出结果 2：正态性检验直方图

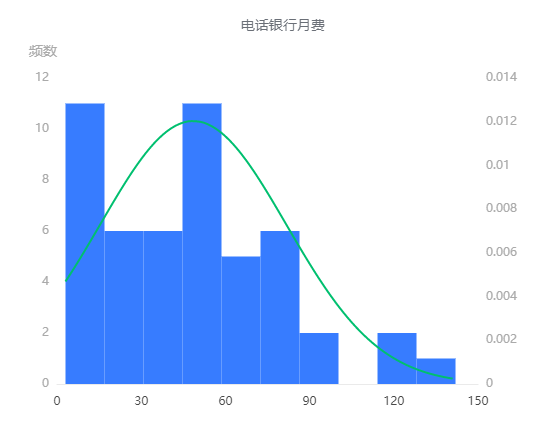
正态性检验直方图

图表说明：上图展示了电话银行月费数据正态性检验的结果，若正态图基本上呈现出钟形（中间高，两端低），则说明数据虽然不是绝对正态，但基本可接受为正态分布。
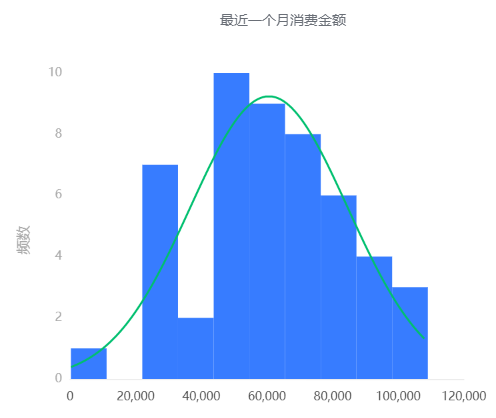
结果分析：根据正态性检验直方图来看，电话银行月费的正态性检验直方图没有呈现出钟形，可以认为其不是正态数据；最近一个月消费金额的正态性检验直方图较为明显为钟形，故满足正态性。

输出结果 3：正态性检验 P-P 图

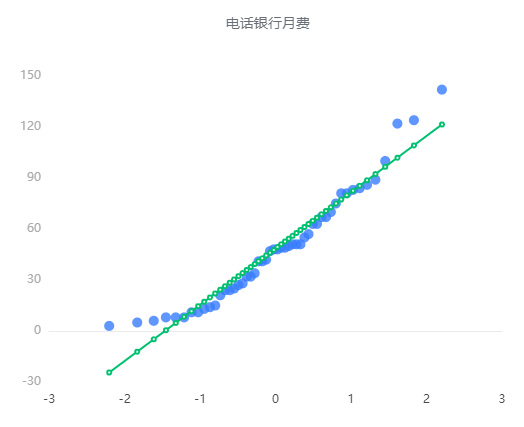
正态性检验 P-P 图

图表说明：上图是电话银行月费计算观测的累计概率（P）与正态累计概率（P）的拟合情况。拟合程度越高越服从正态分布。
结果分析：根据P-P图结果，电话银行月费的拟合情况在最大值最小值附近较为不佳。

输出结果 4：正态性检验 Q-Q 图

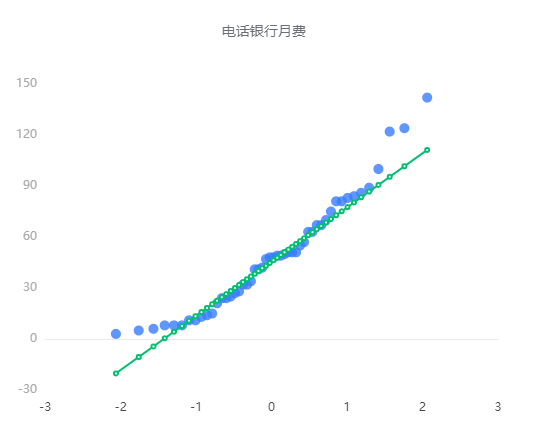
正态性检验 Q-Q 图

图表说明：Q-Q 图，全称“Quantile Quantile Plot”用图形的方式比较观测值与预测值（假定正态下的分布）不同分位数的概率分布，从而检验是否吻合正态分布规律。并且将实际数据作为 X 轴，将假定正态时的数据分位数作为 Y 轴，作散点图，散点与直线重合度越高越服从正态分布，散点差异愈大越不服从正态分布，请视实际情况而定。
结果分析：根据Q-Q图结果，电话银行月费的拟合情况在最大值最小值附近较为不佳。

# 7、注意事项

通常现实研究情况下很难满足检验，若其样本峰度绝对值小于 10 并且偏度绝对值小于 3，结合正态分布直方图、PP 图或者 QQ 图可以描述为基本符合正态分布；
若正态分布直方图基本上呈现出钟形（中间高，两端低），则说明数据虽然不是绝对正态，但基本可接受为正态分布；
小数据样本即一般样本数 50 以下进行 Shapiro-Wilk，大数据样本即一般样本数 50 以上使用 Kolmogorov–Smirnov 检验。

# 8、模型理论

# 正态分布（Normal distribution)

也称“常态分布”，又名高斯分布（Gaussian distribution），最早由棣莫弗（Abraham de Moivre）在求二项分布的渐近公式中得到。高斯在研究测量误差时从另一个角度导出了它。拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。若随机变量 $X$ 服从一个位置参数为 $μ$ 、尺度参数为 $σ$ 的正态分布，记为：

X \sim N (μ, σ^{2})

其中， $μ$ 是分布的均值（位置参数），决定了分布的中心位置； $σ^{2}$ 是方差（尺度参数），决定了分布的离散程度；

我们通常所说的标准正态分布是位置参数 $μ = 0$ ，尺度参数 $σ^{2} = 1$ 的正态分布（见下图中红色曲线）。

钟形曲线

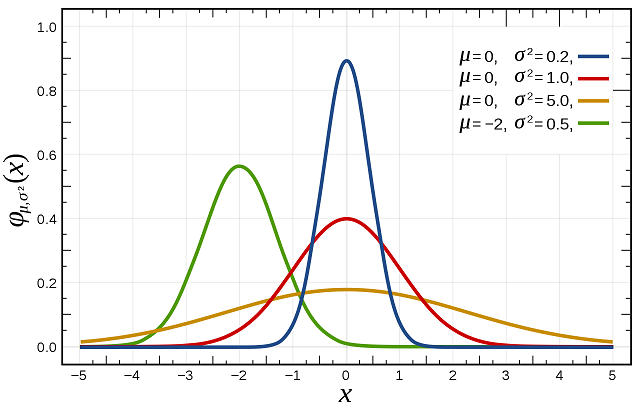
在数学上，正态分布（或高斯分布）是一种连续型概率分布，它的概率密度函数（Probability Density Function, PDF）可以用来描述随机变量的分布情况:

f (x) = \frac{1}{σ \sqrt{2 π}} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}}

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线。

正态分布的性质有：

对称性： 正态分布是对称的，以均值 $μ$ 为中心，左右对称。
集中度： 由均值 $μ$ 控制，均值越高，分布越向右移动；均值越低，分布越向左移动。
离散程度： 由标准差 $σ$ 控制，标准差越大，数据越分散；标准差越小，数据越集中。

# QQ图

QQ 图（Quantile-Quantile Plot）是一种用于比较两个数据集是否来自同一分布的图形工具。它通过将一个数据集的分位数与另一个数据集的理论分位数进行比较来帮助我们评估数据的正态性或其他分布假设。

在 QQ 图中，通常将一个数据集的分位数（实际观测值）对应于另一个数据集的分位数（理论分位数）。如果两个数据集来自相同的分布，那么 QQ 图上的点将大致落在一条对角线上。如果数据不符合正态分布，点将偏离对角线。

其计算步骤为：

数据排序： 首先，将观测数据集 $X$ 和理论数据集 $Y$ 分别进行排序。
计算分位数： 对于每个数据集，计算对应的分位数。对于观测数据集 $X$ ，第 $i$ 个观测值 $x_{(i)}$ 的分位数可以表示为 $F_{X} (x_{(i)})$ ，其中， $F_{X}$ 是观测数据集 $X$ 的累积分布函数（CDF）。设 $X$ 的概率密度函数（Probability Density Function，PDF）或概率质量函数（Probability Mass Function，PMF）为 $f (x)$ ，则 $X$ 的CDF可以定义为：

F (x) = P (X \leq x) = \int_{- \infty}^{x} f (t) d t

同理，计算理论数据集 $Y$ 的CDF。

绘制： 在 QQ 图中，将 $X$ 的分位数 $F_{X} (x_{(i)})$ 绘制在横轴上，将 $Y$ 的分位数 $F_{Y} (y_{(i)})$ 绘制在纵轴上。理论上，如果 $X$ 和 $Y$ 来自于相同的分布，则这些点应当大致落在一条直线上。

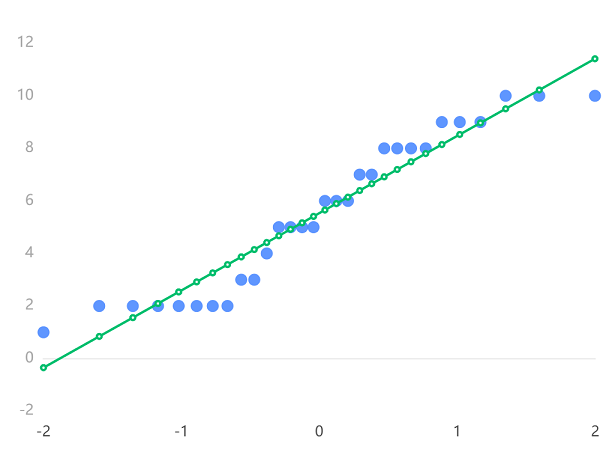
Q-Q 图

# P-P 图

PP图（Probability Plot，概率图）是一种用于检验数据是否符合特定分布的图形方法。它通过比较观测数据的累积分布函数（CDF）与理论分布的累积分布函数，来评估数据的拟合程度。P-P 图可以有效地检验数据是否遵循指定的理论分布。当数据完全符合指定分布时，P-P 图中的点近似于一条直线。

如果在P-P 图中，点的分布形状不是直线，但显示出一定的规律性，可以考虑对变量数据进行适当的转换，以使转换后的数据更接近指定的理论分布。

其绘制方法与QQ图基本类似：

计算累积分布函数： 对于每个数据点，计算其在整个数据集中的排位百分比（即累积分布函数值），用来代表数据的累积分布情况。
理论分布的累积分布函数： 根据假设的理论分布（比如正态分布），计算出每个数据点对应的理论累积分布函数值。
绘制PP图： 将实际观测的累积分布函数值（横坐标）与理论分布的累积分布函数值（纵坐标）进行比较，并用散点图或线图展示。如果数据服从假设的理论分布，则散点图或线图会接近一条对角线。

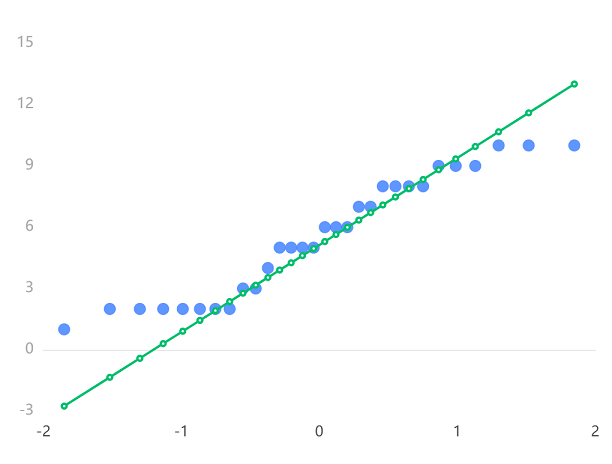
P-P 图

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Shaou-Gang Miaou; Jin-Syan Chou. 《Fundamentals of probability and statistics》. 高立图书. 2012: 第 147 页. ISBN 9789864128990.
[3] Casella & Berger (2001, p. 102)
[4] 宗序平, 姚玉兰. 利用 Q-Q 图与 P-P 图快速检验数据的统计分布[J]. 统计与决策, 2010, 000(020):151-152.

建议反馈