描述性统计

操作视频

SPSSPRO教程-描述性统计

# 描述性统计

# 1、作用

描述性统计是统计学中的一项基础方法，用于对数据进行概括、总结和描述。它主要通过一些统计指标和图表来分析数据的集中趋势、分散程度和分布形状，而不涉及对数据背后的原因或推断进行分析。

描述性统计广泛应用于各个学科和行业，包括社会科学、自然科学、经济学、医学等。比如，在市场调研中，用于总结消费者偏好和市场趋势；在财务分析中，用于分析公司的财务表现和风险管理；在医学研究中，用于描述患者群体的基本特征和病情分布。

# 2、输入输出描述

输入：一个或多个定量变量。
输出：对总体数据的各项统计指标（字段）进行整体描述分析，包括样本量、最大值、最小值、算术平均值、中位数等统计量。

# 3、案例示例

案例：对某个学校某次期末考试成绩进行描述统计分析可以查看这次考试的平均成绩、最高分、最低分，成绩集中在哪个分数段等。

# 4、案例数据

描述性统计案例数据

一个或多个定量变量指的是：一个或多个定量变量(语文/数学/英语等定量变量)，若输入多个/定量变量，对多个定量变量重复分析。

# 5、案例操作

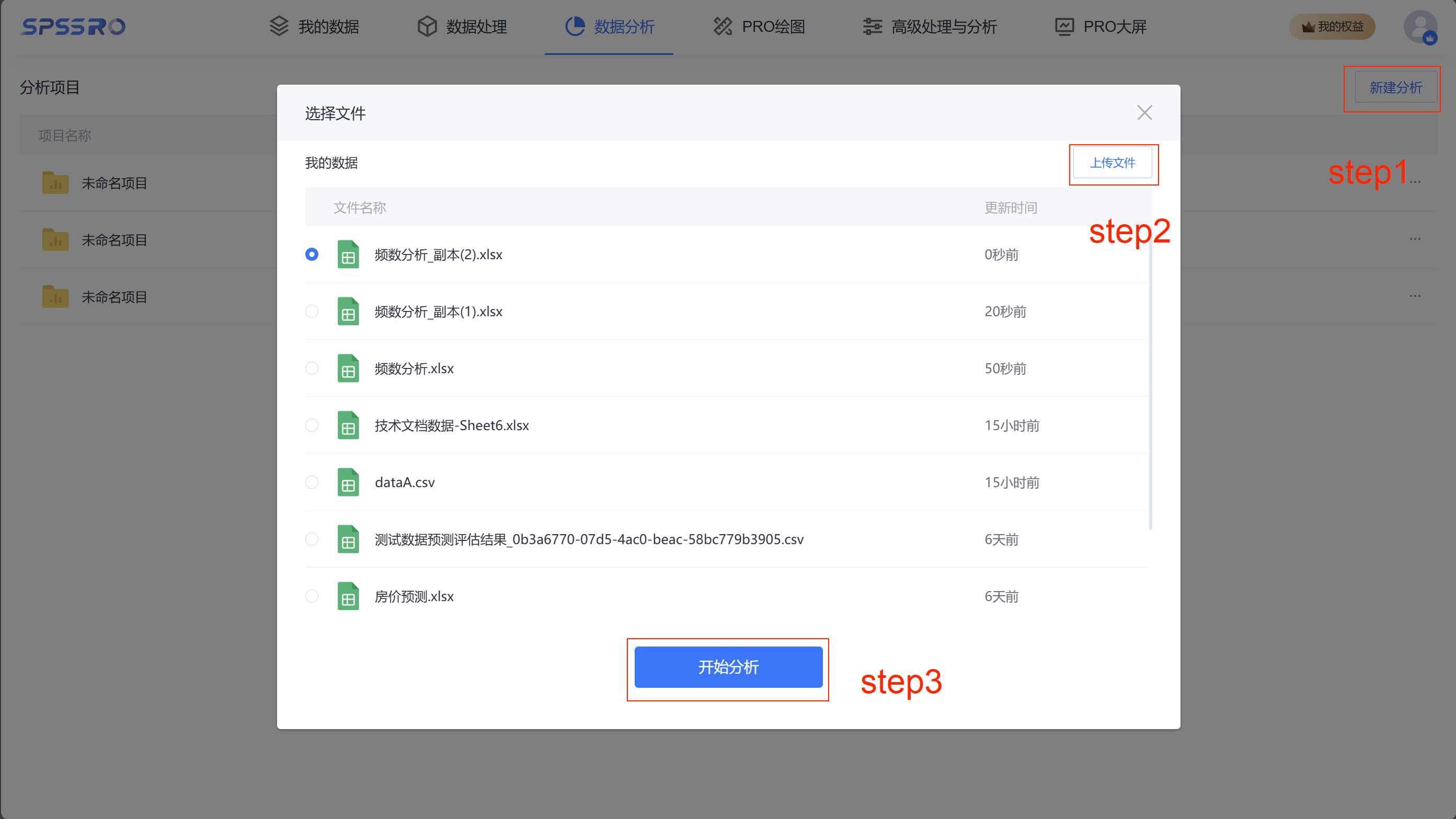Step1：新建分析；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；
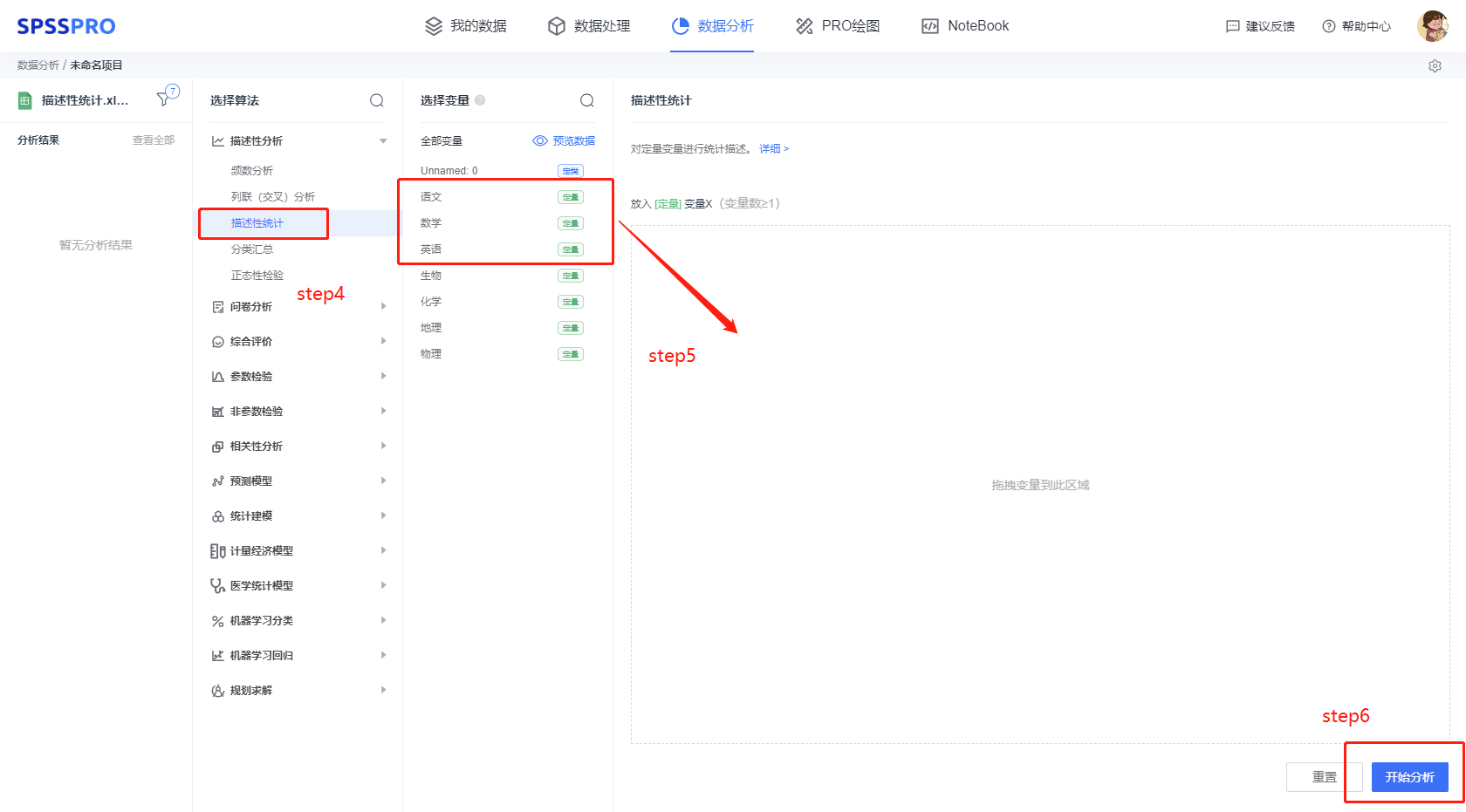描述性统计案例操作 Step4：选择【描述性分析】；
Step5：查看对应的数据数据格式，【描述性分析】要求输入数据为定量变量，且至少有一项，本例拖入三个定量变量【语文】、【数学】、【英语】，这里针对这三项定量变量的输出结果进行分析。；
Step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：总体描述结果 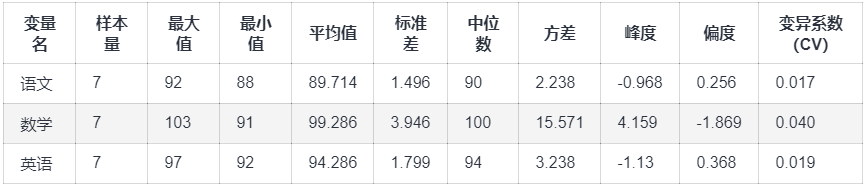图表说明：上表展示了描述性统计的结果，包括样本量、最大值、最小值等统计量，用于研究定量数据的整体情况。
1.分析各项统计指标，对各项统计指标进行整体描述分析。
2.对异常的或者表现得较为突出的指标进行分析，例如高方差，高平均值等等。
结果分析：分析结果该校学生数学成绩的平均值最高，语文成绩的平均值最低。

输出结果 2：散点图 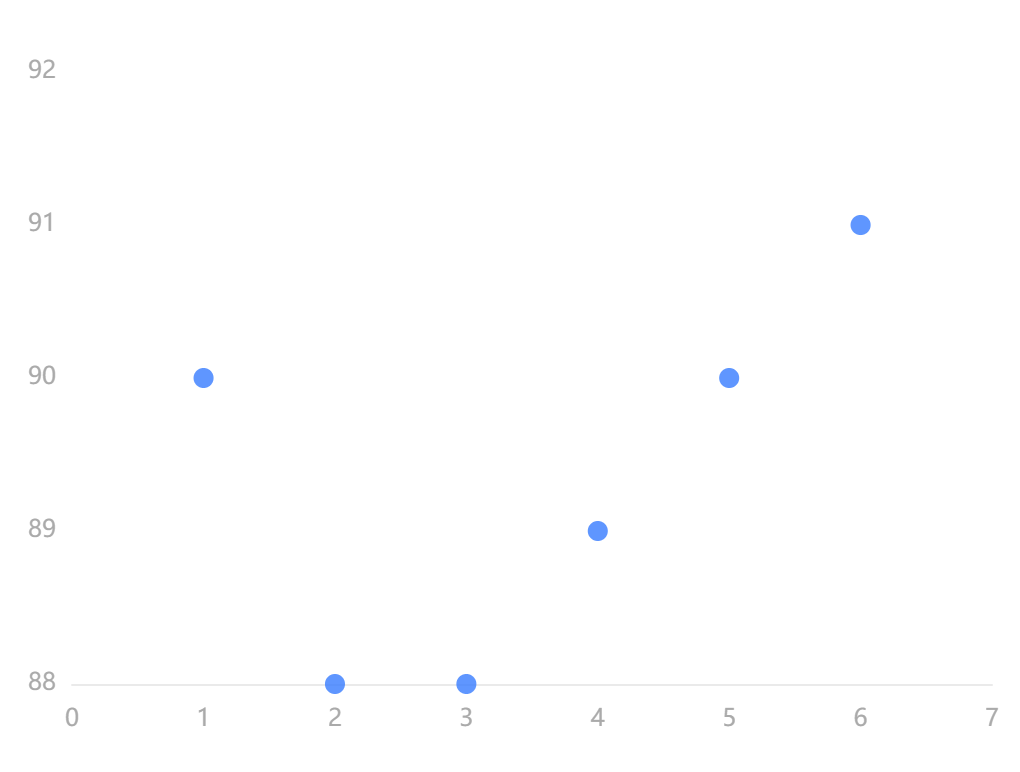描述性统计散点图 图表说明：上图以散点图的形式展示了集中趋势分析的结果，可以用来估计或预测总体。

输出结果 3：箱型图 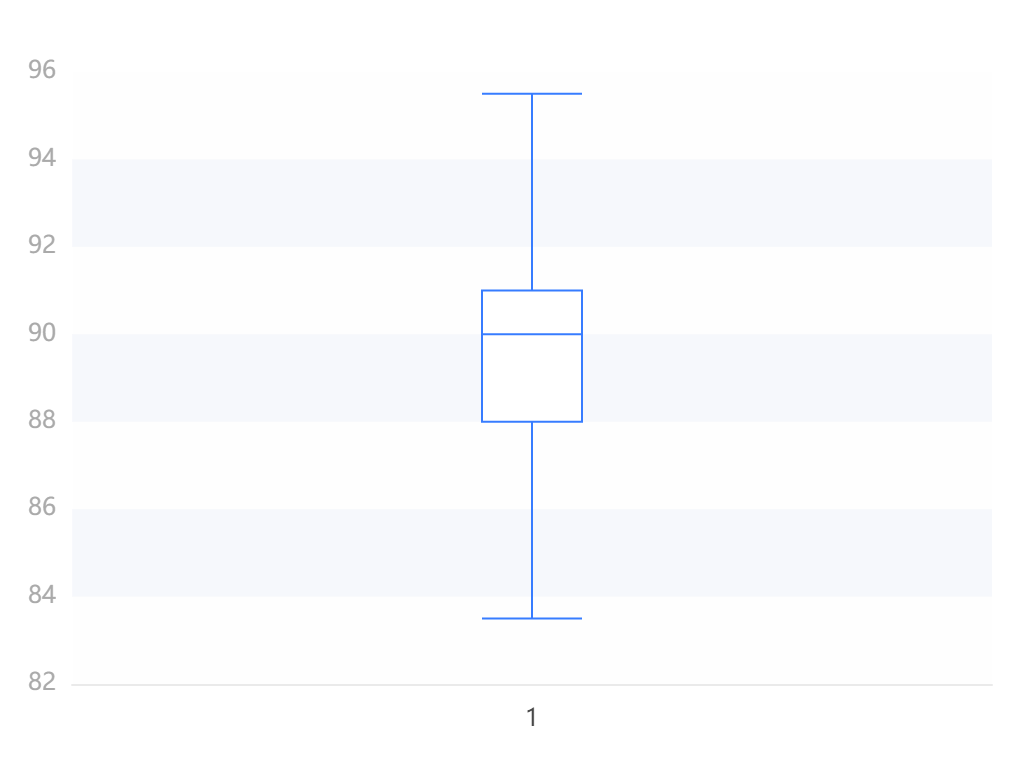描述性统计箱型图 图表说明：上图以箱线图的形式展示了离散趋势分析的结果，离散趋势用极大值、极小值、25%分位数、中位数、75%分位数等统计指标对数据分布进行差异（稳定性）测量。
PS:极大值、极小值并非该数据的最大值、最小值，该值为箱线图的内限，即大于极大值或小于极小值的点视为异常点。
结果分析：该箱型图展示了语文成绩的数据分散结果。

# 7、注意事项

一般来说，描述性统计是包含针对定类数据的频数统计与针对定量数据的集中趋势分析、离散程度分析，SPSSPRO 的将针对定类数据的拆为频数分析，描述性统计专门对于定量数据进行统计描述。

# 8、模型理论

描述性统计分析涉及对调查总体中所有变量的数据进行统计性描述，主要包括数据的频数分析（在 SPSSPRO 中称为频数分析）、数据的集中趋势分析、数据的离散程度分析、数据的分布以及一些基本的统计图形展示。

常用的统计指标包括平均值、中位数、四分位数、方差、标准差、变异系数等。

# 集中趋势

集中趋势是描述数据分布中心位置的统计指标，用于了解数据的平均水平或中心位置。常见的集中趋势指标包括平均值（均值）、中位数和众数。

众数（Mode）： 是一组数据中出现频率最高的数值。作为一种位置平均数，众数不受极端值的影响，在实际工作中应用广泛。当数据集合数量较大且具有明显的集中趋势时，可以用众数来代表集中趋势的值。
平均数（Mean）： 指的是算术平均数，也称为均值。在统计学中，均值是集中趋势的主要测度值，具有重要的应用价值。
中位数（Median）： 是将一组数据按照大小顺序排列后位于中间位置的数值。作为一种位置平均数，中位数不受极端值的影响。特别适用于数据变量差异较大或频数分布为偏态的情况，比算术平均数更具有代表性。在缺少精确测量手段时，中位数也可以近似代替算术平均数。
平均差（Mean Deviation）： 指的是各个数据值与平均数的离差绝对值的算术平均数。平均差异越大，表示各数据值与平均数的差异程度越大，平均数的代表性就越小；反之，平均差越小，则表示各数据值与平均数的差异越小，平均数的代表性就越大。

# 离散程度

离散程度是描述数据分布的离散程度或者波动性的统计指标。

最大值： 一组数中的最大值。
最小值： 一组数中的最小值。
极差： 一组数中最大值与最小值之差。 $R a n g e = m a x (X) - m i n (X)$
方差： 方差是各个数据点与其算术平均数的离差平方的算术平均数。方差的计算单位和量纲不便于从经济意义上进行解释，因此实际统计工作中常用方差的算术平方根——标准差来衡量总体的离散程度。

Var (X) = \frac{1}{n} \sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}

标准差： 标准差又称均方差，具有量纲，与变量值的计量单位一致。

SD (X) = \sqrt{Var (X)}

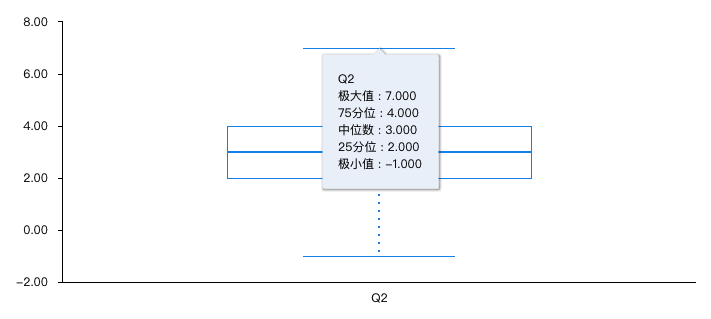
25分位（Q1）： 第一四分位数(Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字。
75分位（Q2）： 第三四分位数(Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。
四分位差(IQR)： 四分位差（quartile deviation），它是上四分位数（Q3，即位于75%）与下四分位数（Q1，即位于25%）的差。四分位差反映了中间50%数据的离散程度，其数值越小，说明中间的数据越集中；其数值越大，说明中间的数据越分散。四分位差不受极值的影响。

I Q R = Q 3 - Q 1

异众比率（Coefficient of Variation）： 总体中非众数次数与总体全部次数之比。异众比率衡量非众数的频数在总频数中的比例。虽然也是反映离散程度的相对指标，但与标准差系数不同。异众比率主要用于评估众数对数据集的代表性。异众比率越大，表示说明非众数组的频数占总频数的比重越大，众数的代表性较差；异众比率越小，表示非众数组的频数占总频数的比重越小,众数的代表性较好。
标准误（Standard Error of Mean，SEM）： 标准误描述了均值抽样分布的离散程度和均值抽样误差的尺度。标准误是样本均值的标准差，反映了样本均值之间的变异。标准误用于衡量抽样误差和推断总体参数的可靠性。标准误越小，表明样本统计量与总体参数的值越接近，样本对总体越有代表性，用样本统计量推断总体参数的可靠度越大。因此，标准误是统计推断可靠性的指标。

SEM = \frac{SD}{\sqrt{n}}

离散系数（Coefficient of Variation，CV）： 离散系数又称变异系数，是用于比较不同样本数据离散程度的相对统计量。离散系数大表示数据的离散程度大；离散系数小表示数据的离散程度小。

CV = (\frac{SD}{\bar{x}}) \times 100 %

离散程度表

离散程度图

# 分布情况

分布情况是描述数据如何分布在不同数值或区间内的统计特征。在统计学中，常用峰度和偏度来描述数据分布的形状和偏斜程度：

1. 峰度（Kurtosis）： 峰度是描述分布形状尖峭程度的统计量。具体来说，它衡量了分布中数据集中在中心位置附近的相对大小，以及尾部数据相对于中心位置的分布情况。

峰度大于3：尖峰（Leptokurtic），表示数据集中在中心附近的数据比较集中，尾部数据比较少，分布较为尖锐。
峰度等于3：正态分布（Mesokurtic），表示数据的分布符合正态分布的标准。
峰度小于3：扁平（Platykurtic），表示数据集中在中心附近的数据相对较少，分布比较平坦，尾部数据相对较多。

2. 偏度（Skewness）： 偏度是描述分布偏斜方向和程度的统计量。如果数据分布是对称的，则偏度为0；如果数据分布向右偏（正偏），偏度为正；如果数据分布向左偏（负偏），偏度为负。

偏度大于0：右偏（Positive Skew），表示数据分布的尾部向右延伸，即数据向左侧偏离了中心，大部分数据位于均值右侧。
偏度小于0：左偏（Negative Skew），表示数据分布的尾部向左延伸，即数据向右侧偏离了中心，大部分数据位于均值左侧。
偏度接近0：数据相对对称分布。
绝对值大于 0：偏态。
绝对值大于 1：高度偏态。
绝对值0.5-1：中等偏态。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 蔡忠建. 对描述性统计量的偏度和峰度应用的研究[J]. 北京体育大学学报, 2009, 032(003):75-76.
[3] S.伯恩斯坦, R.伯恩斯坦, 伯恩斯坦,等. 统计学原理:描述性统计学与概率.上册[M]. 科学出版社, 2002.

建议反馈