规划求解

操作视频

# 1、作用

规划求解是研究约束条件下目标函数的极值问题的数学理论和方法。

# 2、输入输出描述

输入：目标函数，约束条件和未知数取值范围。
输出：规划求解结果，以及规划求解方程导出。

# 3、案例示例

某工厂生产甲、乙两种产品，每个产品的利润分别是 4000 和 3000 元。
生产甲产品需要用 A、B 机器加工，加工时间分布为每台 2 小时和 1 小时。生产乙产品需要用 A、B、C 三种机器加工。
加工时间为每台各一小时。若每天可以用于加工的机器时数为 A 是 10 小时，B 是 8 小时，C 是 7 小时。问该厂应生产甲、乙产品各几个，才能使总利润最大。可列出方程如下：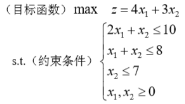

# 4、案例输入方法与操作

1：方程输入方法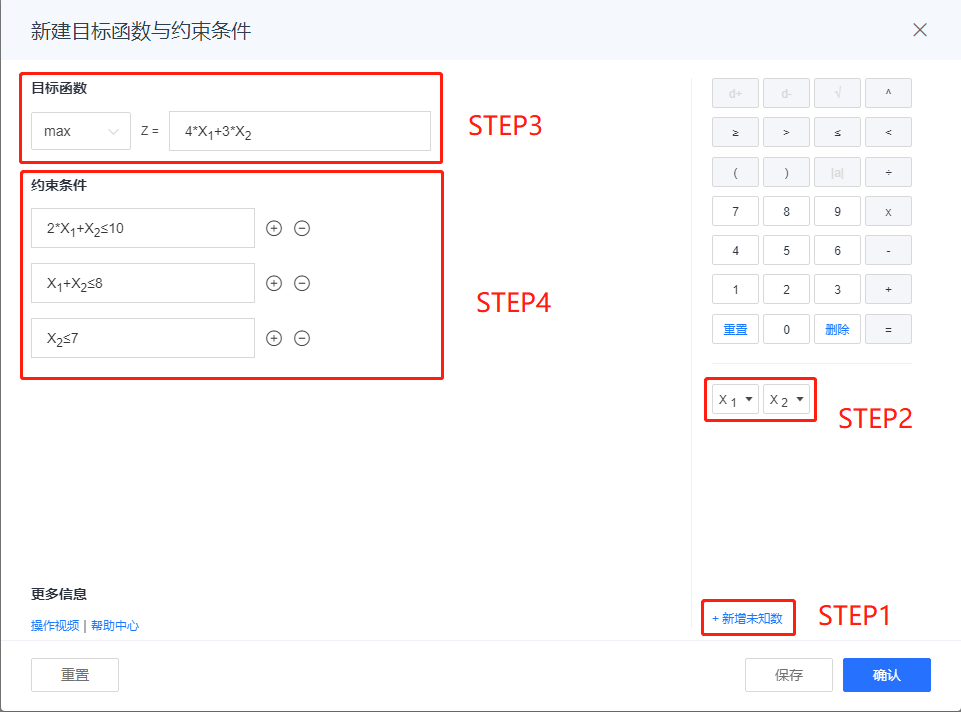

step1:添加未知数，本题有两个未知数，故最终应该添加为 x1 与 x2。
step2:在未知数选项中限定自变量的属性
取值范围，本题为 x1/x2 ＞ 0。

在取值范围选项中设定为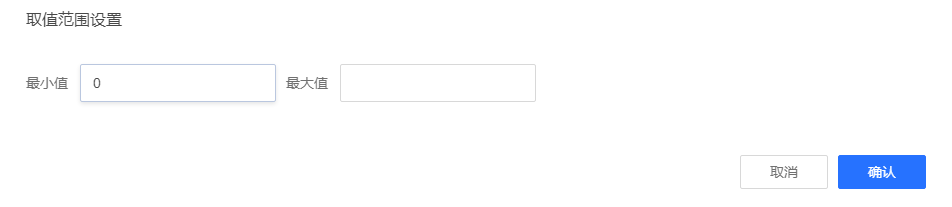

产品是不可分割的，故标识为整数：

step3:在按钮 2 输入目标函数 4x1+3x2
step4:在按钮输入约束条件如 2x1+x2<10
step5:如果输入错误可以重置，输入完成后点确认。
2：案例操作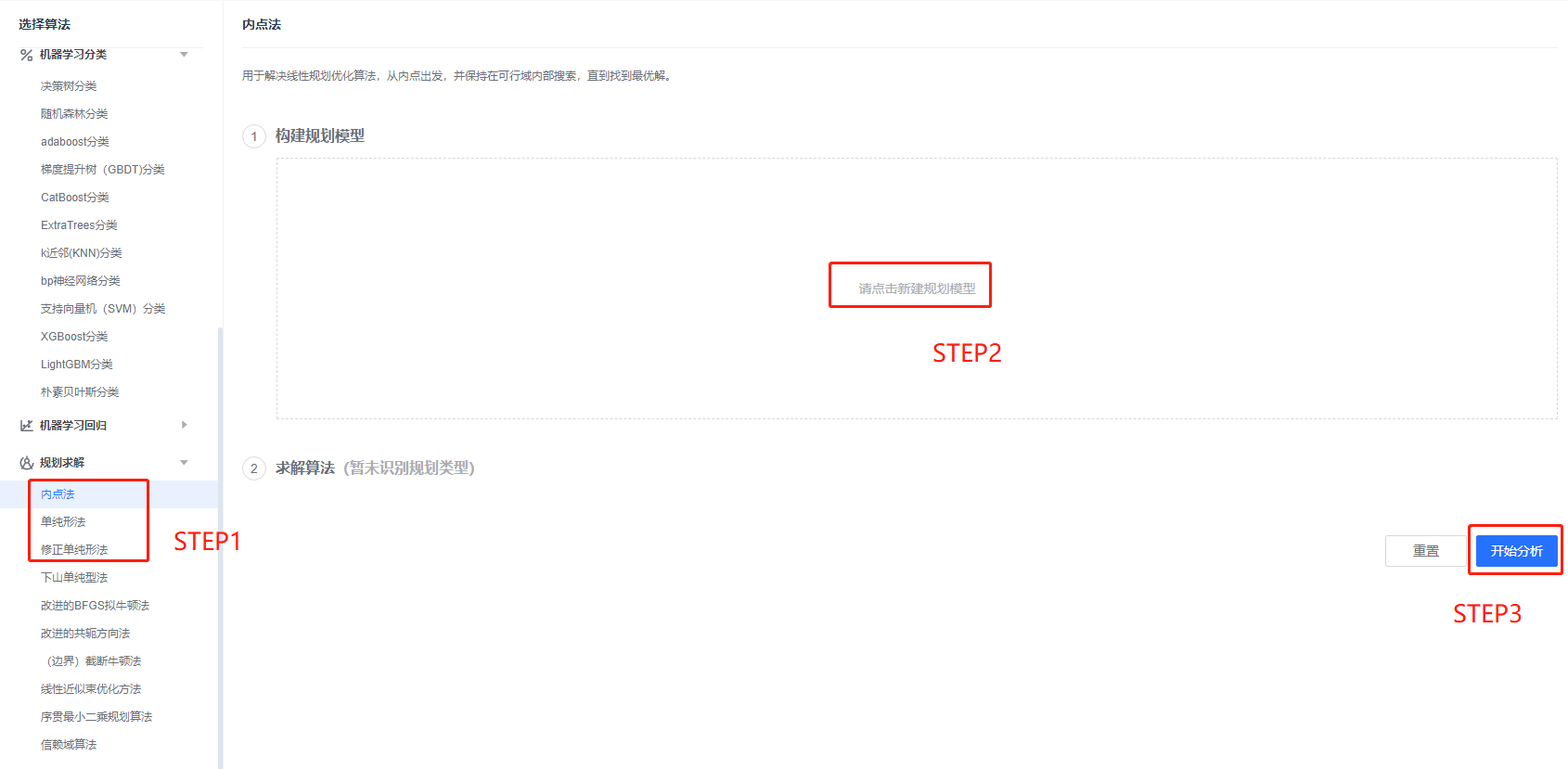

Step1：根据你的规划类型，选择求解器；
Step2：输入规划求解的方程(输入方法如上)；
Step3：点击分析

# 5、输出结果分析

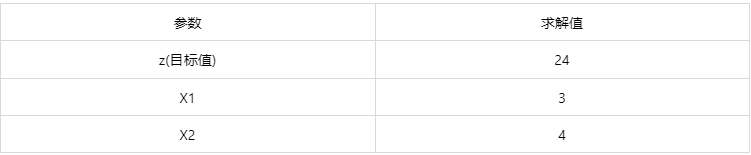
图表说明：上表展示规划求解的目标值与求解结果
智能分析：上表的结果为全局最优解，参数值供参考。
分析：结果为全局最优解，可以采用(不是则要选择其他求解器，或者检查输入的模型是否有问题)。可以认为甲产品生产 3 个，乙产品生产 4 个。

输出结果 2：规划求解模型

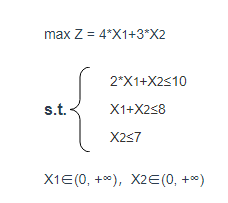
图表说明：上图展示规划求解的目标函数与约束条件

# 6、注意事项

如果选择的求解器无法使用，SPSSPRO 将自动跳转至可用的求解器。
不同规划类型对应的可用求解器：
线性规划：
- 内点法
- 单纯形法
- 修正单纯形法
- 线性近似约束优化方法
- 序贯最小二乘规划算法
- 信赖域算法
非线性规划：
- 边界约束条件问题：
  - 下山单纯性法
  - 改进的 BFGS 拟牛顿法
  - 改进的共轭方向法
  - 截断牛顿法
- 带有约束条件问题：
  - 线性近似约束优化方法
  - 序贯最小二乘规划算法
  - 信赖域算法

建议反馈